Пример 3.2.2. Применение общего уравнения динамики
Для механической
системы из предыдущего примера составить
дифференциальное уравнение движения
груза, воспользовавшись общим уравнением
динамики, а так же найти его решение.
Осевой момент инерции соосных блоков
полагать заданным. Будем также считать,
что в начальный момент грузу была
сообщена начальная скорость
,
направленная вниз.
РЕШЕНИЕ
На Рис. 6 изображена механическая система, внешние силы, действующие на нее, а так же силы и моменты сил инерции, препятствующие движению тел.
Дадим системе возможное перемещение в направлении, указанном стрелками. Составим выражение суммы работ всех этих усилий на соответствующих возможных перемещениях и приравняем его к нулю. Тогда
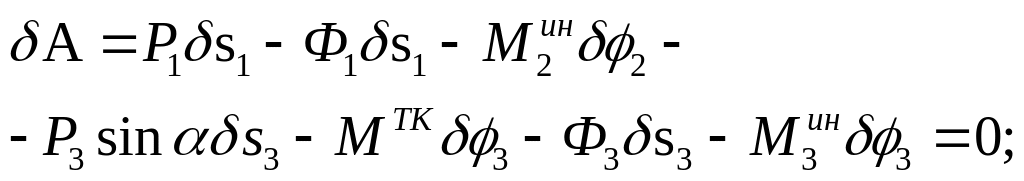
где
,
,
и
– силы и моменты сил инерции, приложенные
к соответствующим телам.
Уравнения кинематических связей остаются прежними:
.
Тогда, в силу голономности и стационарности связей системы, для возможных перемещений можно записать соотношения:
;
;
.
В выражении для суммы работ вынесем
за скобки, выражение в скобках приравняем
к нулю. Соотношения между линейными
ускорениями грузов и угловым ускорением
блоков аналогичны приведенным выше
(они получаются дифференцированием по
времени уравнений кинематических
связей).
Рис. 6
Выразим теперь ускорения тел системы через ускорение первого груза и вынесем его за скобки, содержащие инерционные усилия. После несложных преобразований, получим дифференциальное уравнение движения груза в виде:
,
где
– обобщенный инерционный коэффициент;
– обобщенная сила.
При получении
результата учтено, что осевой момент
инерции однородного диска
.
Для получения решения уравнения необходимо воспользоваться начальными условиями и формулой для равнопеременного движения:
.
Заметим, что если
и
(см. решение предыдущего примера), то
груз будет двигаться вниз равноускоренно.
При
,
груз будет двигаться вниз с постоянной
скоростью
.
Если
и
,
груз будет двигаться вниз равнозамедленно
до полной остановки.
Если
и
,
то груз начнет двигаться вниз
равнозамедленно до остановки, после
остановки начнется его равноускоренное
движение вверх.
Аналогичные
рассуждения можно провести для случая
.
При необходимости получить закон движения другого тела механической системы следует воспользоваться уравнениями кинематических связей.
Пример 3.2.3. Применение уравнения Лагранжа 2-го рода
Для механической системы из предыдущего примера составить дифференциальное уравнение движения груза, воспользовавшись уравнениями Лагранжа второго рода.
РЕШЕНИЕ
На Рис. 5 изображена механическая система и внешние силы, на нее действующие.
Воспользуемся уравнениями Лагранжа второго рода:
;
где
Составим выражение для кинетической энергии механической системы:
.
Запишем уравнения кинематических связей:
или
;
или
;
или
.
В формулу для кинетической энергии подставим угловые скорости вращения соосных блоков, диска и скорость центра масс диска, выраженные через скорость первого груза, тогда
.
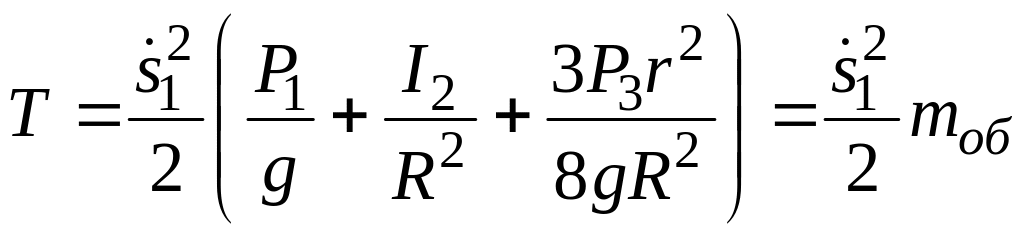При получении результата учтено, что осевой момент инерции однородного диска .
Возьмем соответствующие производные:
После несложных преобразований, получим дифференциальное уравнение движения груза:
,
где
;
.
Полученное уравнение совпадает с уравнением из предыдущего примера, его решение обсуждено выше.