3.2. Примеры решения заданий Пример 3.2.1. Применение принципа возможных перемещений
Найти величину
груза
при которой механическая система (Рис. 5),
состоящая из груза, двух соосных
(насаженных неподвижно на единую ось)
блоков и однородного диска, находится
в положении статического равновесия.
Вес диска, радиусы диска и блоков, угол
наклона плоскости
полагать
заданными величинами. При решении учесть
коэффициент трения качения диска
.
Качение происходит без проскальзывания.
Рис. 5
РЕШЕНИЕ
Рассматриваемая механическая система обладает одной степенью свободы.
Определим критическое состояние равновесия, соответствующее максимальному значению .
Предположим, система двигалась в направлении указанном стрелками (Рис. 5). При таком движении вес груза 1 настолько велик, что «перетягивает» все остальные тела системы. Уменьшая вес груза, приведем систему в состояние равновесия. Это и есть критическое состояние равновесия, соответствующее максимальному значению .
Учет трения качения осуществляется приложением к диску момента
,
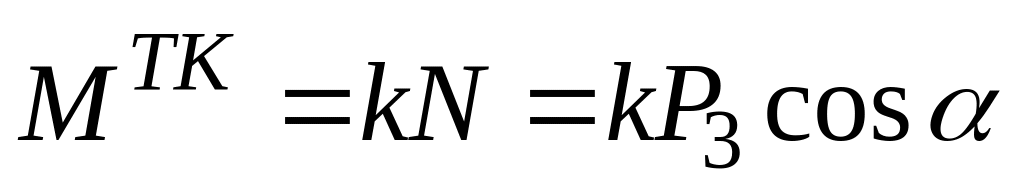препятствующего его вращению. Вычисление
его значения позволяет трактовать это
усилие как активное (задаваемое).
Наложенные связи оказываются идеальными
(реакции соосного блока приложены в
неподвижной точке, реакции диска – в
мгновенном центре скоростей, нити
нерастяжимы) и для получения условия
равновесия механической системы можно
воспользоваться принципом возможных
перемещений в форме (4).В рассматриваемом случае направления возможных перемещений точек и тел системы соответствуют стрелкам на Рис. 5, т.е. система имеет возможное движение только в этом направлении. Запишем выражение для суммы работ всех действующих сил на возможных перемещениях точек их приложения и приравняем 0.
Вынесем за скобку
.
Тогда
.
Запишем уравнения связей, используя соотношения кинематики
;
;
.
При записи учтено, что нити нерастяжимы, а мгновенный центр скоростей диска, катящегося без проскальзывания, расположен в точке его соприкосновения с плоскостью.
Для рассматриваемой механической системы (наложенные связи стационарны и голономны) возможные перемещения пропорциональны соответствующим скоростям, т.е. будут справедливы соотношения
;
.
Приравняв к нулю выражение в круглых скобках, получим выражение для расчета величины
,
при превышении которой механическая
система начинает движение в указанном
направлении:
.
Если предположить, что тела механической системы двигались в противоположном направлении, а затем вес груза увеличили так, чтобы система пришла в состояние равновесия, то это будет критическое состояние, соответствующее минимальному значению веса груза 1.
Применяя все предыдущие рассуждения и учитывая, что момент трения качения будет направлен в сторону, противоположную движению, для величины будет получено иное значение:
.
Таким образом, при
учете трения качения механическая
система будет находиться в покое при
любом значении веса груза, находящемся
в интервале
.
Аналогично решаются задачи при учете трения скольжения.