Задание 1. Применение метода кинетостатики для определения усилий в связях механической системы

1.1. Краткие сведения из курса механики Метод кинетостатики

Метод кинетостатики является обобщением принципа Даламбера для системы материальных точек:

в каждый момент времени главный вектор сил инерции уравновешивает главный вектор внешних сил; точно так же главный момент сил инерции относительно некоторого центра уравновешивает главный момент внешних сил.

Если действующие на -ю точку силы привести к равнодействующей внешних сил и равнодействующей внутренних сил , то, с учетом свойств внутренних сил (главный вектор и главный момент внутренних сил механической системы равны нулю), уравнения кинетостатики примут вид

(1)

где и – главный вектор и главный момент внешних сил, а и – главный вектор и главный момент сил инерции.

Принцип Даламбера дает удобный прием решения задач динамики несвободных систем. Путем приложения к точкам механической системы фиктивных сил инерции задача динамики легко сводится к соответствующей задаче статики. Уравнения (1) называют уравнениями кинетостатики. Для использования этих уравнений необходимо правильно вычислять главный вектор и главный момент сил инерции механической системы, в частности, твердого тела.

Так

• при поступательном движении тела

• при вращении тела вокруг неподвижной оси

• при плоском движении тела

где С – центр масс твердого тела.

Таким образом, для динамической задачи мы получили уравнения, которые можно трактовать как уравнения равновесия.

Если силы, действующие на точки механической системы, разделить на активные (задаваемые) и реакции связей, то уравнения (1) можно переписать в форме

(2)

где и – главные векторы активных сил, реакций связей и сил инерции соответственно, а – главные моменты этих сил, соответственно.

Заметим, что применение метода кинетостатики особенно удобно при известном (заданном или предварительно найденном) движении тел механической системы. В таком случае не представляет затруднений вычисление их ускорений и, как следствие, инерционных усилий, на них действующих. После этого неизвестные величины опорных реакций находятся из уравнений равновесия (2), записанных для тел, формирующих механическую систему.

Более подробно с материалом можно ознакомиться, например, в [1, 3, 4].

1.2. Пример решения задания

Механическая система¹, изображенная на Рис. 1, состоит из груза 1, двух соосных (насаженных неподвижно на единую ось) блоков, составляющих единое тело 2, и однородного диска 3. Вес груза , вес блоков , их радиусы и , а так же осевой момент инерции , вес диска и его радиус , коэффициент трения качения однородного диска k известны.

Для механической системы, изображенной на Рис. 1, найти реакции внешних и внутренних связей.

РЕШЕНИЕ

1. Мысленно расчленим механическую систему на три тела (груз 1, соосные блоки 2 и диск 3), приложив к каждому из тел соответствующие внешние силы и силы инерции (см. Рис. 1). Для описания равновесия тел механической системы запишем соответствующие уравнения:

2. Уравнения равновесия будут иметь вид

• для первого груза

;

• уравнения для соосных блоков

;

;

;

• уравнения для диска

;

;

.

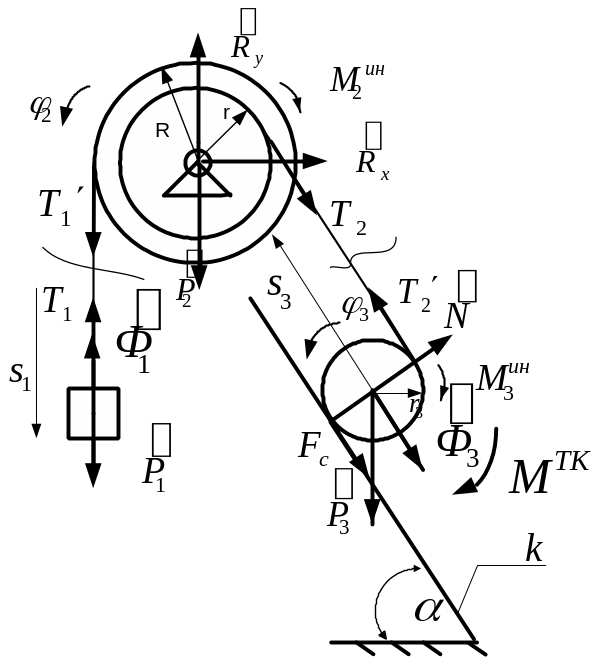
Рис. 1.

3. По аналогии с примером 3.2 из пособия [5], найдем ускорение движения груза в виде

,

где ;

.

4. Уравнения кинематических связей остаются прежними [5]:

.

5. Выразив скорости тел через скорость груза и продифференцировав эти выражения по времени, получим

.

6. Тогда силы и моменты сил инерции, приложенные к соответствующим телам, будут:

, , и .

7. Теперь алгебраические уравнения равновесия позволяют последовательно вычислить реакции внешних и внутренних связей:

;

;

;

;

.

С решением подобных примеров можно ознакомиться, например, в [2, 3, 4].