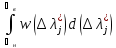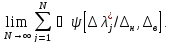-
Характеристики погрешностей результатов измерений.
Поскольку погрешности результатов измерений имеют случайный характер (случайные величины) для описания их свойств используются вероятностные характеристики (ВХ). Очевидно, что каждому измерительному эксперименту (результату измерений) соответствует погрешность ∆λϳ* (случайная величина). Упорядоченному множеству измерительных экспериментов {ИЭϳ}соответствует упорядоченное множество погрешностей {∆λϳ* }Nϳ=1,. Множество погрешностей {∆λϳ* }Nϳ=1 может порождаться соответствующим множеством средств измерений {СИϳ} Nϳ=1 или ограниченной совокупностью средств измерений {СИϳ} Nϳ=1 (п<N), но при выполнении ими последовательно во времени соответствующего числа измерений. Бесчисленное множество измерительных экспериментов {ИЭϳ} Nϳ=1 (ансамбль) порождает ансамбль погрешностей {∆λϳ*}∞ϳ=1. Ансамбль случайных величин - принятая в математической статистике модель, позволяющая построить систему определений вероятностных характеристик, представляющих ее свойства.
Существует два определения ВХ:
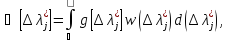 (21)
(21)
Где - область существования ∆λϳ*,
g[.]
– преобразование, лежащее в основе
определения ⊛[.],
w[.]
– плотность распределения вероятности
(.), и
- область существования ∆λϳ*,
g[.]
– преобразование, лежащее в основе
определения ⊛[.],
w[.]
– плотность распределения вероятности
(.), и
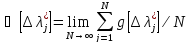 (22)
(22)
Наиболее
употребительны при описании свойств
погрешностей следующие три ВХ:
математическое ожидание (М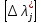 ),
дисперсия (D
),
дисперсия (D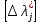 )
или связанное с ним среднее квадратическое
отклонение (D1/2
)
или связанное с ним среднее квадратическое
отклонение (D1/2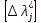 )
вероятность принадлежности погрешности
заданному интервалу [∆н,∆в]
(Р∆
[∆н,∆в]),
называемая в дальнейшем интервальной
вероятностью. Для них соотношения (21) и
(22) приобретают следующий вид:
)
вероятность принадлежности погрешности
заданному интервалу [∆н,∆в]
(Р∆
[∆н,∆в]),
называемая в дальнейшем интервальной
вероятностью. Для них соотношения (21) и
(22) приобретают следующий вид:
|
М |
(23) |
|
|
(24) |
|
D |
(25) |
|
|
(26) |
|
D1/2 |
(27) |
|
D1/2 |
(28) |
|
Р∆
[∆н,
∆в]
=
|
(29) |
|
Р∆
[∆н,
∆в]= |
(30) |
В
последнем соотношении
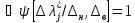 при
при
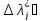 [∆н,
∆в]
и
[∆н,
∆в]
и
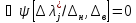 при
при
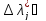 [∆н,
∆в].
[∆н,
∆в].
Поскольку
ВХ представляют свойства погрешностей,
именно к ним предъявляются требования,
которые должны выполняться при проведении
измерений. В метрологии установление
таких требований называется нормированием
характеристик погрешностей. Иначе
говоря, нормирование характеристик
погрешностей - установление для них
таких норм, выполнение которых обязательно
и гарантируется при выполнении измерений
с соблюдением оговоренных условий. Для
систематической погрешности и среднего
квадратаческого отклонения погрешности
такими нормами служат граничные
(предельно допустимые) значения Мдоп
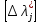 и Dдоп
1/2
и Dдоп
1/2
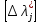 .
Для интервальной вероятности - установление
значения Р∆
[∆н,
∆в]
при допустимом интервале │∆н
- ∆в│≤
∆доп
или допустимое значение интервальной
вероятности при Р∆
[∆н,
∆в]≥
Р∆
доп
при фиксированном значении интервала
[∆н,
∆в].
.
Для интервальной вероятности - установление
значения Р∆
[∆н,
∆в]
при допустимом интервале │∆н
- ∆в│≤
∆доп
или допустимое значение интервальной
вероятности при Р∆
[∆н,
∆в]≥
Р∆
доп
при фиксированном значении интервала
[∆н,
∆в].
Нормирование характеристик погрешностей сопровождается указанием условий, соблюдение которых является необходимым для обеспечения выполнения требований, определяемых нормированием: свойства измеряемой величины, значения параметров внешней среды, длительность эксплуатации измерительного средства и т. п. Помимо характеристик погрешностей, нормироваться могут и другие метрологические характеристики (MX), к которым относятся любые характеристики объектов, процедур, средств и условий измерений, влияющие на точность получаемых результатов.
Примерами MX могут служить динамические характеристики входных воздействий, рабочие диапазоны средств измерений, характеристики преобразований, выполняемых измерительными модулями (импульсные переходные характеристики, разрядность квантователя, быстродействие и др.), характеристики условий измерений (температура, влажность, наличие аддитивных помех и др.). Так, установление уровня допустимых изменений входного воздействия на интервале измерений есть нормирование его динамических свойств, установление граничных значений влияющих факторов, определяющих т.н. нормальные условия измерений - нормирование характеристик условий.
Особую роль в обеспечении точности измерений играют характеристики преобразований, реализуемых измерительными модулями. Степень соответствия этих характеристик номинальным (идеальным) определяет вклад соответствующего преобразования в инструментальную погрешность. Вид требований, предъявляемых к соответствию реализуемых характеристик номинальным, зависит от вида соответствующих MX, а установление этих требований и составляет процедуру их нормирования.

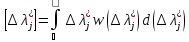 ,
,
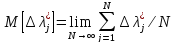 ,
,
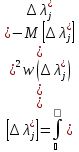
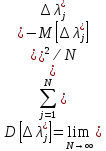 ,
,
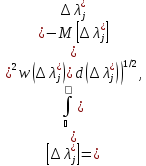
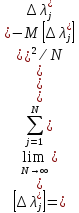 ,
,