1.2. Цифровые автоматы

В процессе обработки цифровой информации в электронных блоках интегральных датчиков могут возникнуть задачи обработки последовательностей дискретных сигналов во времени, которые нельзя решить с помощью одних комбинационных схем. Такие задачи имеют место в том случае, когда выходные сигналы устройств зависят не только от входных, поступающих в данный момент, но и от всех предыдущих сигналов, поступивших ранее. Подобные задачи решают цифровые автоматы с памятью.

Рассмотрим элементарные цифровые автоматы, роль которых выполняют триггеры. Триггеры представляют собой логические цепи с памятью и являются основной элементной базой для построения любых сколь угодно сложных цифровых устройств. Существуют несколько типов триггеров. В первую очередь их разделяют на тактируемые и нетактируемые. В нетактируемых триггерах их состояния изменяются сразу, как только установятся сигналы на входах, а в тактируемых изменение выходных сигналов осуществляется в соответствии с входными только после того, как будут поданы разрешающие сигналы на их тактовые входы.

Тактирование триггеров возможно посредством статической и динамической синхронизации. Статическая синхронизация осуществляется импульсом (логическим уровнем), а динамическая - фронтом (логическим перепадом 1/0 или 0/1). В обобщенном виде блок-схема триггера показана на рис. 3, а.

В состав триггеров входят комбинационные управляющие схемы и бистабильные запоминающие ячейки. Триггер может иметь несколько входов: 1, 2, 3 и т.д. и два выхода - прямой и инверсный. Каждый из входов в различных типах триггеров имеет свое функциональное назначение. Обозначение входов триггеров принято на левом поле их условного изображения в виде букв латинского алфавита:

S - вход принудительной раздельной установки триггера в состояние q = 1;

R - вход принудительной раздельной установки триггера в состояние q = 0;

D - информационный вход для установки в одно из состояний (q = 1 или q = 0) в триггерах задержки;

J - вход тактированной установки в состояние q = 1 в универсальных триггерах;

K - вход тактированной установки в состояние q = 0 в универсальных триггерах;

Т - счетный вход;

С - вход синхронизации.

Управляющие и информационные входы триггеров могут быть как прямыми, так и инверсными. Одноименных входов в одном и том же триггере может быть несколько. В этом случае их объединяют логическими операциями конъюнкции или дизъюнкции.

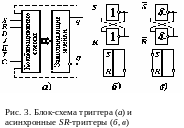SR-триггер. Наиболее простым и распространенным из всех типов триггеров является триггер с установочными входами, или так называемый SR-триггер. Схемная реализация этого триггера может быть осуществлена в виде бистабильной дизъюнктивной или конъюнктивной ячейки (рис. 3, б, в). Выходные сигналы у SR-триггера могут принимать значения 0 или 1 в зависимости от сочетания сигналов на его входах.

В табл. 7 и 8 представлены переходы дизъюнктивной и конъюнктивной бистабильных ячеек из текущих состояний qt в очередные, желаемые состояния qt+1 под воздействием входных сигналов S и R. Очередные состояния записаны в клетках на пересечении строк и столбцов.

Таблицы переходов триггеров записывают в форме матриц Карно, что позволяет сравнительно просто получать минимальные выражения функций переходов.

Функции переходов триггеров называют характеристическими уравнениями, которые определяют общий закон функционирования. Однако для однозначного построения принципиальных схем триггеров таблиц переходов недостаточно (исключение составляют бистабильные ячейки SR), так как триггер с одним и тем же законом функционирования может быть построен по одноступенчатой схеме, двухступенчатой, синхронизируемой импульсом или фронтом и т.д. Принципиальные схемы при этом будут различными.

Таблица 7. Таблица 8.

Для дизъюнктивной бистабильной ячейки из табл. 7 характеристическое уравнение запишется в следующем виде:

.

Аналогично из табл. 8 запишется характеристическое уравнение для конъюнктивной бистабильной ячейки:

.

Для дизъюнктивной ячейки сочетание двух нулей на входах является режимом хранения, а сочетание двух единиц запрещено, так как, например, при переходе от двух единиц на входе к двум нулям триггер может принимать неопределенное состояние (0 или 1). В результате устройство, спроектированное с использованием запрещенного состояния, становится неработоспособным.

Для осуществления переходов триггера из одного состояния в другое на его входах должны быть противоположные сигналы, т.е. всегда между сигналами на входах должно выполняться соотношение SR = 0. При объединении соседних единиц в матрице Карно неопределенные состояния могут трактоваться как единичные.

Функционирование конъюнктивной бистабильной ячейки осуществляется аналогично, с той лишь разницей, что сигналы на ее входах должны быть инверсными. SR-триггер входит во все типы триггеров в качестве выходного.

Классическая задача синтеза триггера сводится к определению комбинационной схемы, управляющей выходным триггером. Каждая ступень рассматривается отдельно. Причем к входным сигналам управляющей комбинационной схемы добавляются сигналы, поступающие по цепям обратной связи с выходов основного триггера (на рис. 3, а обратные связи показаны пунктиром). Выходные сигналы управляющей комбинационной схемы являются входными для возбуждения входов основного триггера. Синтез триггера осуществляется в несколько этапов:

1. По таблицам переходов синтезируемых триггеров составляют таблицы возбуждения входов S и R основного триггера.

2. По таблицам возбуждения определяют минимальные логические выражения отдельно для функций S и R.

3. По найденным функциям S и R строят принципиальную схему комбинационной части триггера, в которой входы для цепей обратной связи соединяют с выходами основного триггера, а выходы комбинационной схемы подключают ко входам S и R основного триггера.

Используя приведенные ранее правила, рассмотрим синтез схем наиболее распространенных триггеров.

Таблица 9

SCR-триггер. Словесное описание функционирования триггера следующее: “Синтезировать схему одноступенчатого SCR-триггера, тактируемого импульсом и переключающегося в соответствии с бистабильной SR-ячейкой”. В табл. 9 приведены переходы для SCR-триггера, записанные на основе словесного описания. По табл. 9 находим характеристическое уравнение SCR-триггера

(7)

и раздельные таблицы возбуждения входов выходного триггера (табл. 10 и 11).

Таблица 10. Таблица 11

Из таблиц возбуждения определяем логические выражения для функций S и R:

(8)

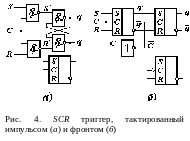
Принципиальная схема и условное графическое изображение SCR-триггера, построенного по уравнениям (7) и (8), приведены на рис. 4, а. Реализация динамического режима SCR-триггера возможна за счет усложнения его принципиальной схемы. На рис. 4б представлена схема двухступенчатого триггера, описываемая теми же уравнениями (7) и (8), синхронизируемого одной импульсной последовательностью. Причем первая и вторая ступени синхронизируются импульсами разной полярности, т.е. на первую ступень импульсы подаются непосредственно, а на вторую - через инвертор.

Возможность синхронизации фронтом импульса достигается тем, что в первой ступени переключения осуществляются по перепаду синхроимпульса 0/1, а во второй ступени в этот момент переключения отсутствуют, т.е. вторая ступень не реагирует на изменения состояний в первой ступени. И только при окончании действия синхроимпульса (при перепаде 1/0) информация с выходов первой ступени переписывается на выходы второй ступени, на выходах же первой ступени информация остается неизменной. Таким образом, в идеальном случае время полного цикла переключений двухступенчатых триггеров равно длительности синхроимпульса. В реальных случаях к этому времени добавляется время задержки при прохождении сигналов через логические элементы.

D-триггер. Словесное описание функционирования следующее: “Синтезировать триггер с одним информационным входом, перепись информации в котором со входа на выход осуществляется по приходу синхроимпульса”.

В табл. 12, 13 и 14 приведены переходы и состояния возбуждения выходного триггера, по которым определены следующие функции:

(9)

Таблица 12 Таблица 13 Таблица 14

На рис. 5 изображена принципиальная схема, реализованная по функциям (9). D-триггер не имеет неопределенных состояний. Его схема может быть также выполнена двухступенчатой с синхронизацией фронтом.

JCK-триггер отличается от SCR-триггера наличием перекрестных цепей обратной связи с выходов основного триггера на входы комбинационной части (рис. 6).

Таблица 15 Таблица 16

Из табл. 15 и 16 находим функцию переключения и функции возбуждения входов выходного триггера:

Синтез двухступенчатых триггеров осуществляется аналогично синтезу одноступенчатых. На рис. 7, а приведена обобщенная блок-схема двухступенчатого триггера, а на рис. 7, б - его принципиальная схема, построенная по тем же уравнениям, что и для одноступенчатого. Схема универсального триггера дополнена асинхронными входами и для принудительной установки триггера в начальное состояние.

Универсальный JCK-триггер кроме описанных ранее режимов может работать в счетном режиме, т.е. триггер откликается изменением выходных состояний на каждый перепад логических сигналов 0/1 на входе С.

Рис. 7. Блок-схема двухступенчатого триггера (а) и универсальный JCK-триггер (б)

Все рассмотренные типы триггеров могут применяться в интегральных датчиках в качестве запоминающих ячеек для построения цифровых автоматов обработки измерительной информации. Интегральные датчики в совокупности с цифровыми автоматами представляют собой сложные интеллектуальные приборы.

Цифровым автоматом с памятью называется преобразователь дискретной информации, способный переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы, функционально зависящие от входных сигналов и сигналов внутренних состояний. Наличие памяти в цифровом автомате позволяет иметь множество внутренних состояний, которые определенным образом влияют на выходные сигналы. Во всех реальных автоматах число внутренних состояний является конечным. Входные сигналы X(t), выходные сигналы Y(t) и сигналы внутренних состояний А(t) представляются в цифровых автоматах, как правило, в двоичном коде. Преобразование входных сигналов в выходные в цифровых автоматах осуществляется последовательно во времени, поэтому их называют последовательностными автоматами. Главным отличием последовательностных автоматов от комбинационных устройств является то, что одним и тем же входным сигналам могут соответствовать различные входные сигналы, что определяется очередностью смены внутренних состояний.

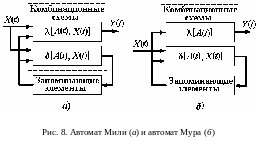
Цифровые автоматы с памятью разделяются на синхронные и асинхронные (рис. 8). В синхронных автоматах смена сигналов внутренних состояний и выходных сигналов тактируется специальным тактовым генератором. Каждый такт работы такого автомата представляет собой дискретное время и определяется порядковым номером, считая от начальной отметки. В асинхронных автоматах смена сигналов внутренних состояний и выходов может происходить только при изменении входных сигналов.

Процесс работы как синхронных, так и асинхронных автоматов может быть определен двумя функциями: функцией переходов и функцией выходов:

, , (10)

где  - функция переходов;  - функция выходов; t - текущий дискретный момент времени; (t + 1) - очередной дискретный момент времени.

Цифровые автоматы, описываемые функциями вида (10), называют автоматами Мили (рис. 8, а). Другим типом цифровых автоматов являются автоматы, у которых в функцию выходов в явном виде не входят входные сигналы:

, . (11)

Автоматы, описываемые функциями вида (11), называют автоматами Мура (рис. 8, б). Автоматы Мура, хотя и имеют принципиальные отличия от автоматов Мили как по структурной организации, так и по характеру работы, могут рассматриваться как частный случай автоматов Мили, так как их всегда можно представить в виде

, .

Между автоматами Мили и Мура существует взаимно-однозначное соответствие, т.е. от автомата Мили, выполняющего определенные функции, можно перейти к автомату Мура с такими же функциями и наоборот. Аппаратная реализация автоматов Мили и Мура разная. Автоматы Мили требуют меньшего объема памяти, однако они имеют более сложные комбинационные схемы логических преобразований.

Для построения структурной схемы цифрового автомата необходимо иметь исходную информацию о законе его функционирования, который накладывает требования на используемые ячейки памяти и законы изменения информации в этих ячейках. Исходной информацией об автомате чаще всего служат словесные описания или временные диаграммы, на основе которых намечается число внутренних состояний, желаемые входные сигналы и соответствующий этим сигналам порядок изменения состояний памяти. Существуют несколько различных способов описания работы цифровых автоматов, из которых наибольшее распространение получили два: графический и табличный. В общем случае переход от словесных описаний к таблицам или графам осуществляется на основе специального математического аппарата (алгебры событий), требующего сложных формальных преобразований. На практике вместо сложных преобразований используют различные эвристические приемы, которые позволяют быстрее получить хорошие результаты.

Графы автоматов задают с помощью вершин и дуг. Вершины обозначают кружками, внутри которых ставят номер состояния или его кодированное значение, т.е. вершины соответствуют состояниям, а дуги - переходам. Дуги изображают в виде направленных стрелок между вершинами. Для автоматов Мили дуги помечают кодами входных сигналов и через запятую - выходных сигналов, а код выходных сигналов записывают рядом с вершинами, так как в автоматах Мура внутренние состояния соответствуют выходным сигналам в данный момент времени.

Пример 1. Задать автомат для последовательного двоичного сумматора со следующим словесным описанием работы: “Построить цифровую схему для суммирования двух последовательных двоичных чисел, в которой сумма очередных двух разрядов должна складываться с результатом переноса от предыдущего сложения. Результат сложения должен быть передан на выход в последовательном коде, соответствующем суммарному”. При аппаратном сложении, так же как и при сложении “столбиком на бумаге”, могут быть два случая: 1) переноса нет, при этом должен быть установлен нуль; 2) перенос есть, необходимо установить единицу. Таким образом, память в автомате должна иметь два состояния: для изображения нуля и для изображения единицы (на графе рис. 24, а это две вершины). Входные сигналы X₁(t) и X₂(t) могут иметь четыре сочетания: 00, 01, 11, 10.

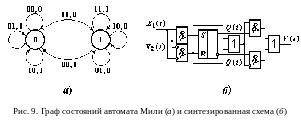
Дуги - переходы из одного состояния в другое и наоборот помечают кодом входных сигналов. Значения выходного сигнала от результата суммирования могут быть 0 или 1. Эти значения также приписывают дугам графа через запятую, стоящую после значений входных сигналов.

Графы автоматов дают наглядное представление о его структуре, однако для аналитического описания схемы удобнее пользоваться табличным способом задания автоматов. Целью табличного способа задания автоматов является сведение описания его схемы к языку алгебры логики. Цифровой автомат считается полностью определенным, если известны входные и выходные коды, аналитические функции переходов  и выходов , начальные значения состояний и аналитические функции возбуждения входов, примененных ячеек памяти. Перед синтезом автомата входные и выходные коды обычно заданы, а выбор ячеек памяти осуществляют из условий оптимизации схемы, а также из условий согласования сигналов с другими логическими элементами.

По графу работы цифрового автомата строят таблицы переходов и выходов, т.е. две разные таблицы. Причем строки обеих таблиц помечают кодом текущих состояний, а столбцы - кодом входных сигналов. В таблице переходов (табл. 25) для рассмотренного случая в клетках на пересечениях строк и столбцов записывают код очередных состояний, в которые переходит автомат из текущего состояния, соответствующего данной строке, под воздействием входных сигналов, соответствующих данному столбцу.

Таблица 17 Таблица 18

A(t)	X1 X2					A(t)	X1 X2
	00	01	11	10			00	01	11	10
0	0	0	1	0		0	0	1	0	1
1	0	1	1	1		1	1	0	1	0

В таблице выходов (табл. 18) на пересечении строк и столбцов в клетки записывают код выходных сигналов. В данном случае код одноразрядный, но в общем случае он может быть n-разрядным.

Пример 2. Словесное описание работы автомата: “Синтезировать схему цифрового устройства для сравнения двух последовательных двоичных чисел X₁ и X₂, начиная со старших разрядов”. Устройство должно иметь три выхода. На первом выходе Y₁ должен появиться единичный сигнал в случае равенства чисел при X₁ = X₂, на втором - при X₁  X₂ и на третьем - при X₁  X₂. Автомат должен быть выполнен по типу автомата Мура. Граф работы автомата представлен на рис. 10, а.

Автомат должен иметь три состояния и три разных выходных сигнала. В автомате Мура выходные сигналы соответствуют состояниям переходов, а граф имеет три вершины. Кодирование состояний может быть следующим:

A₁(t) = Y₁(t) = 100 при X₁ = X₂,

A₁(t) = Y₁(t) = 010 при X₁  X₂,

A₁(t) = Y₁(t) = 001 при X₁  X₂.

Входные сигналы разрядов сравниваемых чисел и могут иметь следующие значения: 00, 01, 11, 10. Таблица переходов автомата совмещается с таблицей выходов (табл. 19). Верхний индекс у входных сигналов соответствует номеру анализируемого разряда. Таблицы переходов и выходов содержат полную информацию для определения функций переходов и выходов в виде булевых выражений.

Таблица 19

A=Y
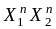
	00	01	11	10
100	100	001	010	100
010	010	010	010	010
001	001	001	001	001

После определения кодированных таблиц переходов и выходов начинается этап структурного синтеза автоматов, заключающийся в определении аналитических функций переходов и выходов. Прежде всего выбирают тип триггеров, используемых в качестве запоминающих устройств, и их необходимое число, которое определяют по следующей формуле:

, (12)

где n - необходимое число триггеров; N - число внутренних состояний автомата. Полученное значение триггеров округляют до ближайшего целого числа в большую сторону. Триггеры, необходимые для реализации свойств памяти проектируемых цифровых автоматов, представляют собой элементарные автоматы.

Сложные цифровые автоматы чаще всего выполнены из наборов элементарных автоматов, связанных между собой комбинационными схемами. Элементарные автоматы (триггеры) имеют следующие особенности:

1) являются автоматами Мура, так как их состояния совмещаются с сигналами выходов;

2) имеют минимум состояний, т.е. два устойчивых внутренних состояния и соответственно два значения выходных сигналов: 0 или 1;

3) могут иметь один или несколько входов, по сигналам на которых автоматы переходят из одного состояния в другое и наоборот.

В качестве элементарных автоматов, как правило, используют D-, Т-, SR- и JCK-триггеры. В табл. 20 приведены для перечисленных типов триггеров значения входных сигналов, переводящих их из одного состояния в другое. Для возбуждения переходов триггеров на их входы подаются сигналы, которые в общей схеме проектируемых цифровых автоматов зависят от входных сигналов всего автомата и от состояний выходов всех триггеров, применяемых в автомате.

Таблица 20

Q(t)  Q(t+1)	D	T	SR	JCK
0  0	0	0	0	0
0  1	1	1	10	1
1  0	0	1	01	1
1  1	1	0	0	0

Сигналы возбуждений триггеров определяют в виде аналитических функций возбуждения в следующем виде:

(13)

где q(t) - обобщенное обозначение входа триггера (для D-триггеров q(t) = D(t), для Т-триггеров q(t) = Т(t) и т.д.).

Для аналитического построения функций возбуждения составляют специальные таблицы по таблицам переходов конкретных автоматов. Опишем порядок составления таких таблиц для примера 1 синтеза последовательного сумматора. Ниже приведены таблицы возбуждения для последовательного сумматора на разных типах триггеров (для D-триггера - табл. 21для T-триггера - табл. 22, для SR-триггера – табл. 23, для JCK-триггера - табл. 24).

Таблица 21 Таблица 22

A(t)	X1 X2					A(t)	X1 X2
	00	01	11	10			00	01	11	10
0	0	0	1	0		0	0	0	1	0
1	0	1	1	1		1	1	0	0	0

Таблица 23 Таблица 24

A(t)	X1 X2					A(t)	X1 X2
	00	01	11	10			00	01	11	10
0	0,-	0,-	1,0	0,-		0	0,-	0,-	1,-	0,-
1	0,1	-,0	-,0	-,0		1	-,1	-,0	-,0	-,0

При заполнении табл. 21 - 24 в клетки на пересечениях строк и столбцов вписывают значения входных сигналов, переводящих триггер в соответствие с таблицей переходов. Значения входных сигналов в табл. 21 - 24 определяют по табл. 20, являющейся при этом вспомогательной. Далее внутренние состояния А(t) приравнивают к состояниям выходов используемых триггеров, т.е. считают, что А(t) = Q(t). В соответствии с табл. 21 - 24 аналитические выражения функций возбуждения записаны в табл. 25.

Таблица 25

Тип триггера	Функция возбуждения
D
Т
SR
JCK

Функции выходов определяют на основании таблиц выходов. Так, для примера последовательного сумматора, функцию выходов запишем в виде

.

Любой цифровой автомат может быть реализован как по типу автоматов Мили, так и по типу автоматов Мура. При этом может оказаться, что автоматы различных типов, но выполняющие одни и те же функции, отличаются аппаратными затратами, быстродействием и другими техническими характеристиками. Поэтому при проектировании автоматов необходимо отдавать предпочтение оптимальным аппаратным решениям. В некоторых компромиссных случаях определяющим фактором являются не аппаратные затраты, а, например, быстродействие или использование иной элементной базы.

Правила замены автоматов Мили автоматами Мура

1. Таблицы переходов и выходов автоматов Мили совмещают, и каждой отличающейся паре внутри этих таблиц присваивают очередной номер N, начиная с нулевого. Причем одинаковым парам переходов и выходов должен соответствовать одинаковый номер. Номер записывается в тех же клетках через черту (табл. 26, построенная для примера 1 последовательного сумматора).

Таблица 26 Таблица 27

A(t)	X1 X2					A(t)	X1 X2
	00	01	11	10			00	01	11	10
0	0,0/0	0,1/1	1,0/1	0,1/1		0	0	1	2	1	0
1	0,1/1	1,0/2	1,1/3	1,0/2		1	0	1	2	1	1
						2	1	2	3	2	0
						3	1	2	3	2	1

2. В новой табл. 27 автомата Мура каждый номер N считается внутренним состоянием A(t), и в клетках таблицы ему приписываются такие внутренние состояния и состояния выходов, какие имели место в таблице переходов Мили при всех возможных сочетаниях X₁ и X₂.

Правила замены автоматов Мура автоматами Мили

1. В каждую клетку таблицы переходов автомата Мура вписывают, через запятую, символы состояний выходов Y, соответствующие состояниям переходов.

2. Полученную таблицу необходимо минимизировать, объединяя совместные состояния.

Пример преобразования автоматов Мура к автоматам Мили показан в табл. 28 и 29.

Таблица 28 Таблица 29

A(t)	X1 X2					A(t)	X1 X2
	00	01	11	10			00	01	11	10
0	0,0	1,1	2,0	1,1		0	0,0	0,1	1,0	0,1
1	0,0	1,1	2,0	1,1		1	0,1	1,0	1,1	1,0
2	1,1	2,0	3,1	2,0
3	1,1	2,0	3,1	2,0

В табл. 29 при минимизации совмещены состояния 0 и 1, а также состояния 2 и 3.

В заключение рассмотрим синтез реверсивного синхронного счетчика для интегрирования частотных сигналов датчиков с целью получения, например, скорости по непрерывным измерениям ускорений. Задача синтеза - теоретически определить комбинационные цепи, связывающие входы и выходы всех триггеров проектируемого счетчика. В качестве исходных данных для счетчика должны быть указаны: тип счетчика - синхронный или асинхронный; коэффициент пересчета счетчика или его разрядность; код, в котором должен работать счетчик; тип триггеров, на которых должен быть построен счетчик. Режим работы реверсивного счетчика (суммирование или вычитание) определяется цепями связи счетных входов последующих триггеров с выходами предыдущих по правилу: если передача осуществляется с прямых выходов на входы следующих, то реализуется режим суммирования, при передаче сигналов с инверсных выходов реализуется режим вычитания. В схемах это достигается использованием коммутаторов, управляемых сигналом знакового входа. При проектировании счетчика возможно рассмотрение одного любого режима, а дополнение функции реверсивности возможно простым применением коммутатора.

По заданному коэффициенту пересчета счетчика определяют число триггеров, необходимых для его реализации. После определения числа триггеров по заданному коду счетчика составляют таблицу функционирования, в которой для каждого состояния счетчика (начиная с нулевого) последовательно отмечают состояния выходов триггеров. В таблице функционирования против каждого состояния счетчика в данный момент указывают его состояние в следующий момент, т.е. очередное состояние (табл. 30).

По таблице функционирования для каждого очередного состояния , , , определяют функции переходов.

Таблица 30

№	Текущие состояния				Очередные состояния
0	0	0	0	0	0	0	0	1
1	0	0	0	1	0	0	1	0
2	0	0	1	0	0	0	1	1
3	0	0	1	1	0	1	0	0
4	0	1	0	0	0	1	0	1
5	0	1	0	1	0	1	1	0
6	0	1	1	0	0	1	1	1
7	0	1	1	1	1	0	0	0
8	1	0	0	0	1	0	0	1
9	1	0	0	1	1	0	1	0
10	1	0	1	0	1	0	1	1
11	1	0	1	1	1	1	0	0
12	1	1	0	0	1	1	0	1
13	1	1	0	1	1	1	1	0
14	1	1	1	0	1	1	1	1
15	1	1	1	1	0	0	0	0

Для упрощения записей выполним единичные конъюнкции (минтермы) всех состояний счетчика:

. (14)

Функции переходов для очередных состояний триггеров через минтермы (14) запишутся в следующем виде:

(15)

После составления функций переходов осуществляют их минимизацию. Для этого используют топологические карты Карно (рис. 11).

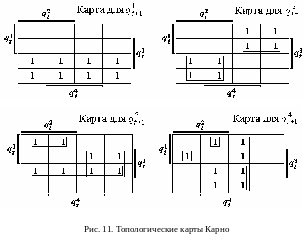
С помощью карт Карно функции переходов (16) упрощаются:

(17)

Для определения логических схем возбуждения входов триггеров необходимо каждую из минимизированных функций переходов (17) решить совместно с характеристическим уравнением триггера, примененного в данном разряде счетчика. Так, для универсального JCK-триггера при наличии синхроимпульса характеристическое уравнение имеет вид

(18)

где i - номер разряда счетчика, в котором применен данный триггер.

При использовании JCK-триггера применительно к построению четырехразрядного синхронного двоичного счетчика совместное решение уравнений (17) и (18) дает возможность соединить выходы предыдущих триггеров со входами последующих. В синхронном счетчике входы синхронизации С всех триггеров должны быть соединены вместе и синхроимпульсы должны подаваться на все триггеры одновременно. Принципиальная схема синхронного двоичного счетчика, построенного на основе соотношений (17 и 18), представлена на рис. 12.

Разрядность счетчика может наращиваться аналогичными тетрадами до требуемого значения. Счетчики оснащаются также схемами предварительной записи начальных данных (на рис. 12 не показаны). В интегральных датчиках реверсивные счетчики нашли широкое применение в качестве интеграторов частотных сигналов. Практически для частотных сигналов они представляют идеальные интеграторы, на выходе которых имеет место цифровой код, готовый для восприятия ЭВМ.