1. Логическое проектирование цифровых устройств

1.1. Комбинационные схемы

Комбинационными устройствами называют логические устройства, не имеющие в своем составе запоминающих ячеек, при этом выходные сигналы зависят от входных, имеющих место только в данный момент времени.

Синтез логического устройства представляет собой процесс построения принципиальной схемы по заданному словесному или математическому описанию работы устройства. Все цифровые устройства оперируют двоичными кодами, т.е. наборами нулей и единиц. Для описания цифровых устройств используется алгебра логики, в которой так же, как и в двоичном кодировании, переменные могут принимать только два значения: 0 или 1. В алгебре логики имеются три элементарных действия: дизъюнкция, конъюнкция и инверсия.

Дизъюнкция, или логическое сложение, выполняется по следующим правилам: 0V0 = 0, 0V1 = 1, 1V0 = 1, 1V1 = 1, где V - знак операции дизъюнкции. Можно также пользоваться знаком “+”, но в логических выражениях этот знак читается как ИЛИ. В дизъюнкции, в отличие от двоичного кодирования, при суммировании двух логических единиц переносов не осуществляется.

Конъюнкция, или логическое умножение, осуществляется по следующим правилам: 00 = 0, 01 = 0, 10 = 0, 11 = 1, где  - знак операции конъюнкции. В логических выражениях допустимо также условное изображение операции конъюнкции - отсутствие какого-либо знака между переменными, записанными без пробела, читается это как И.

Инверсия представляет собой отрицание истины. Например, инверсия единицы есть нуль, а инверсия нуля есть единица. Операция инверсии обозначается прямой чертой над переменной: (читается: не икс, не нуль, не единица).

Законы алгебры логики - это комбинации из дизъюнкций, конъюнкций и инверсий над логическими переменными и возможные соотношения между ними.

Законы отрицания в виде функций Пирса и Шеффера являются полными, т.е. посредством этих функций можно описать работу любого сколь угодно сложного логического устройства. Число различных логических функций от n переменных определяется соотношением N = 22n.

В цифровых автоматах выходные сигналы зависят от входных, имеющих место не только в данный момент времени, а также от того, какие сигналы присутствовали на входах и выходах в предшествующие моменты времени. Для запоминания различных сигналов применяют триггерные ячейки памяти.

Основные законы алгебры логики описаны в табл. 1.

Для двух переменных имеют место 16 логических функций, математические соотношения и графические обозначения которых приведены в табл. 2.

Графическое изображение логических элементов осуществляется в виде прямоугольников, внутри которых ставятся условные символы:  - элементы с выполнением операции конъюнкции; 1 - элементы с выполнением операции дизъюнкции; =1 - исключающее ИЛИ; n - мажоритарный элемент.

Таблица 1

Название	Выражение
Закон универсального множества	1VX1VX2VX3… VXn = 1
Закон нулевого множества	0X1X2X3… Xn = 0
Законы повторения	XVXVXVX… VX = X XXXX… X = X
Закон многократной инверсии	и т.д.
Переместительный закон	X1VX2 = X2VX1, X1X2 = X2X1
Сочетательный закон	X1(X2X3) = (X1X2)X3 = X2(X1X3)
Законы дополнительности
Распределительные законы	X1X2VX3 = (X1VX2)(X2 VX3) X1VX2 X3 = (X1X2)V(X2 X3)
Законы поглощения	X1X1VX2 = X1, X1X1X2 = X1
Законы склеивания	X1X2VX1 =X1 (X1X2)V( ) =X1
Законы отрицания: Пирса Шеффера
Законы Блека - Порецкого

С левой стороны прямоугольников изображают входы, а с правой - выходы. Входы или выходы, помеченные кружочками, соответствуют инвертированию сигнала. Входы или выходы, не несущие логической информации, например, входы расширения или питания помечают крестиком . На основе логических элементов может быть построена электронная схема любой сложности. Все электронные схемы с логическими элементами условно можно разделить на два типа: комбинационные устройства и цифровые автоматы.

Переключательной функцией в алгебре логики называют функцию, представляющую собой зависимость выходного сигнала от входных, имеющих место в данный момент времени. Переключательные функции чаще всего составляют в совершенной дизъюнктивной нормальной форме (СДНФ). В свою очередь, СДНФ - это логическая сумма элементарных конъюнкций на всех входных переменных, соответствующих единичным состояниям выходного сигнала. Причем в элементарные конъюнкции должны входить по одному разу все входные переменные в прямом или инверсном виде. Такие единичные элементарные конъюнкции называют минтермами.

Таблица 2

№					Логическое выражение	Условное обозначение
0	0	0	0	0	Константа 0  “земля”
1	0	0	0	1	Конъюнкция Z = XY
2	0	0	1	0	Запрет по Y
3	0	0	1	1	Переменная X
4	0	1	0	0	Запрет по X
5	0	1	0	1	Переменная Y
6	0	1	1	0	Исключающее ИЛИ Z = XY
7	0	1	1	1	Дизъюнкция Z= XVY
8	1	0	0	0	Функция Пирса
9	1	0	0	1	Логическая равнозначность
A	1	0	1	0	Инверсия
B	1	0	1	1	Импликация
C	1	1	0	0	Инверсия
D	1	1	0	1	Импликация
E	1	1	1	0	Функция Шеффера
F	1	1	1	1	Константа 1  +Uп

Для составления переключательных функций вначале строят таблицы функционирования, или так называемые таблицы истинности. Столбцы в таблице истинности обозначают наименованиями входных и выходных переменных, а в строках записывают всевозможные сочетания входных и выходных сигналов в соответствии со словесным описанием алгоритма работы синтезируемых устройств. Покажем это на примере мажоритарного элемента, имеющего три входа X₁, X₂, X₃ и один выход Y. Единичный сигнал на выходе такого элемента должен появиться, если на двух или трех входах имеют место единичные сигналы. В противном случае на выходе должен быть нуль. Ниже представлена таблица истинности для мажоритарного элемента (табл.3).

Таблица 3

X1	X2	X3	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

На основании таблицы истинности переключательная функция может быть записана в виде

. (1)

Для построения мажоритарного элемента в соответствии с формулой (1) требуются: три инвертора для получения инверсных сигналов четыре трехвходовых элемента 3И и один четырехвходовый элемент 4ИЛИ. В большинстве случаев, применяя основные законы булевой алгебры, переключательные функции удается минимизировать, что снижает аппаратные затраты на построение устройств. Так, применяя закон дополнительности, формулу (1) можно привести к следующему более простому виду:

. (2)

Для построения того же мажоритарного элемента по формуле (2) требуются всего три двухвходовых элемента 2И и один трехвходовый элемент 3ИЛИ.

Минимизация логических функций осуществляется с целью снижения аппаратных затрат при построении комбинационных устройств. Основными критериями при минимизации являются: сокращение числа членов в переключательной функции, числа входов у используемых логических элементов, числа межсхемных соединений, а также числа логических операций, необходимых для выполнения функции. При минимизации результирующее действие переключательных функций сохраняется постоянным. Для целей минимизации переключательных функций, имеющих до трех переменных используют аналитические методы с применением основных законов алгебры логики. При большем числе переменных наиболее эффективно применение хорошо разработанного метода топологических карт Карно - Вейча, а также метода минимизации с помощью импликационных таблиц, предложенного Мак - Класки и легко реализуемого в виде машинного алгоритма.

Рассмотрим применение этих методов на примере синтеза дешифратора для управления сегментным индикатором. На рис. 1, а показан семисегментный индикатор, конструкция которого может быть реализована на основе жидких кристаллов, люминесцентных матриц, светодиодов, и т.д., а на рис. 1, б - дешифратор для управления таким индикатором. Входными сигналами является двоично-десятичный код с весо выми коэффициентами 1-2-4-8, а выходными - код, управляющий изображением десяти арабских цифр. При составлении таблицы истинности (табл. 4) условимся: если какой-либо сегмент должен быть высвечен, то такому состоянию ставим в соответствие единицу.

Таблица 4

	В х о д ы				В ы х о д ы
№	X1	X2	X3	X4	a	b	c	d	e	f	g
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1
10	1	0	1	0	*	*	*	*	*	*	*
11	1	0	1	1	*	*	*	*	*	*	*
12	1	1	0	0	*	*	*	*	*	*	*
13	1	1	0	1	*	*	*	*	*	*	*
14	1	1	1	0	*	*	*	*	*	*	*
15	1	1	1	1	*	*	*	*	*	*	*

Заполнение таблицы истинности возможно на основе состояний, приведенных на рис. 1в. На рис. 2 изображена топологическая карта Карно - Вейча для выхода а. Исходная переключательная функция при этом имеет следующий вид:

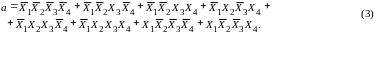
Карта - это прямоугольная матрица с числом клеток, равным 2n, где n - число переменных в переключательной функции. Каждая клетка карты имеет свой индивидуальный адрес. Правила составления и работы с картами Карно - Вейча следующие:

1. Полный адрес какой-либо клетки карты представляет собой конъюнкцию из всех входных переменных, взятых один раз в прямом или инверсном виде, и состоит из двух составляющих: адреса столбца и адреса строки. Адреса соседних столбцов или строк должны совпадать значениями на внутренних позициях и отличаться значениями на внешних. Изображают адреса в виде двоичной цифры, причем нуль соответствует инверсному значению входной переменной, а единица - прямому. Соответствие позиций адресов входным переменным отмечено в верхнем левом углу карты.

2. Карта условно считается склеенной по верхней и нижней строкам, а также по крайнему левому и правому столбцам, т.е. верхние и нижние клетки на одинаковых столбцах и крайние левые и правые клетки на одинаковых строках являются соседними.

3. В клетки карты ставят единицы, если в исходной переключательной функции присутствует конъюнкция, соответствующая данному адресу.

4. Соседние единицы карты обводят прямоугольными контурами, причем в контур должно входить число единиц, кратное степени двойки, т.е. 20, 21, 22 и т.д. (на рис. 2 намечено четыре контура).

5. Минимизированная переключательная функция равна логической сумме из содержимого всех контуров. Содержимое каждого контура равно одной конъюнкции между всеми переменными, входящими в контур только в одном каком-либо виде: прямом или инверсном.

6. Наименование переменной, для которой составляется карта, ставится в правом нижнем углу вне поля карты.

Для рассматриваемого примера минимизированная переключательная функция в соответствии с картой может быть записана в виде

. (4)

Если сравнить полученную в результате минимизации формулу (4) с исходной (3), то можно сделать следующие выводы по эффективности минимизации: 1) число логических элементов, необходимых для построения схемы, сократилось вдвое, т.е. с восьми до четырех; 2) вместо четырехвходовых элементов после минимизации требуются двух- и трехвходовые, что значительно сокращает число межэлементных соединений.

Для остальных выходов дешифратора выполняются аналогичные действия по минимизации, в результате чего можно получить следующие минимизированные переключательные функции:

Рассмотрим теперь метод Мак - Класки для минимизации исходной переключательной функции (3). Алгоритм метода ориентирован на программную реализацию с помощью ЭВМ и заключается в выполнении следующих действий:

1. В исходной переключательной функции символьные обозначения переменных заменяются на цифровые, причем на соответствующих позициях переменные только подразумеваются, а вместо них используют двоичные значения: нуль - для инверсного значения переменной и единицу - для прямого:

2. На следующем шаге цифровые конъюнкции записывают в столбец и сортируют по числу единиц. В табл. 6 первый столбец не сортированный, а второй отсортированный: нулевой столбец, столбец с одной единицей, с двумя и т.д. Для разделения друг от друга столбцы подчеркнуты.

3. Далее проводят сравнения каждого члена столбца с содержанием n единиц с каждым членом столбца с содержанием (n+1) единиц на предмет применения закона склеивания. Склеивание должно осуществляться в одной какой-либо позиции. При наличии склеивания в соответствующей позиции ставят прочерк, а против членов, для которых имели место склеивания, ставится метка (галочка).

Таблица 5

0000	0000 	00-0		00-0
0010	0010 	-000		-000
0011	1000 	001- 	0-1-	0-1-
0101	0011 	0-10 		100-
0110	0101 	100-		01-1
0111	0110 	0-11 
1000	1001 	01-1
1001	0111 	011- 

4. После первого сравнения во всех столбцах продолжают аналогичные сравнения в столбцах, получивших частичные склеивания, причем сравнивать можно только члены, имеющие прочерки на одинаковых позициях, до тех пор, пока не будут полностью исчерпаны все склеивания.

5. Если в каких-либо столбцах в результате склеивания появляются одинаковые члены, например, третья и четвертая позиции в четвертом столбце, то в силу закона повторения оставляют только один член.

В качестве результата записывают логическую сумму всех оставшихся не склеенных членов. Полученный результат представляет собой частично минимизированную переключательную функцию, так называемую тупиковую форму:

(5)

Для полной минимизации далее составляют импликационную таблицу (табл. 6), в строках которой звездочками отмечают совпадение членов, оставшихся после склеивания, с членами исходной переключательной функции. При этом для позиций, на которых имеют место прочерки, может быть любое значение в исходных членах: нуль или единица.

Таблица 6

	0000	0010	0011	0101	0110	0111	1000	1001
00-0			
-000							*
0-1-			*			
100-								
01-1						

Для импликационных таблиц имеет место следующее правило: проверяют возможность зачеркивания каких-либо строк таким образом, чтобы в столбцах, имеющих звездочки, осталась хотя бы одна. Например, этому требованию отвечает вторая строка в табл. 6. Исключая из тупиковой формы (6) член -000, получим минимизированную переключательную функцию

(6)

Переходя в формуле (6) от цифровых обозначений к символьным, видим, что минимизированная переключательная функция полностью совпадает с функцией (4). Таким образом, можно заключить, что метод Мак - Класки и метод топологических карт Карно - Вейча дают одинаковый результат минимизации.