ПлИзмЭкс_Курсовик_В23

,		1	2	12	11	22
	12.855	5.068	3.095	3.048	9.991	2.065
	0.08	0.097	0.097	0.119	0.169	0.169
	161.59	52.02	31.77	25.54	59.202	12.234

Из таблицы видно, что все коэффициенты значимы.

Осуществим поиск доверительной зоны, т.е. границ в которых будет находиться ис- тинное значение случайной величины с заданной доверительной вероятностью Р при любых значениях аргументов плана в исследуемых диапазонах.

, где

– из таблицы распределения Гауса для Р=0,95.

Подставим в последние формулы соответствующие значения , , , , выражения для и , через и приведённые выше.

Учтём, что , . После некоторых преобразований получим:

Отобразим на графике

;

;

.

Согласно заданию, теперь необходимо построить ПФЭ 2² для основных пере- менных, при этом точность определения считать одинаковой.

Спектр плана следующий:

	,	,
1
2
3
4

Требуется описать зависимость , т.е.

.

Осуществим центрирование и нормирование эксперимента, для чего введём следующие функции:

; ; ,

Теперь будем искать зависимость

Построим матрицу Адамара

1	+1	-1	-1	+1	11,850
2	+1	+1	-1	-1	15,843
3	+1	-1	+1	-1	11,830
4	+1	+1	+1	+1	28,015

Одинаковая точность определения позволяет пользоваться оценкой дисперсии средних найденной в предыдущем пункте, т.е. .

Коэффициенты , , , найдём методом наименьших квадратов:

,где ;

;; ;

16.884	5.044	3.038	3.048

Проверим полученные коэффициенты на значимость по методике описанной в пре- дыдущем пункте.

– из таблицы распределения Стьюдента для Р=0,95

	0	1	2	12
	16.884	5.044	3.038	3.048
	0.119	0.119	0.119	0.119
	141.49	42.27	25.46	25.54

Из таблицы видно, что все коэффициенты значимы.

Осуществим поиск доверительной зоны:

, где

– из таблицы распределения Гауса для Р=0,95.

Подставляя в последние формулы соответствующие значения и выражения для ,и, после некоторых преобразований получим:

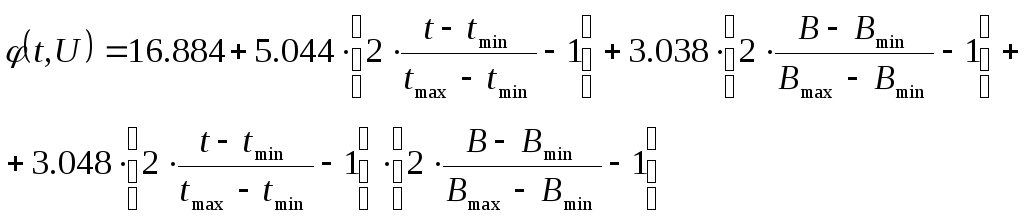
Отобразим на графике

;

;

.

В модели ПФЭ 2² в отличие от ПФЭ 3² не используются данные о средних точках плана. Значения поверхности в этих точках аппроксимируют линейными зависимос- тями проведёнными через крайние значения факторов. В силу этого значения по- верхностей в области центра плана сильно отличаются . Последнее видно из графи- ка. Проведение ПФЭ 2² экономит средства, т.к. уменьшается число экспериментов, но при этом мы можем иметь значительную погрешность в области центра плана (там где параболы должны прогибаться).

13