ПлИзмЭкс_Курсовик_В23
.docПЛАНИРОВАНИЕ ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА
Задание N 23
I. 1.Проведен эксперимент по определению зависимости Y=f(X),
результаты которого сведены в таблицу
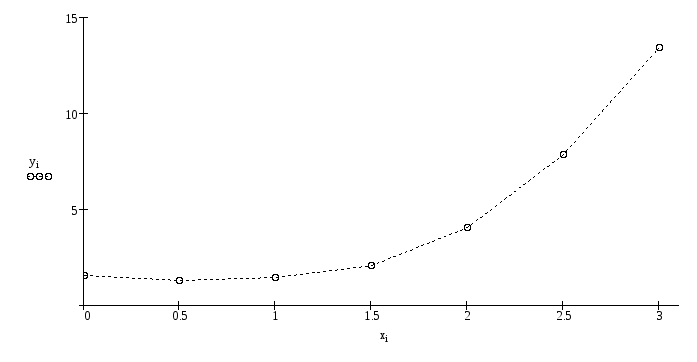
X= 0.00 0.50 1.00 1.50 2.00 2.50 3.00
Y1 2.32 2.18 1.55 2.58 4.41 7.07 13.03
Y2 1.01 0.88 1.33 1.79 4.50 7.39 13.14
Y3 1.14 1.77 0.77 2.60 3.92 7.80 13.54
Y4 1.58 1.05 2.25 1.75 3.13 8.00 13.60
Y5 1.68 0.46 1.32 1.63 4.12 8.96 13.77
2.Найти уравнение регрессии по экспериментальным данным и провести анализ
полученной модели. Доверительную вероятность принять равной Р=0,95.
II. 1.Проведен полный факторный эксперимент ПФЭ типа 32 в диапазоне факторов,
указанных в таблице и получены следующие результаты измерений
|
Ni |
t(oC) |
B(Тл) |
y1 |
y2 |
y3 |
y4 |
|
1 |
10 |
0.2 |
12.39 |
12.06 |
12.09 |
10.86 |
|
2 |
20 |
0.2 |
3.20 |
3.91 |
3.48 |
4.01 |
|
3 |
30 |
0.2 |
15.79 |
15.34 |
15.99 |
16.25 |
|
4 |
10 |
0.5 |
9.92 |
8.91 |
9.49 |
10.36 |
|
5 |
20 |
0.5 |
4.20 |
4.97 |
4.99 |
5.29 |
|
6 |
30 |
0.5 |
20.13 |
19.49 |
19.97 |
20.02 |
|
7 |
10 |
0.8 |
11.27 |
12.11 |
11.80 |
12.14 |
|
8 |
20 |
0.8 |
10.51 |
10.05 |
9.64 |
10.08 |
|
9 |
30 |
0.8 |
27.40 |
28.64 |
28.35 |
27.67 |
Определить уравнение поверхности отклика и провести анализ полученной модели. Доверительную вероятность принять равной Р=0,95
2 По результатам п.1 построить ПФЭ 22 для основных переменных . Считать точность определения Y одинаковой.
3.Дать сравнительную характеристику моделям, получаемым в п.1и 2.
-
Регрессионный анализ.
,
где
,
где
,
|
|
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
|
1,546 |
1,268 |
1,444 |
2,070 |
4,016 |
7,844 |
13,416 |
|
|
0,2141 |
0,3869 |
0,2287 |
0,1831 |
0,2389 |
0,4154 |
0,0799 |
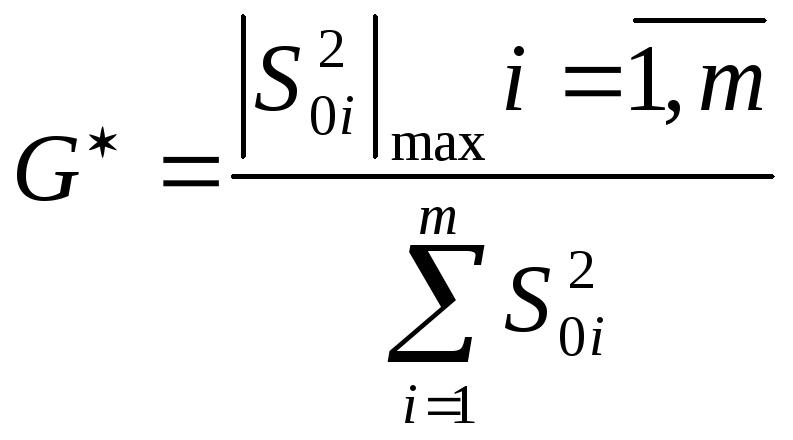
– из таблицы
распределения Кохрана для Р=0,95.
Поскольку
у нас нет оснований
отвергнуть гипотезу о равенстве дис-
персий в каждом сечении
.
–
средневзвешенная
оценка дисперсии.
–
оценка дисперсии
средних.
B качестве регрессионной модели примем:
.
Коэффициенты
найдём методом наименьших квадратов,
т.е.
.
Если функций
будут ортогональными
на счётном множестве, т.е.
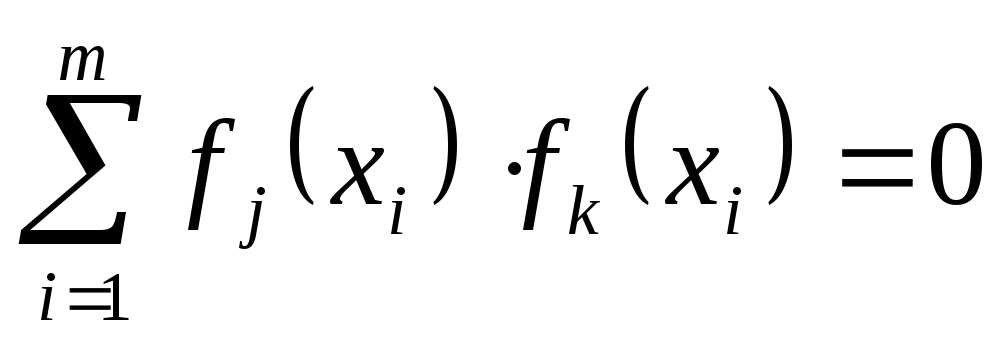при
,
то коэффициенты
находимые методом наименьших квадратов
будут определять- ся по формуле:
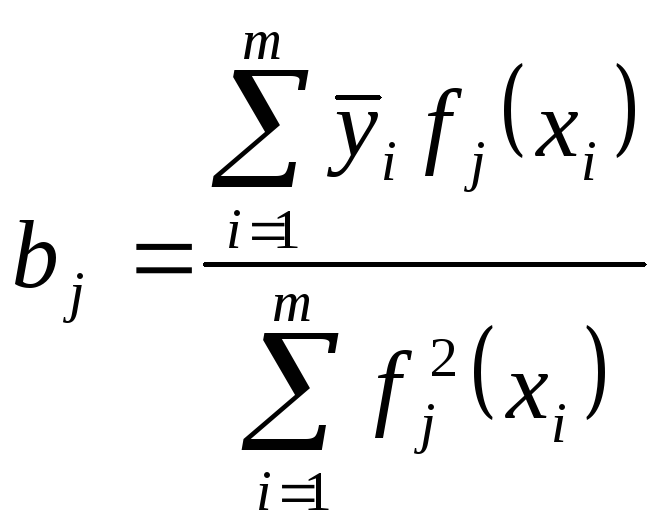
Введём безразмерную
переменную
,
где
.
Теперь будем искать
зависимость
.
Для переменной
известны
функции
удовлетворяющие условию
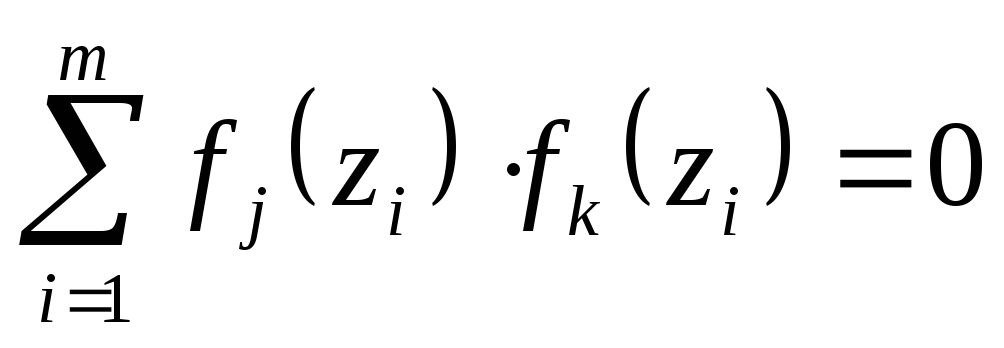при
.
Не трудно видеть,
что в данном случае функции
представляют собой полино- мы
-го порядка. Для нахождения полиномов
более высокого порядка чем первый
пользуются рекуррентным соотношением
Приступим к поиску адекватной регрессионной модели. Для адекватной модели не- обходимо выполнение условия
,
где
,
– квантили
распределения Фишера для Р=0,95.
– порядок
регрессионного полинома.
Полином нулевого порядка
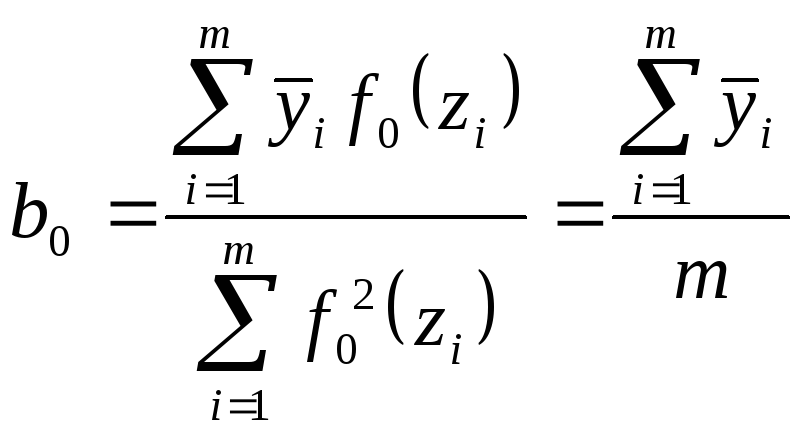
Модель не адекватна.
Полином первого порядка
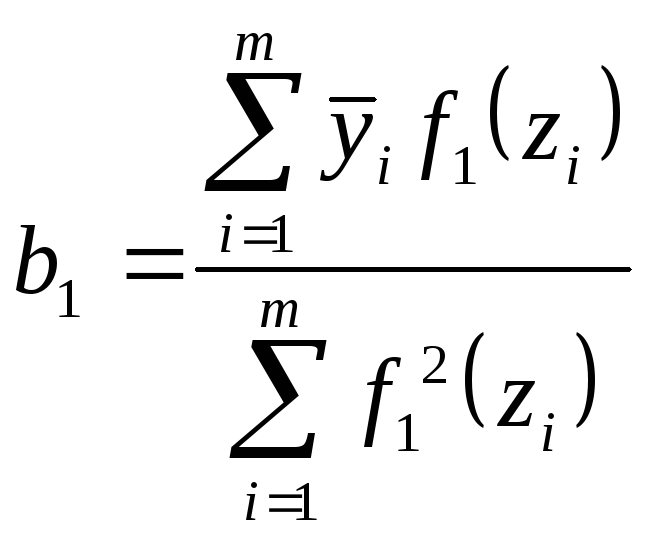
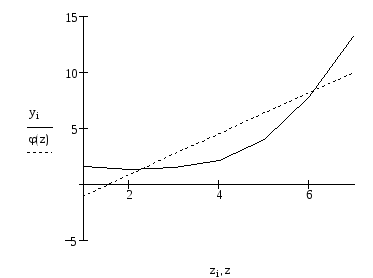
Модель не адекватна.
Полином второго порядка
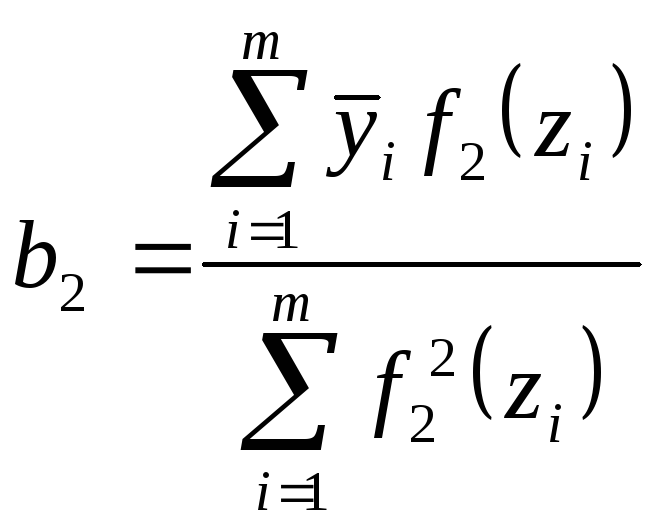
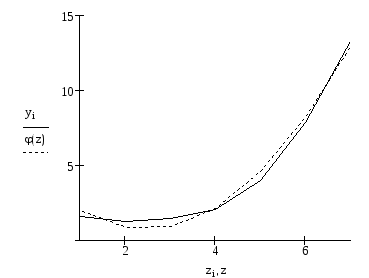
Модель не адекватна.
Полином третьего порядка
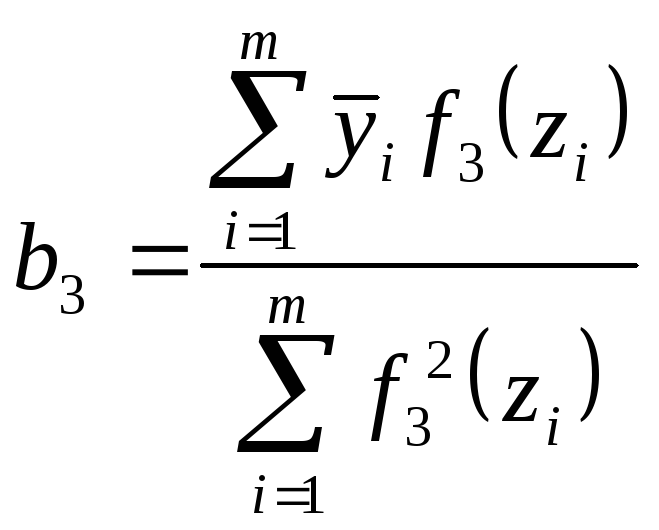
Модель адекватна.
Проверим коэффициенты
на значимость. Для того, чтобы коэффициент
был значим необходимо выполнение условия
,
где
,
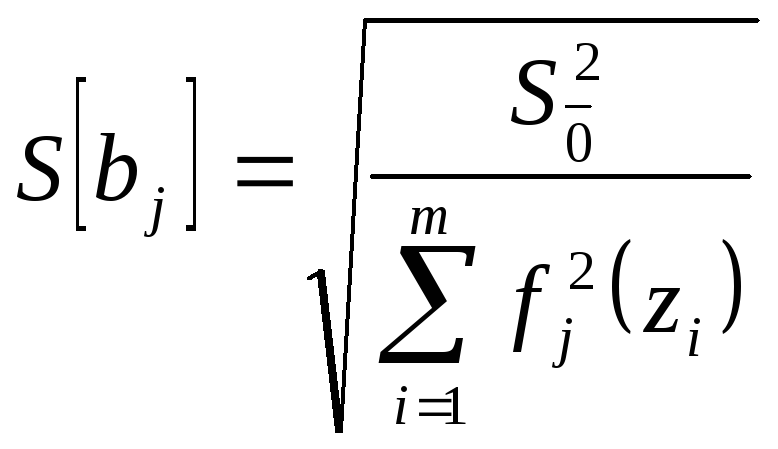– из таблицы
распределения Стьюдента для Р=0,95.
|
|
0 |
1 |
2 |
3 |
|
|
4.51 |
1.83 |
0.597 |
0.0756 |
|
|
0.084 |
0.042 |
0.024 |
0.015 |
|
|
53.47 |
43.42 |
24.49 |
4.97 |
Из таблицы видно,
что все коэффициенты
значимы.
Осуществим поиск
доверительной зоны, т.е. границ в которых
будет находиться истинное значение
случайной величины
с заданной доверительной вероятностью
Р
при любом значении аргумента регрессионной
модели в исследуемом диапазоне.
,
где
–
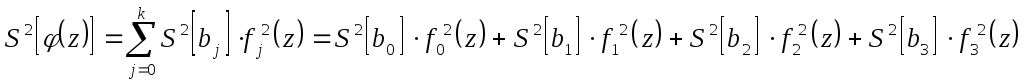
из таблицы
распределения Гауса для Р=0,95.
Подставим в
последние формулы соответствующие
значения
и выражения для
,
а также вместо
подставим выражение
для
через
приведённое выше.
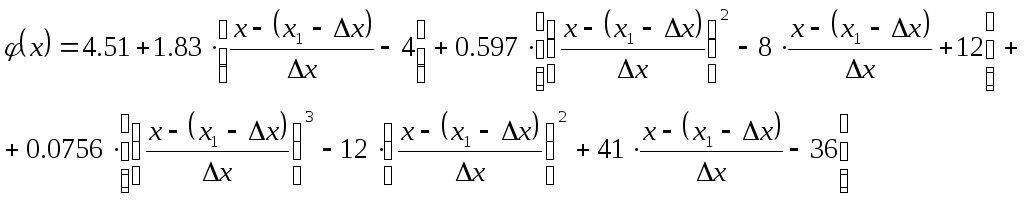
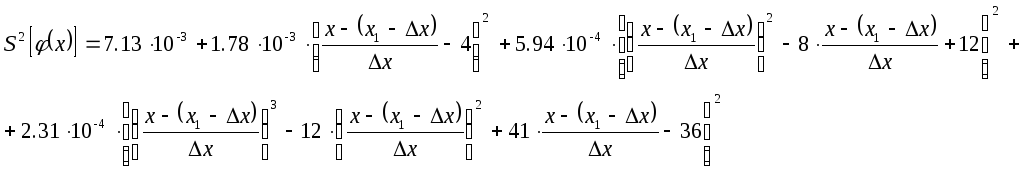
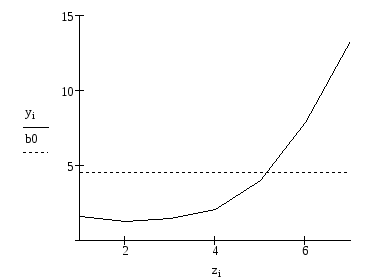
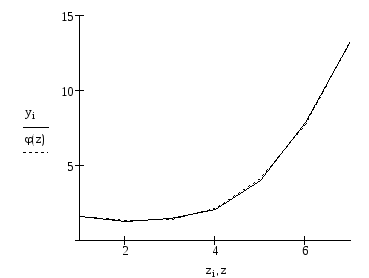
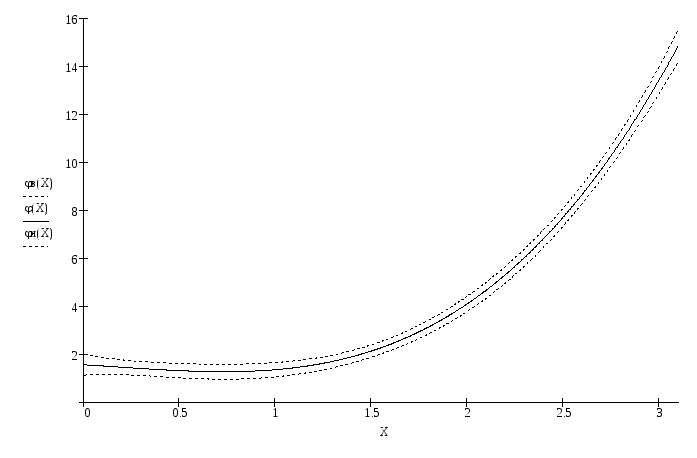
Отобразим на графике
;
;
.
-
Планирование регрессионных экспериментов.
Согласно заданию проведён ПФЭ типа 32
Требуется описать
зависимость
планом первого порядка, т.е.
.
Осуществим центрирование и нормирование эксперимента, для чего введём следующие функции:
;
;
,
где
;
;
;
Теперь будем искать
зависимость
Построим матрицу Адамара
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1/3 |
+1/3 |
11,850 |
0,458 |
|
2 |
+1 |
0 |
-1 |
0 |
0 |
+1 |
-2/3 |
+1/3 |
3,650 |
0,143 |
|
3 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1/3 |
+1/3 |
15,843 |
0,148 |
|
4 |
+1 |
-1 |
0 |
0 |
+1 |
0 |
+1/3 |
-2/3 |
9,670 |
0,383 |
|
5 |
+1 |
0 |
0 |
0 |
0 |
0 |
-2/3 |
-2/3 |
4,863 |
0,216 |
|
6 |
+1 |
+1 |
0 |
0 |
+1 |
0 |
+1/3 |
-2/3 |
19,903 |
0,080 |
|
7 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
+1/3 |
+1/3 |
11,830 |
0,163 |
|
8 |
+1 |
0 |
+1 |
0 |
0 |
+1 |
-2/3 |
+1/3 |
10,070 |
0,126 |
|
9 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1/3 |
+1/3 |
28,015 |
0,333 |
,
где
;
;
;
,
где
Последние переменные
были введены в силу того, что использование
при расчёте переменных
и
нарушает ортогональность системы.
Теперь будем искать зави- симость
,
где
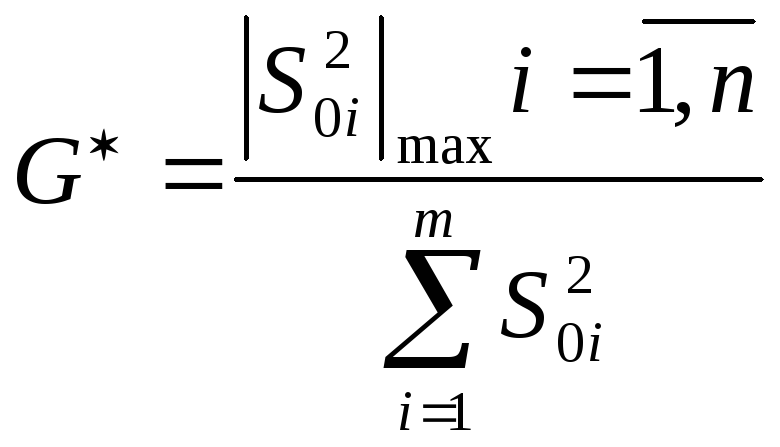
– из таблицы
распределения Кохрана для Р=0,95.
Поскольку
у нас нет оснований
отвергнуть гипотезу о равенстве дис-
персий в каждой точке
.
–
средневзвешенная
оценка дисперсии.
–
оценка дисперсии
средних.
Коэффициенты
,
,
,
,
,
найдём методом наименьших квадратов:
;
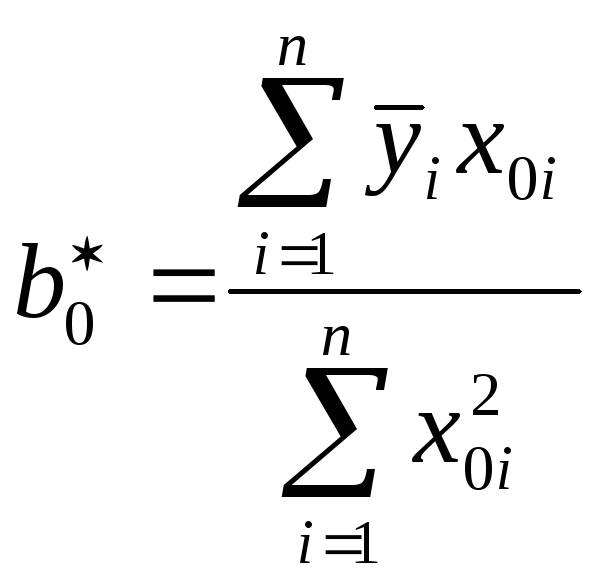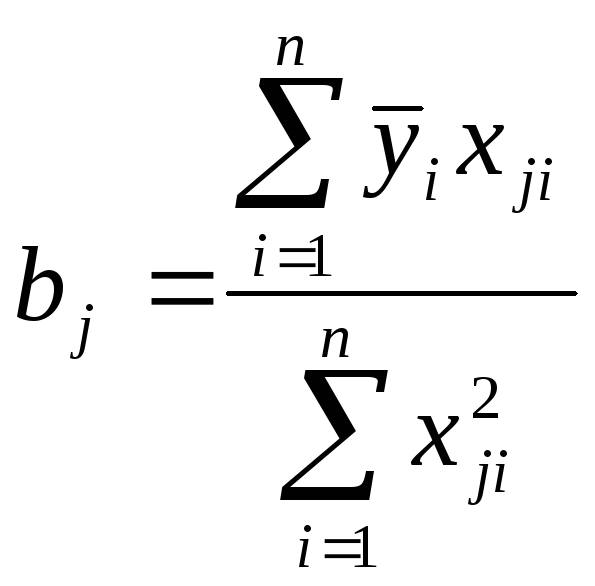,где
;
;
;
;
;
;
;
|
|
|
|
|
|
|
|
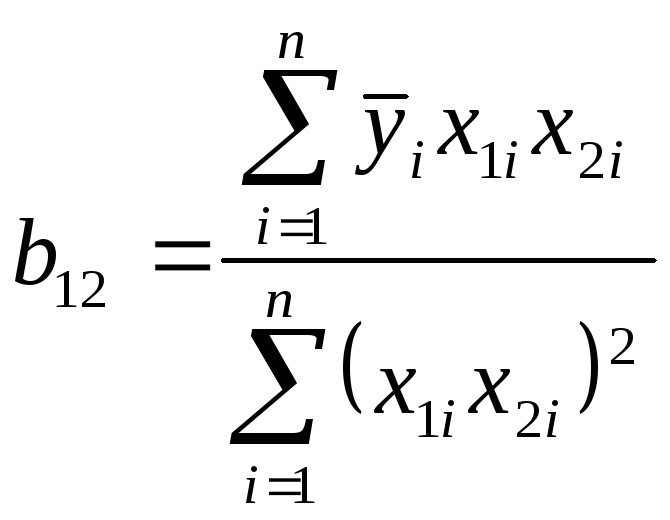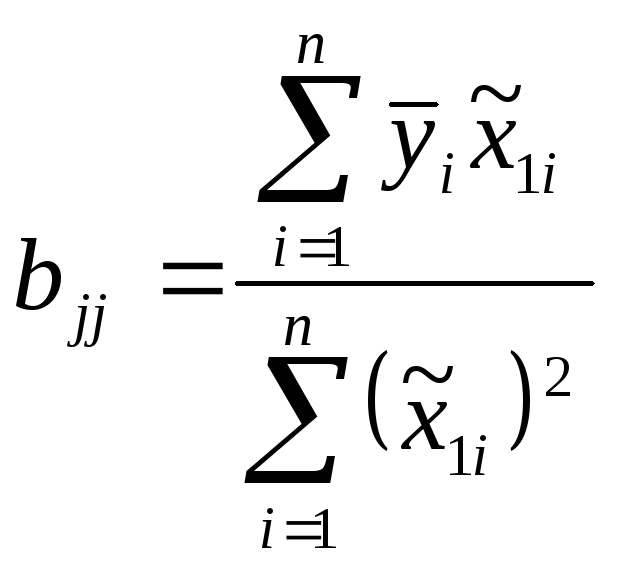
12.855 |
5.068 |
3.095 |
3.048 |
9.991 |
2.065 |
Проверим полученные
коэффициенты на значимость. Для того,
чтобы коэффициент
был значим необходимо выполнение условия
,
где
;
;
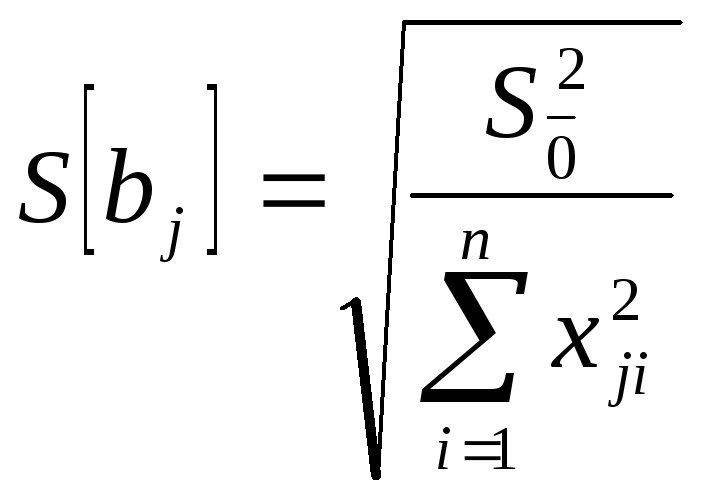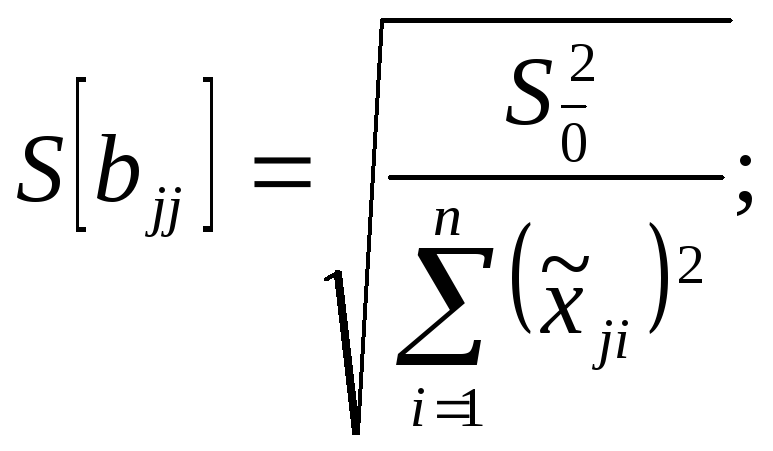
– из таблицы
распределения Стьюдента для Р=0,95.