Определим поверхность отклика при полном факторном эксперименте (пфэ)
Исходные данные можно представить следующей таблицей (2.3):
|
U, B |
t, C |
|
| |||
|
|
-20 |
20 |
| |||
|
210 |
14,93 |
14,8 |
| |||
|
230 |
14,93 |
15,53 |
| |||
|
14,93 |
14,8 |
14,93 |
15,53 | |||
Необходимо найти зависимость вида F(x1,x2)=b0+b1x1+b2x2+b12x1x2 , где b0, b1, b12 – коэффициенты; а x1 и x2 – параметры (в нашем случае параметром x1 будем считать t, а параметром x2 – U).
9. Осуществим центрирование исходных диапазонов значений параметров, используя формулу:
Исходя из приведённой формулы, получаем значение коэффициента:
Аналогично находим x20: x20=220.
10. Осуществим нормирование исходного диапазона. Для этого воспользуемся формулой:
11. Теперь перейдём к центрированной и нормированной системе координат:
и
получим:
Аналогичные действия проводим с остальными значениями параметров, в результате чего получаем таблицу 2.4:
|
z2k |
z1k |
|
|
-1 |
1 | |
|
-1 |
14,93 |
14,8 |
|
1 |
14,93 |
15,53 |
12. Составляем таблицу (2.5) базисных функций:
|
Ni |
z0 |
z1 |
z2 |
z1z2 |
yср |
|
1 |
1 |
-1 |
-1 |
1 |
14,93 |
|
2 |
1 |
1 |
-1 |
-1 |
14,8 |
|
3 |
1 |
-1 |
1 |
-1 |
14,93 |
|
4 |
1 |
1 |
1 |
1 |
15,53 |
13. Определим коэффициенты bj:
Для этого воспользуемся формулой:
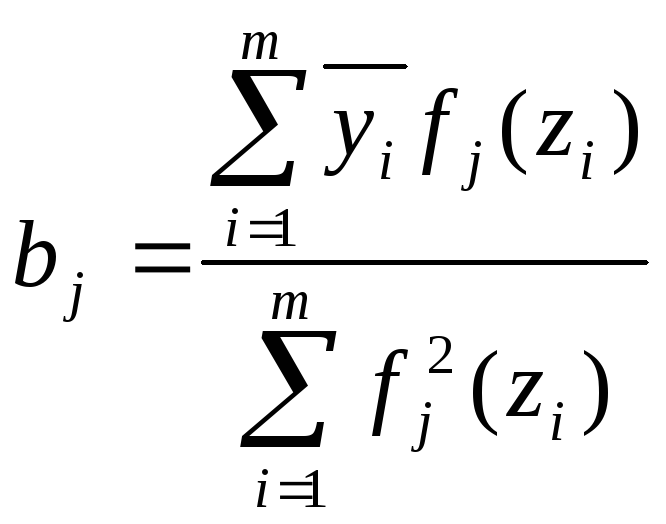
Отсюда
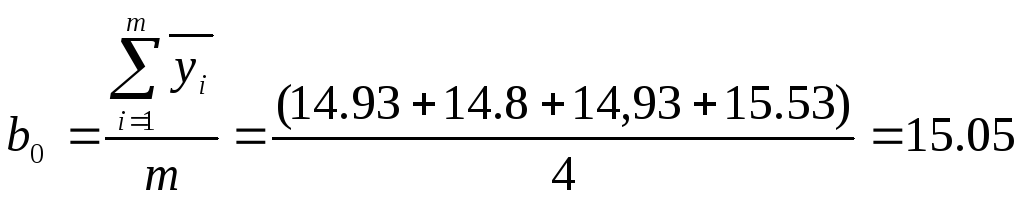
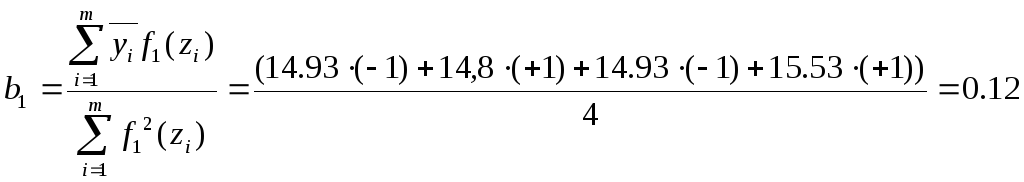
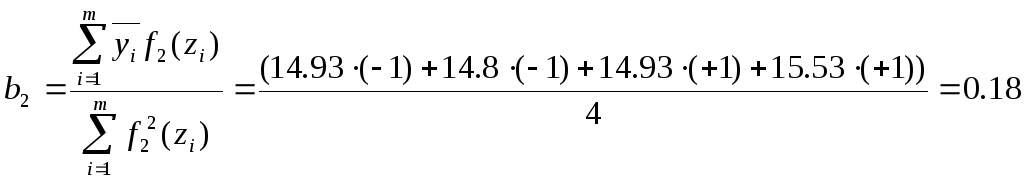
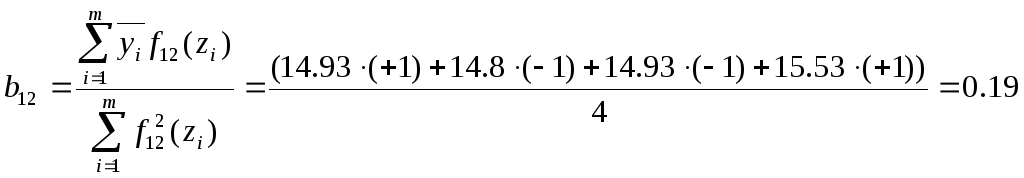
В результате получаем функцию: F(z1,z2)=15,05+0,12z1+0,18z2+0,19z1z2
Плоскость, построенная по данному уравнению, совпадает с плоскостью, построенной по экспериментальным данным.
Проверим значимость коэффициентов b0, b1, b2, b12
14. Найдём соответствующие оценки дисперсий коэффициентов b0, b1, b2, b12. Общая формула имеет следующий вид:
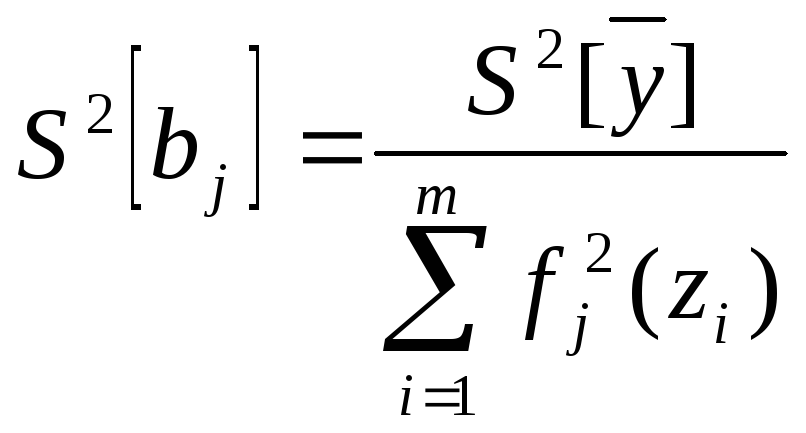
В результате получаем:
15. Проверим значимость коэффициентов b0, b1, b2 по критерию Стьюдента. Найдём отношения:
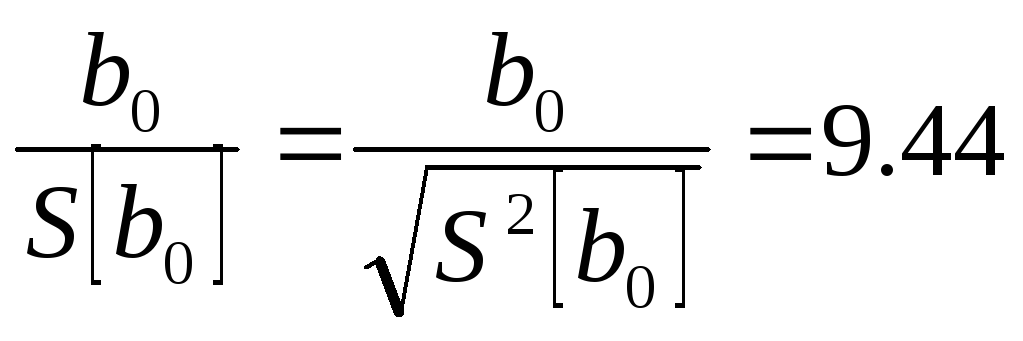
tP(mn-m) = t0.95(12) = 0.079. Так как полученные значения больше коэффициента Стьюдента tP(mn-m), то коэффициенты являются значимыми.
16. Найдём суммарную дисперсию полученных коэффициентов:
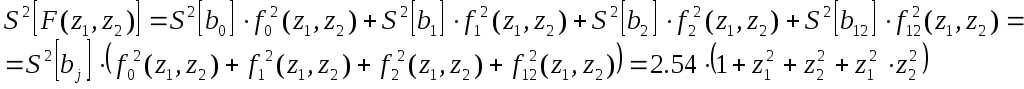
Переходим от ортогональных базисных функций к исходной метрике.
17.
Перейдём к пространству x.
Для этого воспользуемся формулой:
Отсюда
получаем:
Подставим значения в исходную функцию для z:
В результате упрощения получаем:
F(x1, x2) = 11.06 – 0.19x1 + 0.02x2 + 0,00093x1x2
18. Найдём суммарную дисперсию коэффициентов для пространства x:
Для этого подставим в формулу для суммарной дисперсии вместо z1, z2 соответствующее выражение:
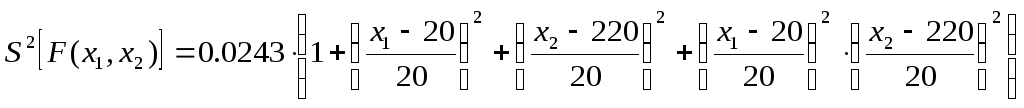
В результате упрощения получаем следующее выражение:
Напишем уравнение для граничных значений: Fгр(x1,x2)=Fист(x1,x2)±2*S[F(x1,x2)]
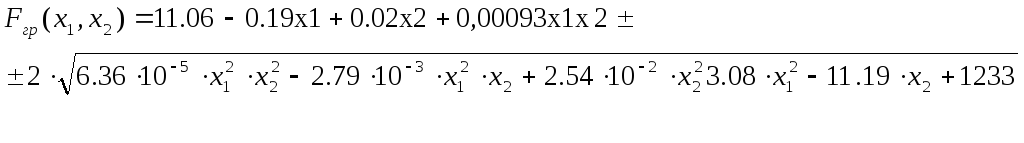
Приведём таблицы для нижней, исходной и верхней плоскостей:
Нижняя пл-ть(2.6) Получ. пл-ть(2.7) Верхняя пл-ть(2.8)
|
U, B |
t, C |
|
|
U, B |
t, C |
|
|
U, B |
t, C |
|
|
|
-20 |
20 |
|
-20 |
20 |
|
-20 |
20 | ||
|
210 |
8,6 |
8,4 |
210 |
14,9 |
14,8 |
210 |
21,3 |
21,2 | ||
|
230 |
8,5 |
9,2 |
230 |
14,9 |
15,5 |
230 |
21,3 |
21,9 |
Построим соответствующий полученной зависимости однофакторный (классический) эксперимент
19. Из полученной зависимости F(z1,z2)= 15,05+0,12z1+0,18z2+0,19z1z2 найдём 4 (2N=4, где N – число факторов) точки, необходимые для построения однофакторного (классического) эксперимента. Это точки с координатами (в z-пространстве) (-1;0); (1;0); (0;-1); (0;1). Сведём получившиеся результаты в таблицу 2.9 (необходимые точки выделены жирным шрифтом):
|
z2k |
z1k |
|
|
|
|
-1 |
0 |
1 |
|
-1 |
14,93 |
14,87 |
14,79 |
|
0 |
14,93 |
15,05 |
15,16 |
|
1 |
14,93 |
15,23 |
15,53 |
20. Составляем таблицу (2.10) базисных функций:
|
Ni |
z0 |
z1 |
z2 |
z1z2 |
yср |
|
1 |
1 |
-1 |
0 |
0 |
14,93 |
|
2 |
1 |
1 |
0 |
0 |
15,16 |
|
3 |
1 |
0 |
-1 |
0 |
14,87 |
|
4 |
1 |
0 |
1 |
0 |
15,23 |
21. Определим коэффициенты bj:
Для этого воспользуемся формулой:
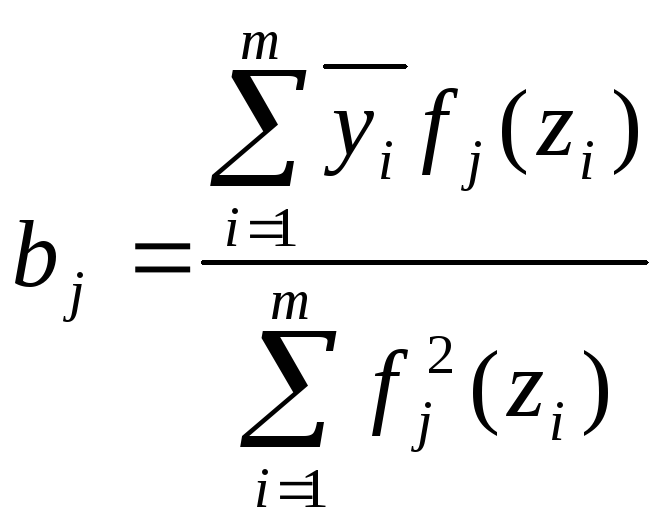
Отсюда
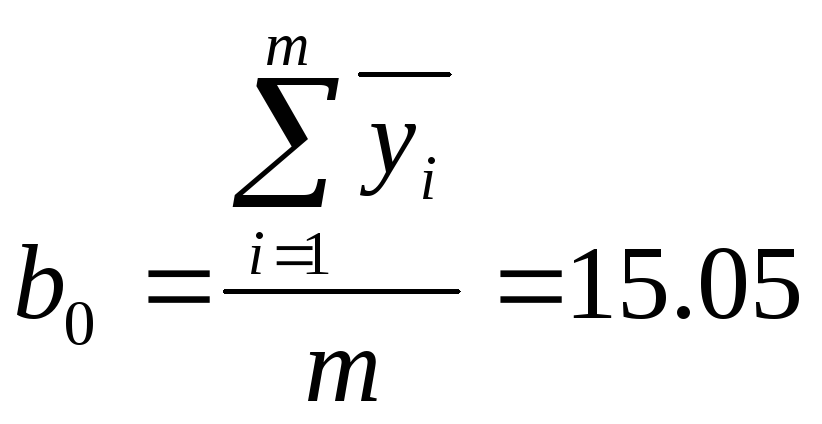
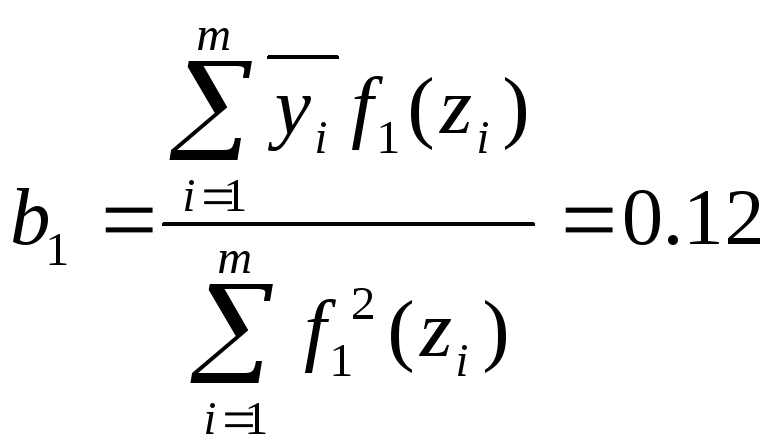
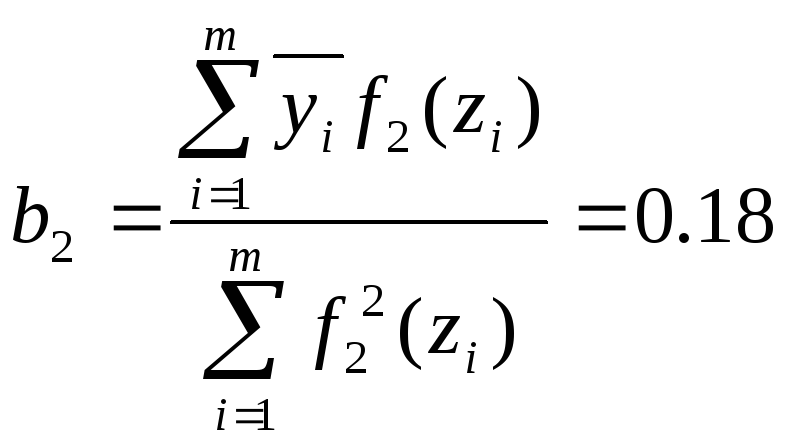
В результате получаем функцию: F(z1,z2)= 15,05+0,12z1+0,18z2
Плоскость, построенная по данному уравнению, имеет следующие значения (таблица 2.11).
|
z2k |
z1k |
|
|
|
|
-1 |
0 |
1 |
|
-1 |
12,72 |
7,63 |
12,71 |
|
0 |
7,63 |
2,54 |
7,62 |
|
1 |
12,72 |
7,62 |
12,71 |