2.1. Случайные функции и их характеристики

Геологические модели исследуемого геологического пространства создаются на основе анализа комплексной геологической информации. Среди этой информации важное место занимают геологические, геохимические и геофизические поля, полученные в результате геологических, геохимических и геофизических съемок различного уровня, каротажа скважин и др.

Определение 1.1

Случайной называют функцию, которая в результате испытания принимает тот или иной конкретный вид, заранее неизвестно какой именно.

Случайные функции - это упорядоченные по времени или пространству случайные величины. Примерами случайных функций в геологической практике, как уже отмечалось, являются: результаты опробования вдоль горных выработок, измерения геофизических или геохимических полей, измерения вариаций магнитного поля в течение дня, данные каротажа скважин и документации скважин и др.

Определение 1.2

Случайная функция, аргументом которой является время, называется случайным процессом F(t).

Определение 1.3

Случайная функция, аргументом которой является координаты пространства, называется случайным полем F(x).

Каждый конкретный вид, который принимает случайная функция в результате испытания, называется ее реализацией.

При проведении серии испытаний получают семейство реализаций случайной функции.

Р ис7.1

Примером такого семейства являются контрольные измерения геофизического поля по одному и тому же профилю.

Определение 1.4

Совокупность значений случайной функции для любого фиксированного значения аргумента xj называется сечением случайной функции и является обычной случайной величиной F(xj).

Для этой случайной величины можно вычислить математическое ожидание M[F(x_j)], дисперсию D[F(x_j)] и другие характеристики, построить функцию плотности распределения f_Fj и т.д. Если вычислить математическое ожидание и дисперсию для каждого значения аргумента х случайной функции, получим математическое ожидание M[F] и дисперсию D[F] случайной функции.

Математическое ожидание случайной функции характеризует некоторую среднюю функцию, вокруг которой колеблются все ее реализации.

(7.1)

Дисперсия случайной функции характеризует разброс реализаций относительно математического ожидания случайной функции.

(7.2)

Здесь: F_k(x_i) - реализация случайной функции

K - количество реализаций.

Определение 1.5

Случайная функция называется стационарной, если ее математическое ожидание, дисперсия и автокорреляционная функция не изменяются с изменением аргумента.

Определение 1.6

Стационарные функции, характеристики которых полученные по одной реализации, являются представительными для всех реализаций и для всей функции в целом, называются эргодическими.

Р ис. 7.2

На рис. 7.2. приведены стационарные случайные функции, кроме того F₁ и F₃ являются также и эргодическими.

Для эргодических случайных функций оценки статистических характеристик могут вычисляться по более простым формулам по одной реализации.

(7.3)

(7.4)

где: n- число значений случайной функции в одной реализации.

Математическое ожидание определяет среднюю линию, а дисперсия - полосу, в которой осуществляются реализации случайной функции. Однако, поведение функции внутри полосы бывает совершенно различным.

Так, например, F₁ и F₂ имеют примерно одинаковые M[F] и D[F], однако, колебания функций различны.

Определение 1.7

Характеристикой изменчивости какой-либо реализации функции вдоль оси абсцисс может служить величина зависимости между соседними значениями функции. Эта зависимость оценивается автокорреляционной функцией (АКФ).

Для функций с дискретным аргументом (т.е. когда измерения проведены по регулярной сети). Автокорреляционная функция вычисляется по формуле:

AKФ_F(θ) = r_F( (7.5)

Где (7.6)

Автоковариационная функция:

здесь: - величина сдвига реализации случайной функции, равная 1,2,..m пикетам.

Рассмотрим пример вычисления автокорреляционной функции.

П усть дана реализация случайной функции. Рис.7.3(a).

Рис. 7.3(а)

Вычислим математическое ожидание M[F] и вычтем его из значений функции в результате получим:

xi	1	2	3	4	5	6	7	8	9	10
Fxi-М[F]	4	-4	6,5	10	3,7	-8,5	2,1	2,5	-2,0	-4,8

Требуется построить автокорреляционную функцию.

1. Пусть =0

xi	1	2	3	4	5	6	7	8	9	10
Fxi-М[F]	4	-4	6,5	10	3,7	-8,5	2,1	2,5	-2,0	-4,8
Fxi-М[F]	4	-4	6,5	10	3,7	-8,5	2,1	2,5	-2,0	-4,8

K_F(0)=

K_F(0) = 30,2; r_F(0) =1

Значение автоковариационной функции для =0 соответствует

д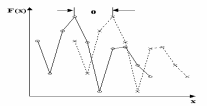 исперсии D[F]=30,2.

Рис. 7.3(б)

2. Пусть =1 K_F1(1)=

xi		1	2	3	4	5	6	7	8	9
Fxi-М[F]		4	-4	6,5	10	3,7	8,5	2,1	2,5	-2,0
Fxi+1-М[F]	4	-4	6,5	10	3,7	8,5	2,1	2,5	-2,0	-4,8

K_F1(1)=

K_F(1)=6,6 r_F(1)=0,219

3. Пусть =2 K_F2(2)=

x1			1	2	3	4	5	6	7	8	9
Fxi-М[F]			4	-4	6,5	10	3,7	8,5	2,1	2,5	-2.0
Fxi+2-М[F]	4	-4	6,5	10	3,7	-8,5	2,1	2,5	-2,0	-4,8

K_F(2)=-8,6 r_F(2)= -0,285

4. Сдвигая функцию в дальнейшем на =3,4,5,...m (Рис. 10.3(б)) получим последующие значения функций.

K_F(3)=-1,8 r_F(3)=-0,06

K_F(4)=10,0 r_F(4)=0,33

K_F(5)=-1,2 r_F(5)=0,04

Н а рисунке 7.3(в) приведен график автокорреляционной функции для нашего примера.

Рис. 7.3(в)

Автокорреляционная функция симметрична относительно вертикальной оси. При =0, r_F(0)=1.

Для различных автокорреляционная функция представляет собой коэффициенты корреляции двух случайных величин F(x_i) и F( ).

Числовой характеристикой зависимости значений случайной функции вдоль профиля является радиус корреляции R, т.е. такое среднее расстояние, на котором сохраняется положительная корреляционная связь в структуре случайной функции.

В простейшем случае радиус корреляции (R) представляет собой расстояние от начала координат до пересечения r_F с осью абсцисс. Удвоенный радиус корреляции 2R характеризует средний полупериод колебаний случайной функции. Если R<1 - исследуемая функция называется некоррелируемой.