Теорема 2.4.

Всякий многочлен Р(z) степени n  2 на множестве комплексных чисел разлагается на п линейных множителей:

Р(z) = а_п(z – ₁)(z – ₂)...(z – _п),

где а_п – старший коэффициент, а _k , k = 1, 2, ..., n, – корни многочлена Р(z).

Доказательство: Пусть Р(z) = а_пz^п + а_п–1z^п–1 + ... + а₁z + а₀ . Согласно основной теореме алгебры, многочлен Р(z) имеет корень, обозначим его ₁. Тогда справедливо разложение на множители

Р(z) = (z – ₁)Р_п-1(z).

Но по той же теореме многочлен Р_п-1(z) имеет корень ₂, значит

Р_п-1(z) = (z – ₂)Р_п-2(z),

откуда Р(z) = (z – ₁) (z – ₂)Р_п-2(z), и т. д.

После п–го шага получим

Р(z) = (z – ₁)(z – ₂)...(z – _п)Р₀,

где Р₀ –многочлен нулевой степени. Сравнивая в этом равенстве старшие коэффициенты слева и справа, получаем а_п = Р₀, откуда и следует равенство

Р(z) = а_п(z – ₁)(z – ₂)...(z – _п).

Причем, числа ₁, ₂, ₃, …, _п – корни многочлена Р(z), поскольку из полученного равенства легко найти Р(_i) = 0, i= 1,2,…, n. Теорема доказана..

Если среди корней _k есть кратные, то разложение примет вид

где т₁, т₂, ... , т_r – кратности корней ₁, ₂, ... , _r соответственно, причем т₁+ т₂ + ... + т_r = п.

Следствие 1.

Всякий многочлен на множестве комплексных чисел имеет ровно п корней, причем каждый корень считается столько раз, какова его кратность.

Итак, на множестве комплексных чисел любой многочлен разложим на линейные множители, а, следовательно, всегда приводим. Среди многочленов с действительными коэффициентами неприводимыми являются только линейные многочлены вида z –  и квадратные многочлены z² + рz + q, не имеющие действительных корней.

Следствие 2.(теорема Виета)

Пусть ₁, ₂, …, _n – корни многочлена Р(z) = z^п + а_п–1z^п–1 + ... + а₁z + а₀ , старший коэффициент которого равен 1. Тогда коэффициенты этого многочлена связаны с его корнями ₁, ₂, …, _n соотношениями:

а₀ = (–1)^п ₁^.₂^.… ^._n,

а₁ = (–1)^п(₁^.₂^.… ^._n–-1 + ₁^.₂^.… ^._n–-2^._n + … + ₂^.₃^.… ^._n),

…………………………………………………………………….,

а_п–2 = ₁₂ + ₁₃ + … + _п–1_п,

а_п–1 = – (₁ + ₂ + … + _п)

Теорема 2.5.

Если многочлен с действительными коэффициентами имеет комплексный корень  + i , то сопряженное число  – i также является корнем этого многочлена.

Доказательство теоремы предлагаем провести самостоятельно для многочлена второй степени .

Это означает, что если многочлен с действительными коэффициентами имеет комплексный корень, то в его разложении на неприводимые множители с действительными коэффициентами обязательно будет множитель второй степени z² + рz +q, дискриминант которого D= p² –4q< 0.

Из теоремы 2.4 и теоремы 2.5 следует

Теорема 2.6.

Всякий многочлен с действительными коэффициентами представим в виде произведения линейных и квадратичных множителей, т.е.

Р(z) = а_п(z ­– ₁)(z ­– ₂)…(z ­– _s)(z² + p₁ z+ q₁)(z² + p₂ z+ q₂)…(z² + p_t z+ q_t), (3)

где ₁, ₂, …, _s – действительные корни многочлена Р(z), а квадратные трехчлены (z² + p_k z+ q_k), k = 1, 2, …, t, имеют отрицательные дискриминанты.

Равенство (3) называют разложением многочлена на неприводимые множители. Заметим, что если среди корней многочлена есть кратные, то разложение примет вид

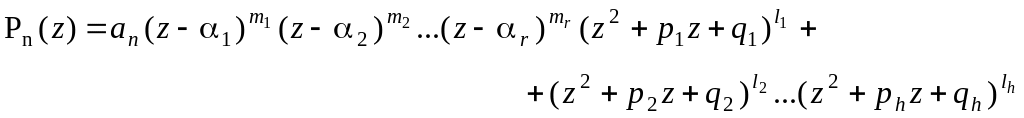, (4)

где .

Рассмотрим теоремы, позволяющие в некоторых частных случаях найти корни многочлена.