2.5. Лабораторная работа
Расчет температурных полей и средней температуры в межвалковом зазоре (симметричный процесс)
Цель лабораторных работ.
Ознакомление с методикой расчета температурных полей и средней температуры в межвалковом зазоре для симметричного процесса переработки на валковых машинах.
Программное обеспечение:
1. MS-DOS QBasic Copyright <C> Microsoft Corporation.
2. Программы расчета температурных полей в валковых машинах.
Последовательность выполнения работы.
1. Изучение теоретической части практикума.
2. Получение исходных данных у преподавателя.
3. Открытие и запуск программ на ЭВМ, ввод исходных данных и получение расчетных значений.
4. Составление отчета.
5. Ответ на контрольные вопросы.
Получаемые результаты.
Параметры температурных полей для симметричного процесса переработки на валковых машинах.
Содержание отчета.
Титульный лист, теоретическая часть (очень краткое изложение представленного материала), практическая часть (исходные данные, рассчитанные значения), выводы.
Температурное поле в межвалковом зазоре при симметричном процессе каландрования (вальцевания) определяется на основании решения уравнения энергии (2.32)
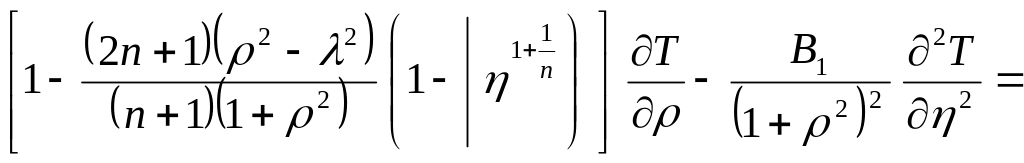
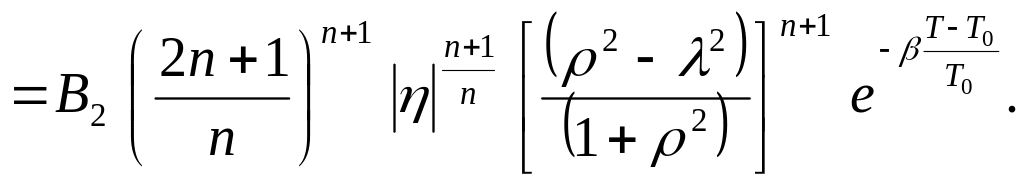(2.32)
Краевые условия для решения уравнения (2.32) следующие:
Уравнение энергии относится к параболическому типу, одним из самых распространенных методов решения таких уравнений является метод конечных разностей. Сравнивая коэффициенты при производных уравнения энергии (2.32) и уравнения (2.33)
(2.33)
можно установить, что
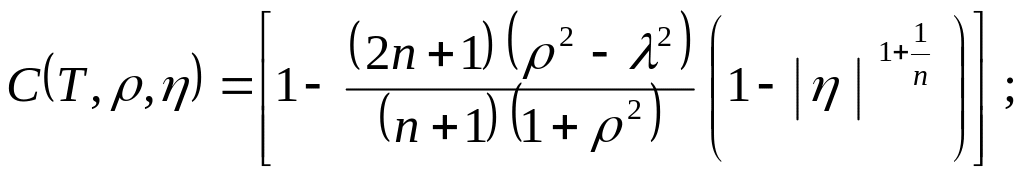(2.34)
(2.35)
(2.36)
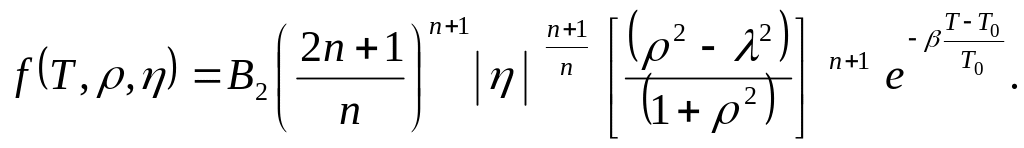(2.37)
Если коэффициенты граничных условий (2.38), (2.39)
(2.38)
(2.39)
принять равными
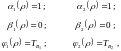(2.40-2.42)
то эти граничные условия преобразуются к виду граничных условий уравнения (2.32).
Границы изменения переменной - Н. Для переменной границы изменения: а = -1, b = +1.
Структурная схема алгоритма расчета температурных полей и средней температуры в межвалковом зазоре представлена на рис. 2.5, а идентификаторы к программе № 5 – табл. 2.1.
Блок 1. Вводятся исходные данные: реологические свойства перерабатываемого полимера – коэффициент консистентности k0, температурный коэффициент , температура Т0 и показатель степени реологического уравнения n; размеры межвалкового зазора – минимальная ширина 2Н0, координаты Н и , радиус валков R, окружная скорость валков UB, температура валков ТB1, и ТB2, начальное распределение температур ТН. Границы изменения переменной . Координата первого слоя конечно – разностной сетки = Н.
Блок 2. Задается число шагов на слое n и рассчитывается число узлов на слое n1 = n + 1.
Блок 3. Задаются описания коэффициентов граничных условий (2.40) – (2.42).
Блок 4. Вводятся описания коэффициентов дифференциального уравнения (2.32) (см. формулы (2.34 – 2.36)).
Блок 5. Вводятся описания функций, выражающих зависимости коэффициента теплопроводности Н(Т), удельной теплоемкости сп (Т) и плотности п (Т) от температуры для данного полимерного материала.
Блок 6. Задаются описания постоянных В1 и В2 уравнения энергии (2.42)
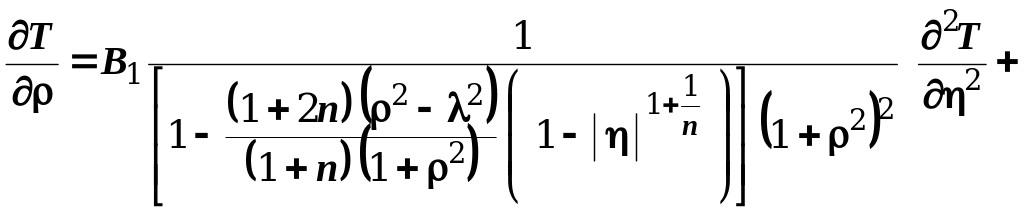
(2.43)
Блок 7. Задаются шагом по переменной - , числом распечатки массива температур по слоям с1 рассчитывается шаг по переменной - . Переменной присваивается значение нижней границы изменения.
Блок 8. Начинается цикл расчета температур в узлах первого слоя.
Блок 9. Рассчитывается распределение температур в узлах первого слоя Т’i согласно начальному условию. Эти значения присваиваются элементам вспомогательного массива Si, рассчитывается координата i узлов на слое.
Блок 10. Рассчитывается координата следующего слоя конечно – разностной сетки.
Блок 11. Предварительно задаются значением температуры в первом узле конечно – разностной сетки.
Блок 12. Рассчитываются значения теплофизических свойств полимера в первом узле конечно – разностной сетки.
Блок 13. Рассчитываются значения постоянных В1 и В2 уравнения энергии (2.43) в первом узле.
Блок 14. Переменной присваивается значение нижней границы.
Блок 15. Рассчитывается значение коэффициентов 1, 1, 1, 2, 2, 2 граничных условий в первом узле.
Блок 16. Рассчитывается значение коэффициентов дифференциального уравнения в первом узле.
Блок 17. Рассчитывается прогоночные коэффициенты Р1 и Q1 по уравнению
(2.44,2.45)
Блок 18. Открывается цикл расчета прогоночных коэффициентов Рi, Qi во внутренних узлах сетки.
Блок 19. Рассчитываются коэффициенты А и F дифференциального уравнения.
Блок 20. Рассчитывается координата узла конечно – разностной сетки.
Блок 21. Предварительно задаются значением температуры во внутренних узлах сетки.
Блок 22. Рассчитываются коэффициенты В1 и В2 дифференциального уравнения энергии (2.43).
Блок 23. По предварительно заданному значению температуры рассчитываются значения теплофизических свойств перерабатываемого полимера во внутренних узлах конечно – разностной сетки.
Блок 24. Рассчитываются коэффициенты К и С дифференциального уравнения (2.32).
Блок 25. По уравнениям
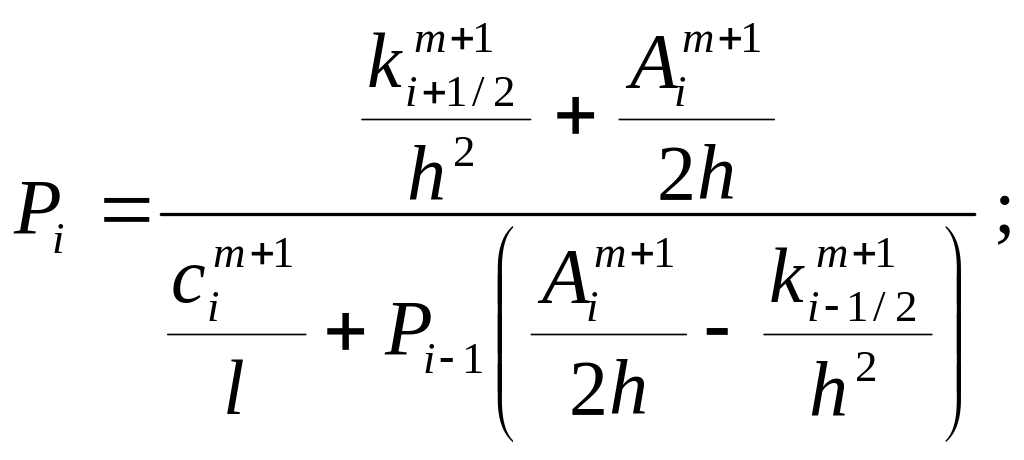(2.46)
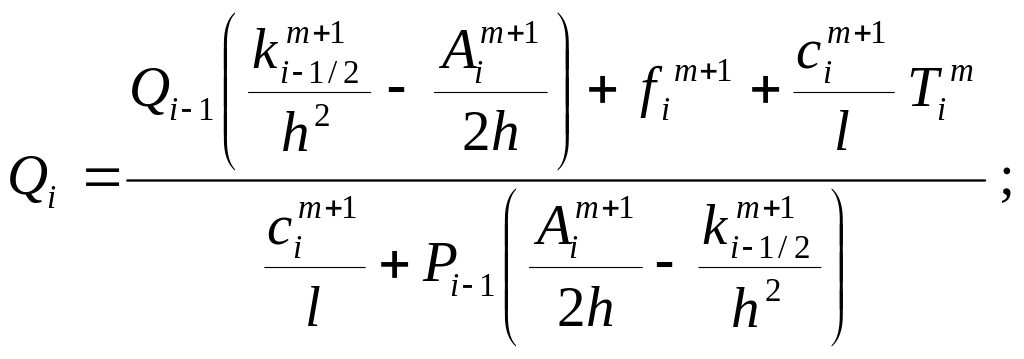(2.47)
определяются коэффициенты прогонки Рi и Qi во внутренних узлах конечно - разностной сетки.
Блок 26. Предварительно задаются температурой в последнем узле конечно - разностной сетки.
Блок 27. По предварительно заданной температуре рассчитываются теплофизические свойства перерабатываемого полимера
Блок 28. Определяются постоянные В1 и В2 уравнения энергии (2.43).
Блок 29. Рассчитывается значение координаты последнего узла конечно – разностной сетки.
Блок 30. Определяются коэффициенты 2, 2, 2 граничных условий.
Блок 31. Рассчитываются коэффициенты С, k, А, f дифференциального уравнения (2.32).
Блоки 32-33. Рассчитываются прогоночные коэффициенты и значение температуры в последнем узле конечно – разностной сетки по уравнениям
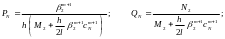(2.48)
Блок 34. Рассчитывается разность между заданным для определения теплофизических свойств и полученным значением температуры в последнем узле.
Блок 35. Открывается цикл обратной прогонки.
Блок 36. По уравнениям
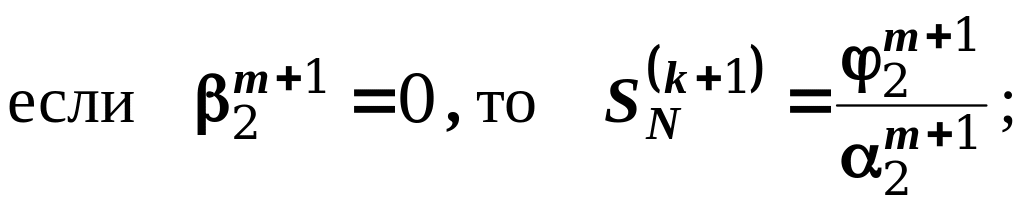(2.49)
(2.50)
(2.51)
рассчитывается первое приближение температуры.
Блок 37. Рассчитывается разность между заданным значением температур для расчета теплофизических свойств полимера и значениями температур, полученными в первом приближении.
Блоки 38 - 39. Определяется максимальная разность температур.
Блок 40. Вспомогательному массиву температур S [N 1] присваивается значение, полученные в первом приближении.
Блок 41. Рассчитывается допускаемая погрешность.
Блок 42. Максимальная разность температур сравнивается с допускаемой погрешностью. Если максимальная разность температур превышает допускаемую погрешность, то расчет повторяется, начиная с блока 11.
Блоки 43- 44. Искомому массиву температур присваивается значение вспомогательного массива. Рассчитывается сумма значений температур на слое.
Блоки 45 - 48. На заданном слое выводится на печать массив температур.
Блок 49. Координата слоя сравнивается с координатой выхода полимера из межвалкового зазора.
Блок 50. Рассчитывается средняя температура по межвалковому зазору по формуле
(2.52)
Блок 51. Распечатывается значения температур на выходе из межвалкового зазора и средней температуры по зазору.
Программа расчета температурных полей и средней температуры в межвалковом зазоре при симметричном процессе каландрования представлена ниже.
10 PRINT "Температура поля в зазоре"
20 PRINT "симметричный процнсс"
21 INPUT "Введите температурный коэффициент b=", BE
22 INPUT " Введите температуру То=", T0
23 INPUT " Введите зазор Но=", H0
24 INPUT " Введите радиус валков Rb=", Rb
25 INPUT " Введите окружную скорость Ub=", CK
26 INPUT " Введите температуру валков Tb1=", T1
27 INPUT " Введите температуру валков Tb2=", T2
30 DATA 1, -1, 1.2, 1.2, -.4
40 READ JA, JU, TH, T, SH
41 LPRINT " Введите температурный коэффициент b="; BE
42 LPRINT " Введите температуру То="; T0
43 LPRINT " Введите зазор Но ="; H0
44 LPRINT " Введите радиус валков Rb = "; Rb
45 LPRINT " Введите окружную скорость Ub="; CK
46 LPRINT " Введите температуру валков Tb1="; T1
47 LPRINT " Введите температуру валков Tb2="; T2
50 DATA .245, 1.3E+05, 1.5
60 READ NR, KR, FR
70 N = 10: N1 = N + 1
80 DIM U(N1), S(N1), P(N1), Q(N1), M(N1)
90 DEF FND (Z) = 1: DEF FNE (Z) = 0
100 DEF FNG (Z) = 1: DEF FNH (Z) = 0
110 DEF FNJ (Z) = T1: DEF FNL (Z) = T2
120 DEF FNC (II, Z, W) = 1 - ((1 + 2 * NR) * (W ^ 2 - SH ^ 2) * (1 - ABS(Z) ^ (1 + 1 / NR))) / ((1 + NR) * (1 + W ^ 2))
130 DEF FNK (II, Z, W) = AK / (1 + W ^ 2) ^ 2
140 DEF FNF (II, Z, W) = BK * EXP(-BE * (II - T0) / (T0 + 273)) * ((1 + 2 * NR) / NR) ^ (1 + NR) * ABS(Z) ^ (1 + 1 / NR) * ABS((W ^ 2 - SH ^ 2) / (1 + W ^ 2) ^ 2) ^ (1 + NR)
150 DEF FNA (II, Z, W) = 0
155 DEF FNF1 (J) = .195
160 DEF FNF2 (J) = -.024404 + .0029034 * J - 1.23617E-05 * J ^ 2
170 DEF FNF3 (J) = .0745588 + 7.8622E-04 * J - 5.88253E-08 * J ^ 2
180 DEF FNF4 (J) = 852.794 + .4525351 * J - 5.43782E-03 * J ^ 2
190 DEF FNF5 (J) = 740.3829 + 1.05226 * J - 5.88235E-03 * J ^ 2
200 DEF FNC1 (J) = 1811.78 - .64626 * J + .0392 * J ^ 2
210 DEF FNC2 (J) = 6041.64 - 39.6986 * J - .307912 * J ^ 2 + 3.20726E-03 * J ^ 3
220 DEF FNC3 (J) = -102272! + 657.037 * J
230 DEF FNC4 (J) = -4344.871 + 38.8332 * J
240 DEF FNAK (J) = LA * SQR(2 * Rb * H0) / (RO * CP * H0 ^ 2 * CK)
250 DEF FNBK (J) = (1 / (2 ^ NR)) * KR * SQR(Rb / 2) * CK ^ NR / (RO * CP * H0 ^ (NR + .5))
260 TS = 0: C1 = 1: V = .1: Y = (JA - JU) / N: X = JU: B1 = 1 / Y: G1 = B1 ^ 2: D1 = 1 / V:
CY = 0
270 FOR I = 1 TO N1
280 M(I) = 150: U(I) = M(I): S(I) = U(I): X = X + Y
290 NEXT I
300 T = T - V: R = 0
310 TP = S(1): GOSUB 740
315 AK = FNAK(T): BK = FNBK(T)
320 X = JU: GE = FNJ(T): EL = FND(T): I1 = FNE(T)
330 IF I1 = 0 THEN 340 ELSE 350
340 P(1) = 0: Q(1) = GE / EL: GOTO 390
350 FI = 0: CH = FNK((S(1) + S(2)) / 2, X + Y / 2, T): PE = FNK(S(1), X, T):
IJ = FNA(S(1), X, T)
360 CE = EL * (PE - Y * IJ / 2) - I1 * CH * B1: EE = -I1 * Y * FNC(S(1), X, T) * D1 / 2
370 CE = 1 / (CE + EE): IJ = GE * (PE - Y * IJ / 2) - I1 * Y * FNF(S(1), X, T) / 2 + EE * U(1)
380 P(1) = -I1 * CH * B1 * CE: Q(1) = IJ * CE
390 FOR I = 2 TO N
400 I1 = FNC(S(I), X, T) * D1: EE = FNA(S(I), X, T) / 2
410 X = X + Y: TP = S(I): GOSUB 740
415 AK = FNAK(T): BK = FNBK(T)
420 CE = FNK((S(I) + S(I - 1)) / 2, X - Y / 2, T): IJ = FNK((S(I) + S(I + 1)) / 2, X + Y / 2, T)
430 GE = -G1 * CE + B1 * EE: EL = -G1 * IJ - B1 * EE
440 PE = FNF(S(I), X, T) + I1 * U(I): I1 = I1 + G1 * (CE + IJ): CE = -1 / (I1 + GE * P(I - 1))
450 P(I) = EL * CE: Q(I) = (GE * Q(I - 1) - PE) * CE
460 NEXT I
470 TP = S(N1): GOSUB 740
475 AK = FNAK(T): BK = FNBK(T)
480 X = X + Y: GE = FNL(T): EL = FNG(T): I1 = FNH(T)
490 IF I1 = 0 THEN 500 ELSE 510
500 IJ = GE / EL: FI = ABS(IJ - S(N1)): S(N1) = IJ: GOTO 550
510 PE = FNK(S(N1), X, T): IJ = FNA(S(N1), X, T): CH = FNK((S(N) + S(N1)) / 2, X - Y / 2, T): CE = I1 * CH * B1 + EL * (PE + Y * IJ / 2)
520 EE = I1 * Y * FNC(S(N1), X, T) / 2 * D1: IJ = I1 * Y * FNF(S(N1), X, T) / 2 + GE * (PE + Y * IJ / 2) + EE * U(N1): CE = 1 / (CE + EE)
530 P(N1) = I1 * CH * B1 * CE: Q(N1) = IJ * CE: IJ = (Q(N) * P(N1) + Q(N1)) / (1 - P(N) * P(N1))
540 FI = ABS(IJ - S(N1)): S(N1) = IJ
550 FOR I = N TO 1 STEP -1
560 IJ = P(I) * S(I + 1) + Q(I): B = ABS(S(I) - IJ)
570 IF B > FI THEN FI = B
580 S(I) = IJ
590 NEXT I
600 EE = Y ^ 4: R = R + 1: IF R > 0 THEN 620
610 IF FI > EE THEN 320
620 FOR I = 1 TO N1
630 U(I) = S(I): TS = TS + U(I)
640 NEXT I
650 CY = CY + 1
660 IF CY = C1 THEN 670 ELSE 700
670 CY = 0: PRINT : PRINT "T="; T
680 PRINT "’Температура:"
690 FOR I = 1 TO N1: PRINT U(I), : NEXT I
700 IF T > SH THEN 300
710 TC = TS / (N1 * (INT((TH - SH) / V) + 1)): PRINT : PRINT "T="; T
720 FOR I = 1 TO N1: PRINT U(I), : NEXT I
730 PRINT : PRINT "TC="; TC: GOTO 810
740 IF TP >= 171 THEN 750 ELSE 760
750 CP = FNC4(TP): RO = FNF5(TP): LA = FNF3(TP): GOTO 800
760 CP = FNC1(TP): RO = FNF4(TP): LA = FNF1(TP)
770 IF TP >= 102 THEN CP = FNC2(TP) ELSE 790
780 IF TP >= 164 THEN CP = FNC3(TP) ELSE 790
790 IF TP >= 120 THEN LA = FNF2(TP) ELSE 800
800 RETURN
810 END
Контрольные вопросы.
1. Что такое «температурные поля»?
2. Что такое «средняя температура» применительно для процесса?
3. Как рассчитываются температурные поля?
4. Описание математической модели применяемой в работе.
5. Обоснование использования qBasic для программирования математических моделей.
6. Достоинства и недостатки qBasic. Современные версии Basic.
7. Основные допущения математической модели.
8. Обоснование полученных результатов. Вводы по работе.