III. Колебательное движение

Колебаниями называют любой физический процесс, повторяющийся через равные промежутки времени.

Механические колебания – это колебания, при которых тело, выведенное из положения равновесия, регулярно возвращается обратно, в положение равновесия.

1. Гармонические колебания

Гармонические колебания это такие колебания, при которых в зависимости от времени, колебательный процесс идет по закону синуса или косинуса.

Рассмотрим гармонические колебания на примере движения материальной точки по окружности. Пусть точка М движется по окружности радиуса OM = R = A, где A – амплитуда, φ – угол поворота. ON = x – смещение. При движении точки M по окружности, величина x изменяется, колеблется от + до – .

Э то колебательный процесс, который идет по закону синуса:

, соответственно , где - угловая скорость, циклическая частота.

Если есть начальное колебание с углом поворота то

2. Основные характеристики гармонического колебания

1) - смещение, отклонение точки от положения равновесия в каждый момент времени (измеряется в метрах).

2) - амплитуда, это максимальное смещение (в метрах).

3) - период, т.е. время одного полного колебания.

4) - циклическая частота (Гц).

5) - частота, это число колебаний в секунду (Гц).

- фаза колебаний, - начальная фаза.

Фаза измеряется в радианах, иногда в градусах. Фаза показывает, какая часть периода прошла от начала колебаний. Фаза взаимосвязана с периодом колебаний в соответствии с графиком гармонических колебаний:

3. Скорость и ускорение при гармонических колебаниях

Скорость гармонических колебаний при :

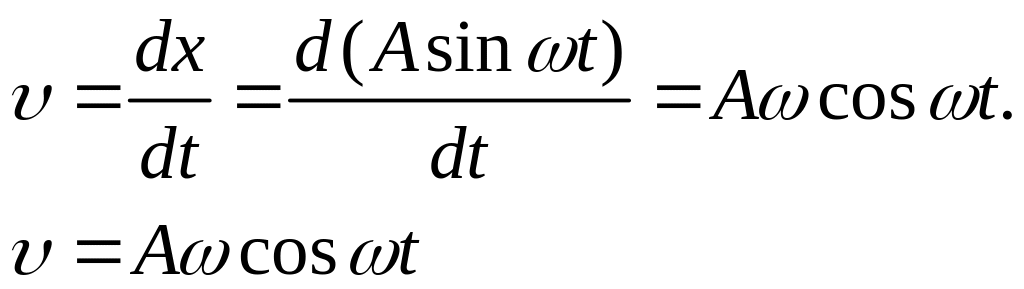
Ускорение гармонических колебаний – первая производная от скорости по времени:

или:

4. Энергия гармонических колебаний

1. Кинетическая энергия.

Так как ,

то:

,

где .

2. Потенциальная энергия колебания

упруго деформированного тела

Так как ,

то: ,

где - потенциальная энергия упруго деформированного тела.

- коэффициент жесткости (или упругости), определяется из уравнения:

Получено, что:

По закону сохранения энергии:

(так как ).

Сумма кинетической и потенциальной энергии в любой момент движения равна его максимальной кинетической или максимальной потенциальной энергии.

6. Пружинный маятник

Пусть материальная точка подвешена на пружине

p=mg- вес тела, F_упр - сила упругости.

Если тело оттянуть вниз, то на материальную точку будет действовать упругая сила больше, чем величинаmg:

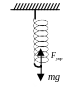
^{и поэтому возникают колебания, при которых:}

F_упр= -kx (по закону Гука)

Т.к. .

Из этих уравнений следует:

,

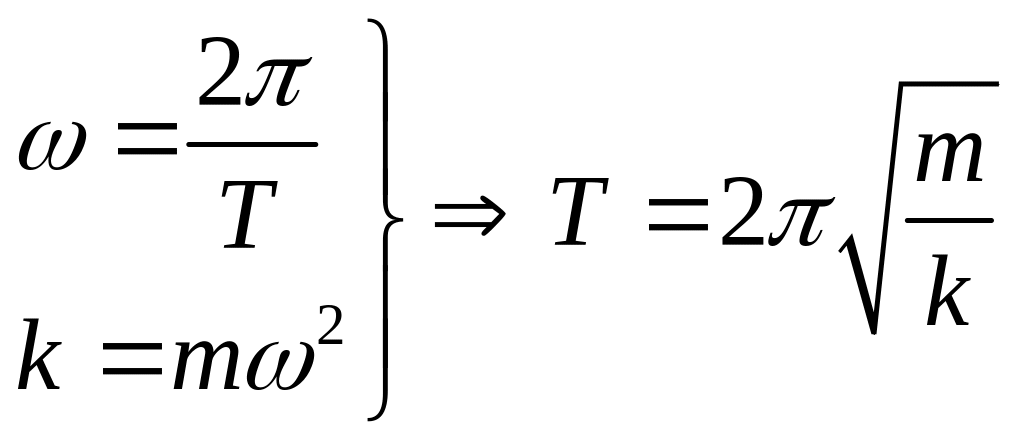где - период колебаний пружинного маятника.

7. Математический маятник

Математический маятник – это материальная точка, подвешенная на невесомой и нерастяжимой нити. По закону Гука:

Из формул:

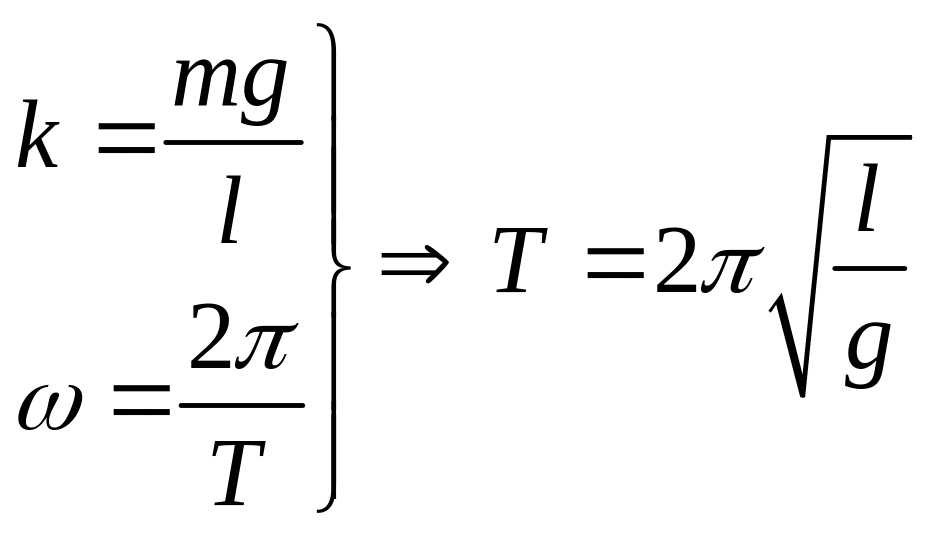
Здесь:_T- период; _l- длина маятника; _g- ускорение свободного падения; _mg- сила тяжести.