
- •Министерство образования Российской Федерации Саратовский государственный технический университет
- •Непрерывных систем
- •А. Реакция на ступенчатый стимул
- •D. Эквивалентная электрическая схема (на пассивных элементах)
- •G. Диаграмма полюсов (*) и нулей (0) в комплексной частотной области ()
- •3. Рекомендации по решению задачи
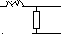
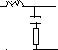
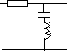
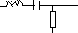
D. Эквивалентная электрическая схема (на пассивных элементах)
Стимул
![]() -
идеальный источник напряжения, реакция
-
идеальный источник напряжения, реакция![]() - снимаемое напряжение.
- снимаемое напряжение.
В вариантах 1-6: R=1 C=1 L=1
2.
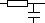
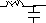
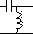



3.
(E
) (![]() )
)
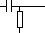

 4.
5.
6.
4.
5.
6.
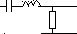
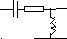
В вариантах 7-12: R=2 C=0.5 L=1
 7.
8.
9.
7.
8.
9.
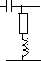 10.
11.
12.
10.
11.
12.
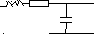
В вариантах 13-18: R=3 L=1 C=0.5
13. 14. 15.
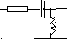
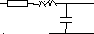
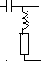 16.
17.
18.
16.
17.
18.
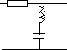

E. Динамическое уравнение системы
В скобках указаны начальные условия при ступенчатом
воздействии:
![]() .
.
F. Системная функция H(p)=Y(P)/X(P)
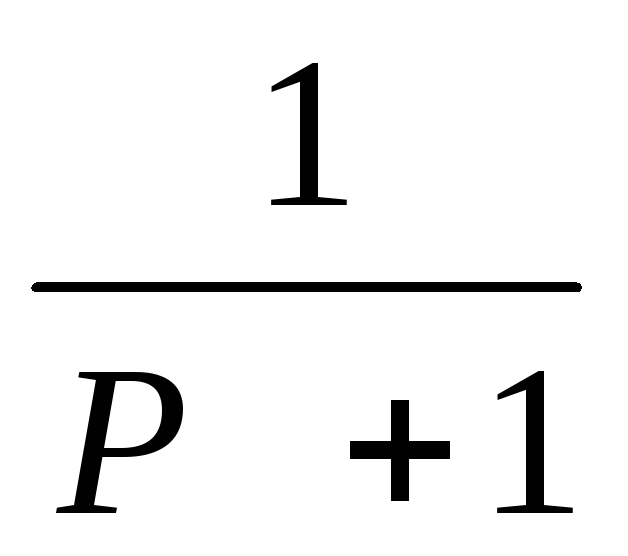 9.
9.
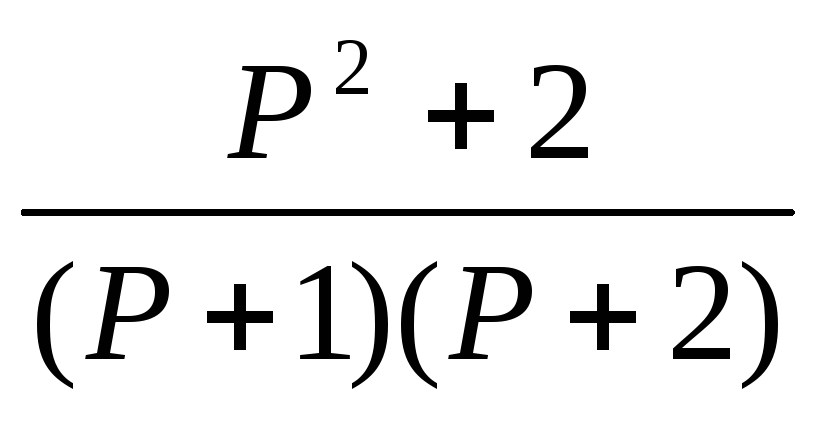
2.
![]() 10.
10.![]()
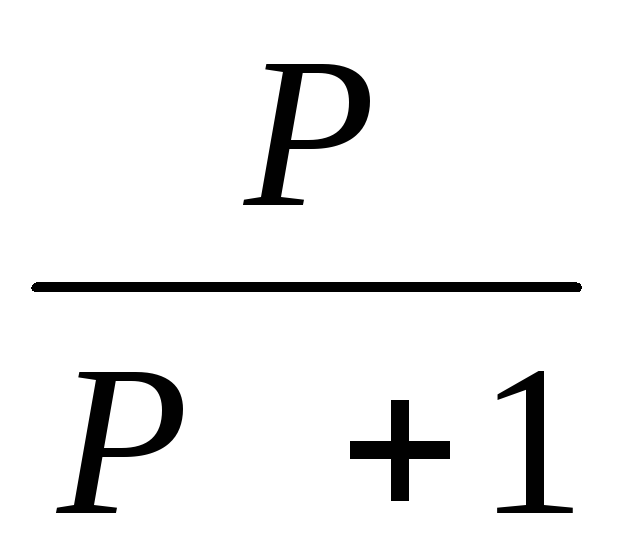 11.
11.
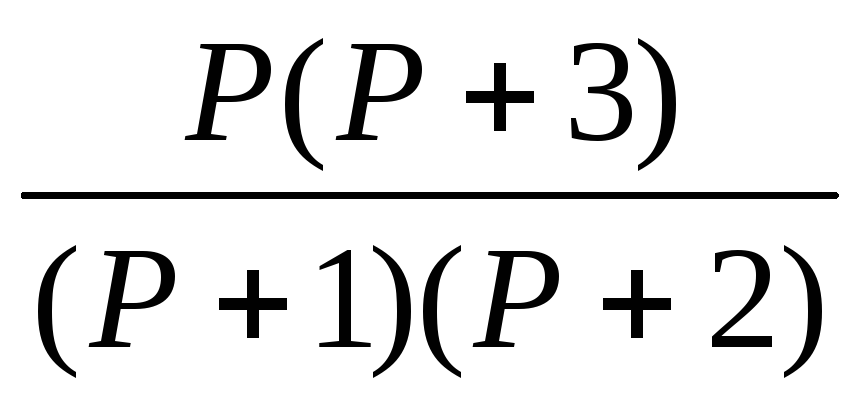
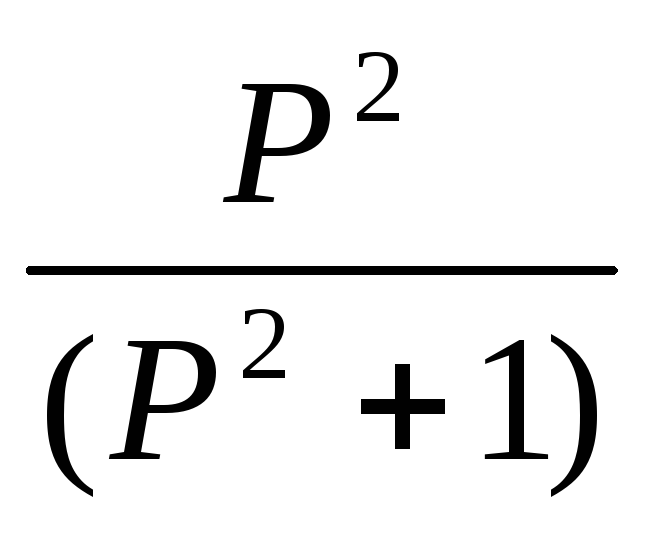 12.
12.
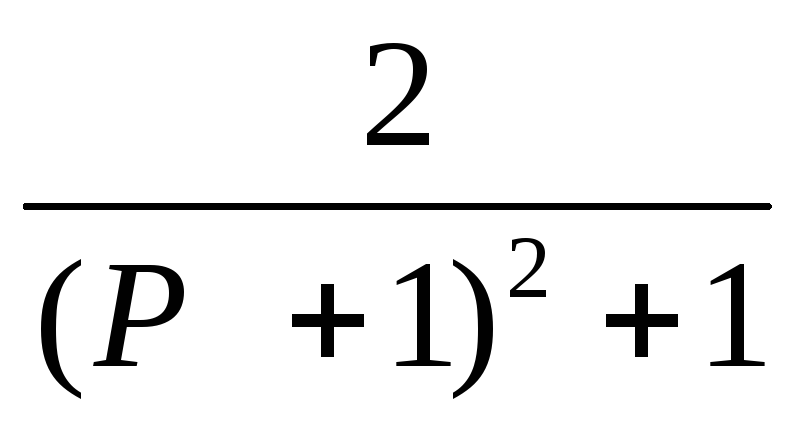
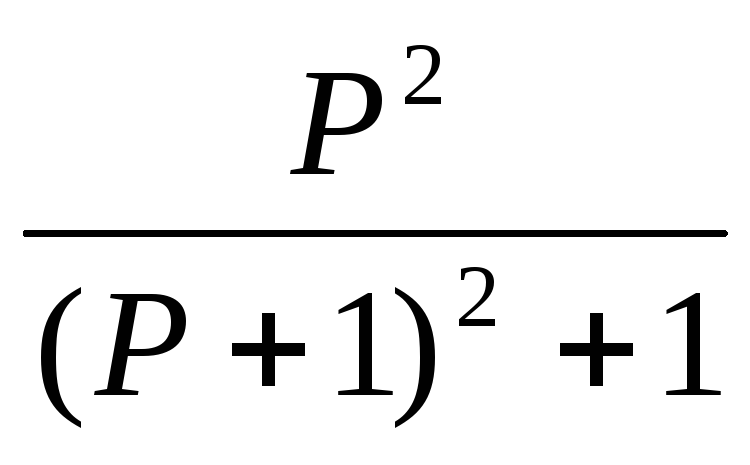 13.
13.
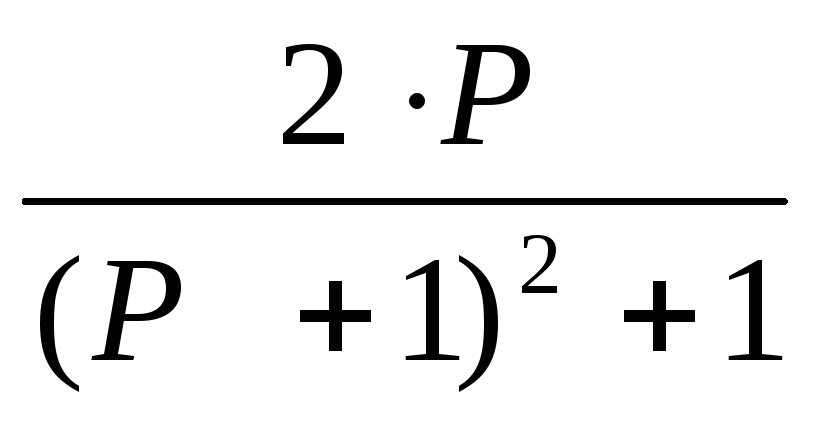
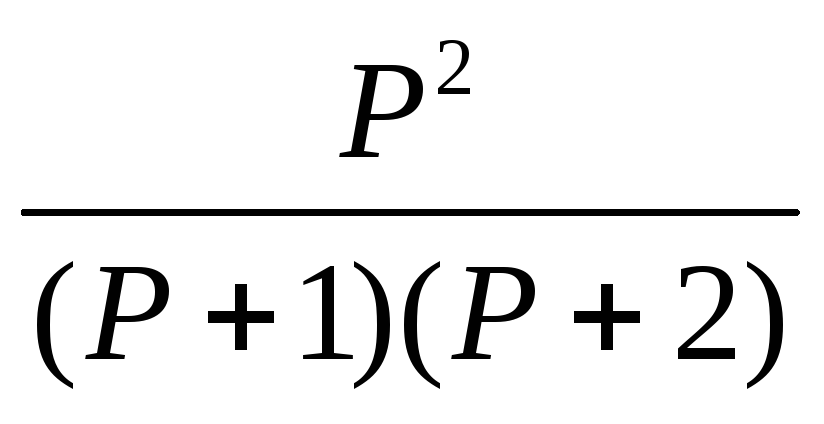 14.
14.
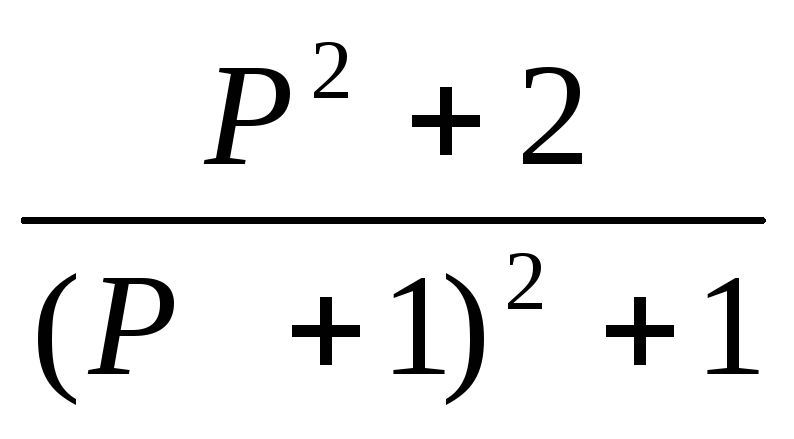
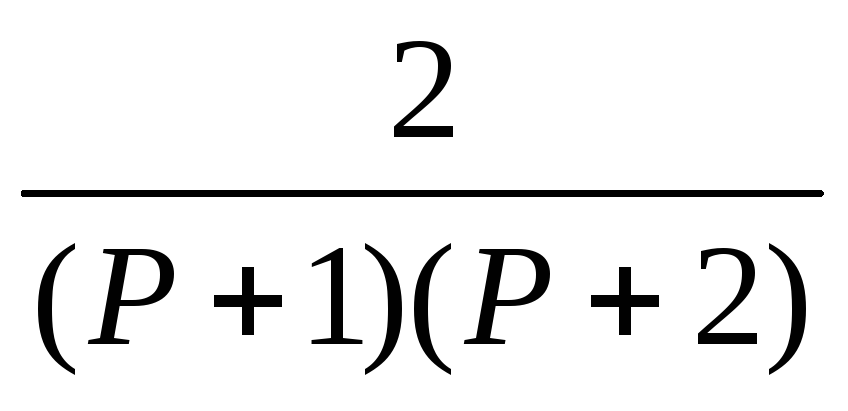 15.
15.
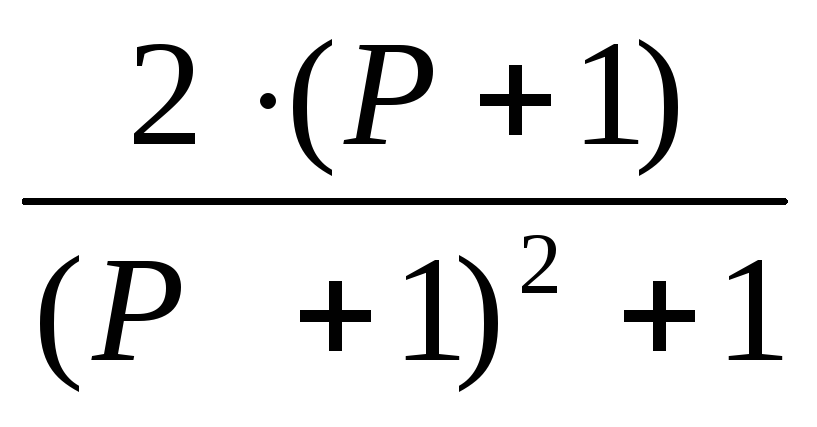
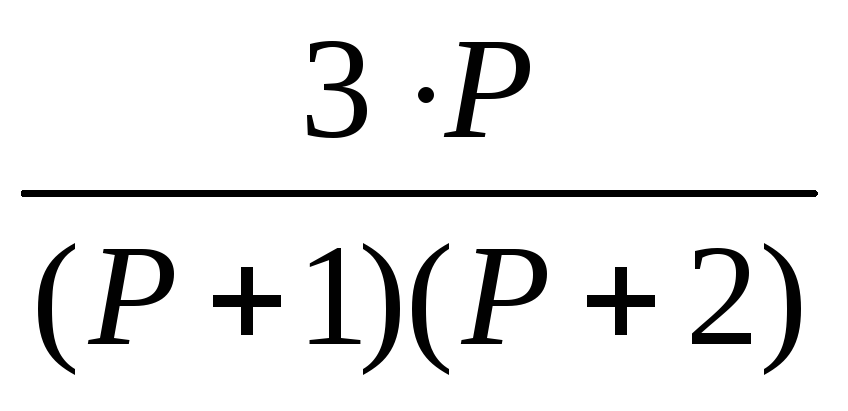 16
16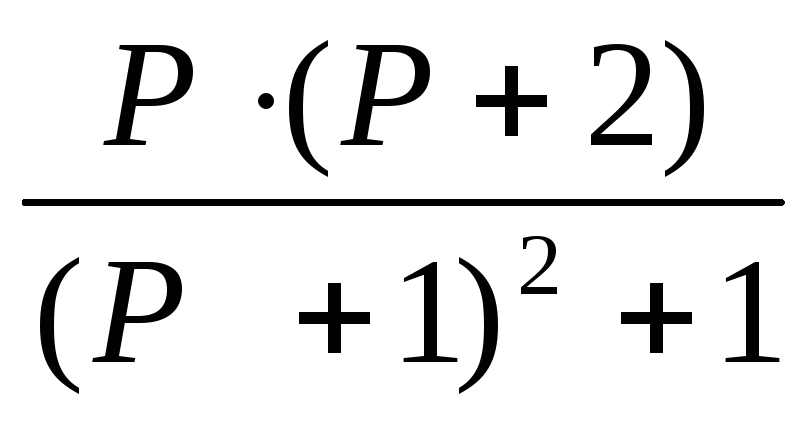
G. Диаграмма полюсов (*) и нулей (0) в комплексной частотной области ()
Примечание: по горизонтали – действительная ось-, по вертикали – мнимая ось-.
-



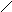





 1.
1. -1
-12.
-2 -1
3.
-2 -1
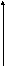

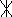
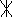


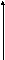

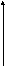

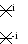
 4.
4.-3 -2 -1
5.
6.
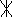
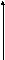



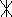


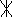
 7.
7.-1
-2
-i
8.
-2 -1
9.
-1


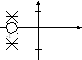 10.
10.-1
-i
11.
-1
-i
12.
i
-i

 13.
13.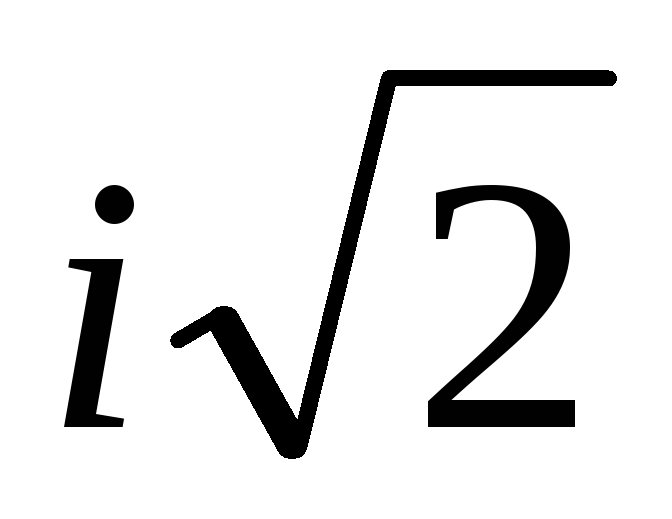
i
-1
-i
-
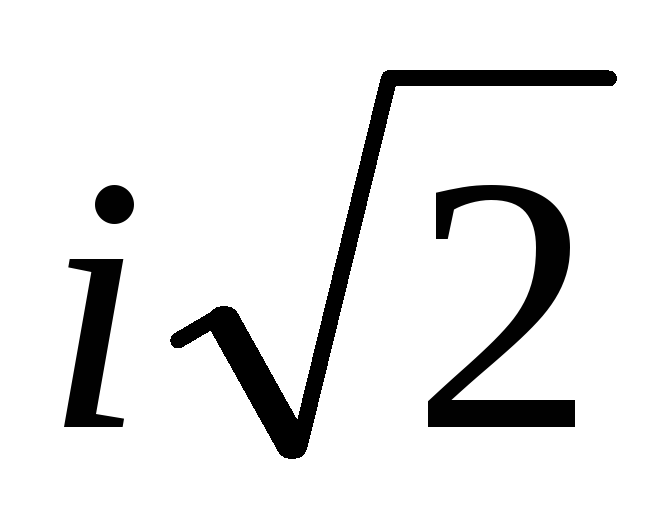
14.
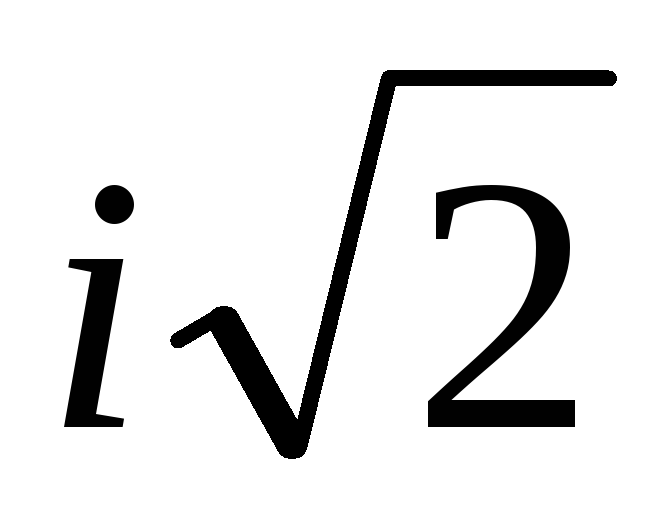
-
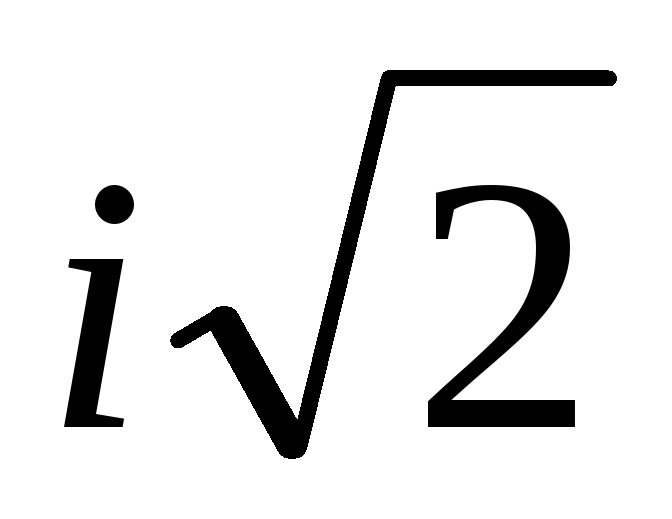
3. Рекомендации по решению задачи
Задача может быть строго решена классическими методами анализа, основываясь на элементарных сведениях из общей физики (законы Кирхгофа) и математики (линейные дифференциальные уравнения, комплексные числа, преобразование Лапласа). Однако этот классический анализ имеет свои недостатки: необходимость в математических выкладках, сложность которых быстро возрастает при усложнении системы, может служить источником ошибок как при аналитических, так и при машинных расчетах. Кроме того, этот метод неудобен в задачах синтеза - нахождение электрической, электронной или любой другой реализации системы по её свойствам.
Тем не менее, методы анализа могут быть полезны для проверки полученных решений, поэтому приведём их для одного из вариантов.
Для анализа целесообразно в качестве исходной характеристики выбрать электрическую схему.
Возьмём вариант D1. Входной сигнал (стимул) – X(t) представим в виде идеального источника напряжения с ЭДС, равной Е, а выходной сигнал в виде снимаемого с конденсатора напряженияUc .

![]() .
.
Так
как
![]() L
– отсутствует, то
L
– отсутствует, то
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() .
Окончательно получаем динамическое
уравнение, связывающее вход и выход
.
Окончательно получаем динамическое
уравнение, связывающее вход и выход![]() ,
что соответствует варианту Е1.
,
что соответствует варианту Е1.
Если
полученное уравнение записать в виде
![]() ,
легко определить структурную схему:x
складывается с (-y),
а потом интегрируется, следовательно,
это схема С1.
,
легко определить структурную схему:x
складывается с (-y),
а потом интегрируется, следовательно,
это схема С1.
Запишем интегральное уравнение в операторной форме.
Замечание 1 - некоторые соотношения преобразования Лапласа, связывающие оригинал с изображением
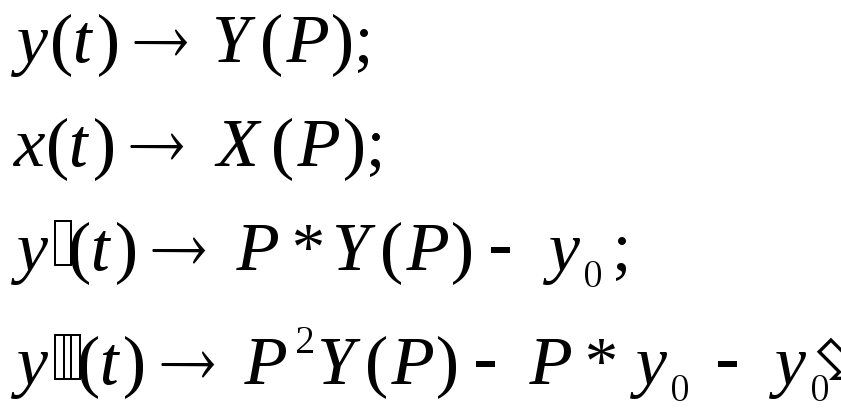
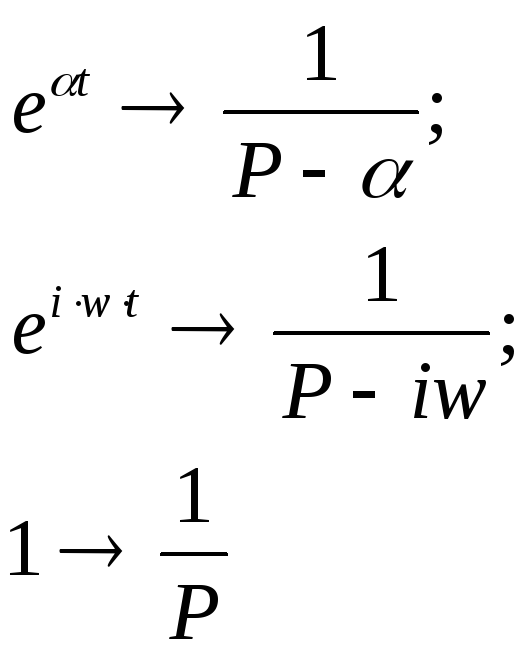
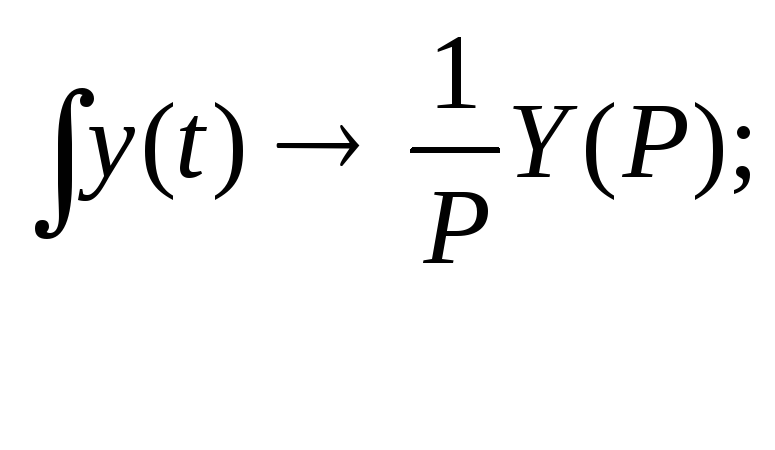
В
нашем случае
![]() или
или![]() .
Для нахождения системной функции,
связывающей вход и выход в операторной
форме, можно не учитывать
.
Для нахождения системной функции,
связывающей вход и выход в операторной
форме, можно не учитывать![]() и т.д. Системная функция при нулевых
начальных условиях
и т.д. Системная функция при нулевых
начальных условиях![]()
![]() .
Следовательно, это вариант F1.
.
Следовательно, это вариант F1.
При
![]() ,
следовательно, полюс
,
следовательно, полюс![]() .
В нольH
не обращается, т.е. нулей системная
функция не имеет. Окончательно диаграмма
полюсов и нулей в комплексной области
имеет вид:
.
В нольH
не обращается, т.е. нулей системная
функция не имеет. Окончательно диаграмма
полюсов и нулей в комплексной области
имеет вид:
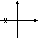
Следовательно, это вариант G1.
Найдём y(t) при x(t)=1 и при x(t)=0.
Отклик цепи (собственную реакцию, общее решение однородного уравнения (ОРОУ)) найдем, подставляя в уравнение y=ekt, получаем ekt(k+1)=0, откуда k=-1, ОРОУ у= e-t.
Вынужденную реакцию (частное решение неоднородного уравнения (ЧРНУ)) найдём методом подбора. При x=1 ЧРНУ y=1 , при x=0 ЧРНУ y=0. Действительно, легко убедиться, что решение y=1 удовлетворяет уравнению y'+y=1. Окончательная реакция равна сумме ОРОУ и ЧРНУ.
При
(0 < t < t![]() )
)![]() ,
так как
,
так как![]() .
.
При
![]()
![]() .
Для удобства перейдём к
.
Для удобства перейдём к![]() ,
тогда
,
тогда![]() будет соответствовать
будет соответствовать![]() =0,
=0,![]() . Решение получено. Легко определить,
что это вариант A1.
. Решение получено. Легко определить,
что это вариант A1.
Замечание 2: Для
уравнения второго порядка
![]() ,
ОРОУ также находится подстановкой
ekt.
,
ОРОУ также находится подстановкой
ekt.
При этом получается
характеристическое уравнение
![]() .
Пусть
.
Пусть![]() и
и![]() корни уравнения.
корни уравнения.
Если
![]() ,
,![]() .
.
Если![]() .
.
Если![]() комплексные
комплексные![]() .
.
Коэффициенты
![]() находятся из начальных условий y(0) и
y'(0), но после сложения ОРОУ и ЧРНУ.
находятся из начальных условий y(0) и
y'(0), но после сложения ОРОУ и ЧРНУ.
Если в правой части стоят члены x' и x", то для случая x=1 и x=0 x'=x"=0. В остальном решение других уравнений не отличается от приведенного выше решения уравнения y’+y=x.
Найдём
установившуюся (т.е. без учёта затухающих
членов) реакцию при
![]() .
Так как собственная реакция (ОРОУ)
большинства устойчивых систем носит
затухающий характер, то для определения
установившейся реакции достаточно
найти вынужденную реакцию системы
(ЧРНУ).
.
Так как собственная реакция (ОРОУ)
большинства устойчивых систем носит
затухающий характер, то для определения
установившейся реакции достаточно
найти вынужденную реакцию системы
(ЧРНУ).
Для
решения проще перейти к комплексным
переменным и положить
 .
В комплексных переменных получим
уравнение
.
В комплексных переменных получим
уравнение![]() .
Найдём ЧРНУ в виде
.
Найдём ЧРНУ в виде![]() :
:![]() ,
,![]() ,
,
![]() ,
где
,
где
![]() .
.
Тогда
![]() ,
,![]() ,
где
,
где![]() .
.
Амплитуда
A=1 при
![]() (
(![]() соответствует постоянному сигналу),при
соответствует постоянному сигналу),при![]() только при
только при![]() ,
т.е. при
,
т.е. при![]() функцияA()
не имеет экстремумов. Следовательно,
зависимость
функцияA()
не имеет экстремумов. Следовательно,
зависимость
![]() соответствует варианту В1.
соответствует варианту В1.
При
решении мы могли бы не вводить комплексные
числа, но тогда бы пришлось искать
решение в виде y=C1cost+C2sint,
определять коэффициенты С1
и С2
и преобразовывать окончательное
выражение к виду
![]() .
Следует также отметить, что для систем
без потерь (например, для электрических
схем, не содержащих сопротивлениеR)
при нахождении установившейся реакции
необходимо учитывать не только
вынужденную, но собственную реакцию
системы (ОРОУ).
.
Следует также отметить, что для систем
без потерь (например, для электрических
схем, не содержащих сопротивлениеR)
при нахождении установившейся реакции
необходимо учитывать не только
вынужденную, но собственную реакцию
системы (ОРОУ).
Итак, задача полностью решена. Сравнивая найденные характеристики, можно убедиться, что варианты A1,B1…G1 относятся к одной и той же системе. Однако даже для самой простой системы решение оказалось несколько трудоёмким, особенно для нахождения характеристик A и B. Вид A и B можно было получить, решая операторное уравнение Y*(p+1)=X+у(0). Это, как правило, оказывается проще, но требует определенного навыка решения уравнений операторным методом.
Попытаемся найти связь характеристик A,…,G путём рассуждений, опирающихся на понимание сути этих характеристик (это, собственно, и является целью данной работы). При этом оказывается возможным не только анализировать схемы, но и синтезировать их. Остановимся на том же варианте. Выбор исходной характеристики (A…или G) произвольный.
Можно
начать с дифференциального уравнения
или структурной схемы, связь между ними
устанавливается легко. Так же просто
находится системная функция и диаграмма
полюсов-нулей. Действительно, без учёта
начальных условий уравнение
![]() в
операторной форме имеет видpY+y=X,
следовательно,
в
операторной форме имеет видpY+y=X,
следовательно,
![]() ,
полюсp= -1.
,
полюсp= -1.
Если
начать с системной функции, то по виду
![]() находим уравненияPY+Y=X
и y'+y=x.
находим уравненияPY+Y=X
и y'+y=x.
Но
ещё интереснее в качестве исходной
характеристики выбрать диаграмму
полюсов и нулей, чтобы убедиться, как
много информации может содержать одна
точка в комплексной области. По полюсу
находится системная функция H=1/(p+1),
а затем дифференциальное уравнение и
структурная схема. Кроме того, полюсы
позволяют сравнительно просто найти
собственную реакцию системы. Если
имеется полюс p*
,то собственная реакция системы
![]() ,
гдеС
постоянная, определяемая из начальных
условий.
,
гдеС
постоянная, определяемая из начальных
условий.
Замечание3: Если
полюсов и нулей несколько, то H=![]() ,
где р01,
р02
– нули, p*1,
p*2
–полюса. При этом собственная реакция
системы
,
где р01,
р02
– нули, p*1,
p*2
–полюса. При этом собственная реакция
системы
![]() .
.
Если![]() ,
то
,
то![]() - собственная реакция затухает, система
устойчивая.
- собственная реакция затухает, система
устойчивая.
Если
![]() ,
то
,
то![]() система неустойчивая:
система неустойчивая:![]() при
при![]() .
.
Е![]() сли
сли![]() ,
то и собственная реакция имеет незатухающий
колебательный характер.
,
то и собственная реакция имеет незатухающий
колебательный характер.
Если
![]() (полюс не лежит на осях) , то
(полюс не лежит на осях) , то
![]() .
.
В зависимости от
знака
![]() реакция носит затухающий или нарастающий
колебательный характер.
реакция носит затухающий или нарастающий
колебательный характер.
Если внешний сигнал
подаётся на частоте, совпадающей с
полюсом p*,
то мы имеем резонанс: ярко выраженный
(при
![]() )
и слабо выраженный (при
)
и слабо выраженный (при![]() ),
совсем не выраженный в установившемся
режиме (при
),
совсем не выраженный в установившемся
режиме (при![]() ).
Если внешний сигнал подается на частоте,
совпадающей с нулем системной функции
Р0,
то система такой сигнал пропускать не
будет. Вынужденная реакция на стимул
).
Если внешний сигнал подается на частоте,
совпадающей с нулем системной функции
Р0,
то система такой сигнал пропускать не
будет. Вынужденная реакция на стимул
![]() будет
равна нулю. В частности, если p=0 , сигнал
y=1 не проходит через систему.
будет
равна нулю. В частности, если p=0 , сигнал
y=1 не проходит через систему.
С
учётом вышеизложенного легко находятся
характеристики A и B . Так как в нашем
варианте p*=-1,
собственная реакция
![]() ,то это могут быть варианты A1 и A3.
Отсутствие нуля в точкеp=0
однозначно свидетельствует в пользу
варианта A1. Реакция системы на ступенчатое
воздействие складывается из вынужденной
реакции y=1
и собственной реакции y=-e-t.
,то это могут быть варианты A1 и A3.
Отсутствие нуля в точкеp=0
однозначно свидетельствует в пользу
варианта A1. Реакция системы на ступенчатое
воздействие складывается из вынужденной
реакции y=1
и собственной реакции y=-e-t.
Для
нахождения характеристики B
(амплитудно-частотной характеристики)
учтём, что система не резонансная, т.к.
все полюса лежат на действительной оси.
Следовательно, это B1 или B2 – характеристики,
не имеющие локальных экстремумов.
Система пропускает постоянный сигнал
с
![]() (нет нуля приp=0),
следовательно, наш вариант B1.
(нет нуля приp=0),
следовательно, наш вариант B1.
Если
характеристику A выбрать в качестве
исходной, то легко выделить собственную
реакцию. Так как
![]() приx=1
и
приx=1
и
![]() приx=0,
следовательно, собственная реакция
приx=0,
следовательно, собственная реакция
![]() .
Полюс системной функцииp*=-1,
нулей (во всяком случаи при p=0)
нет. Далее мы можем повторить всё в
обратном направлении и определить
остальные характеристики.
.
Полюс системной функцииp*=-1,
нулей (во всяком случаи при p=0)
нет. Далее мы можем повторить всё в
обратном направлении и определить
остальные характеристики.
Если мы возьмём за исходный вариант характеристику В, то также найдём все остальные характеристики. При этом может получиться неоднозначность: несколько систем могут соответствовать одной амплитудно-частотной характеристике. Однако мы всё равно ответим на вопрос: "Какие системы обеспечивают выбранную зависимость амплитуды от частоты гармонических стимулов?".
Для нахождения электрической схемы исключим все схемы, содержащие одновременно L и C, так как их одновременное наличие приводит к производной второго порядка. Останется 4 схемы D1,D4,D5 и D6. Исключим две, не пропускающие постоянный сигнал. Останутся опять две схемы – D1 и D5. Вариант D1 среди них, но подходят обе схемы.
Если
начать с анализа схем, можно использовать
операторные сопротивления
![]() ,
связывающие ток и напряжение в операторной
формеU=ZI.
При этом мы избавимся от интегралов и
производных:
,
связывающие ток и напряжение в операторной
формеU=ZI.
При этом мы избавимся от интегралов и
производных:
![]() .
.
Учитывая,
что
![]() ,
т.е.
,
т.е.![]() ,
получаем
,
получаем![]() - уравнение в операторной форме. Далее
можно действовать по приведённой выше
методике.
- уравнение в операторной форме. Далее
можно действовать по приведённой выше
методике.
На устойчивость системы указывают многие факторы: затухающая реакция, отсутствие положительных обратных связей, отсутствие активных элементов в электрической схеме, отсутствие полюсов в правой плоскости и т.д.
Найти аналогичную систему из разных областей проще по характеристике A, т.е. виду y(t)при ступенчатом воздействии, или по характеристике В -амплитудно-частотной зависимости. В частности, электрический аналог данной системы - фильтр низких частот.
Форма отчетности.
Отчет должен содержать следующие разделы:
1. Задание с указанием вида характеристики и её конкретный вид (например, D1).
2. Ответ с указанием вида других характеристик (например, A1, B1, C1, E1, F1, G1).
3. Пояснения к решению задания (см. раздел 3 настоящего пособия).
4. Выводы об устойчивости системы.
5. Примеры аналогичных систем из различных областей науки и техники.
Литература.
1. Сиберт У.М. Цепи, сигналы, системы. Ч.1: Пер. с англ. М. : Мир, 1988. 336 с.
2. Терентьев А.А. Аналоговое моделирование физических систем. Саратов. СГТУ. 2000. 88 с.
АНАЛИЗ И СИНТЕЗ
НЕПРЕРЫВНЫХ СИСТЕМ
Методические указания
к выполнению лабораторных работ
Составил: ТЕРЕНТЬЕВ Александр Александрович
Рецензент: В.И. Вислов
Редактор: Л.А. Мишина
Лицензия ЛР № 020271 от 12.11.91
Подписано в печать Формат 60х84 1-16
Бум. оберт. Усл.-печ. л. Уч.-изд. л.
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054 г. Саратов, ул. Политехническая, 77
Ротапринт СГТУ, 410054 г. Саратов, ул. Политехническая, 77
