Лекция 7

ЛЕКЦИЯ 7. СИСТЕМЫ С ОБРАТНЫМИ СВЯЗЯМИ,

ПОЛОЖИТЕЛЬНЫЕ ОБРАТНЫЕ СВЯЗИ

7.1. Сложные системы, системы с обратными связями

О 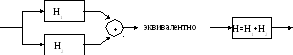т анализа одиночных систем перейдём к анализу систем, состоящих в свою очередь из подсистем. Объединение нескольких систем в одну обычно не представляет большой сложности, если уравнение, связывающее вход и выход (стимул и реакцию), записано в операторной форме.

Наиболее интересный случай, когда связи в системе образуют замкнутые петли, так называемые, обратные связи (ОС). Системой с обратными связями называется система, в которой выходной сигнал или его часть подаётся на вход, т. е. реакция или часть реакции является одновременно и стимулом.

П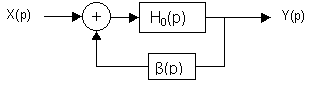 усть имеется система, её системная функция – H₀(p). Охватим её петлёй обратной связи.

H₀ – системная функция собственно системы, не охваченной обратной связью. Сама обратная связь тоже может представлять собой некоторую систему, имеющую системную функцию β(p), но чаще β(p) – это число, меньше единицы, показывающее, какая часть выходного сигнала подаётся на вход.

Если выход Y, то на вход поступает дополнительный сигнал βY. Хотя в общем случае сигналы X(p) и β(p)Y(p) могут складываться произвольным способом (например, две синусоиды, сдвинутые по фазе), в большинстве случаев можно выделить два предельных и наиболее распространенных случая.

Положительные ОС. Если часть выходного сигнала, подаваемая на вход, увеличивает входной сигнал, то такая обратная связь называется положительной. Таким образом, на вход подается сигнал (X + βY), например, для синусоид это означает, что они находятся «в фазе».

Отрицательные ОС. Если часть выходного сигнала, подаваемого на вход, уменьшает выходной сигнал, то такая обратная связь называется отрицательной. Таким образом, на вход подается сигнал (X – βY), для синусоидальных сигналов это означает, что они находятся «в противофазе».

Анализ систем в частотной области проводится применительно к операторной форме записи, т. е. для системной функции. Однако весь анализ будет справедлив и во временной области в обычных терминах x(t) и y(t), если связь между y и x можно представить в виде y=k₀x (т. е. система является усилителем с коэффициентом усиления k).

k₀ – показывает, как сама система усиливает сигнал;

β – показывает, какая часть выходного сигнала подаётся на вход.

В зависимости от ситуации, мы будем анализировать систему то во временной, то в частотной области.

7.2. Положительные обратные связи

Рассмотрим системы с положительными обратными связями (ПОС).

Итак, на входе X+βY. На выходе: (X + β Y) H₀ = Y, или Y = H₀ X / (1-H₀ β ).

Получаем новую систему: Y(P)=H(P)X(P), где .

Е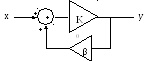сли система представлена в виде усилителя,

^то , ^или , ^где .

Сделаем общие выводы относительно влияния ПОС на свойства системы.

1. Наличие ПОС увеличивает усилительные свойства системы.

Пример. Пусть K₀=10, β=0.09 (т. е. 9% входного сигнала подаётся на вход): . Коэффициент усиления увеличился в 10 раз. Случай пока рассматривать не будем.

2. ПОС может привести систему в неустойчивое состояние. Это связано с тем, что «новая» системная функция может иметь полюса в положительной полуплоскости диаграммы полюсов и нулей.

Пример. Пусть , это - устойчивая система, полюс равен –1, собственная реакция . Охватим систему положительной обратной связью с β=0.5. Получим: 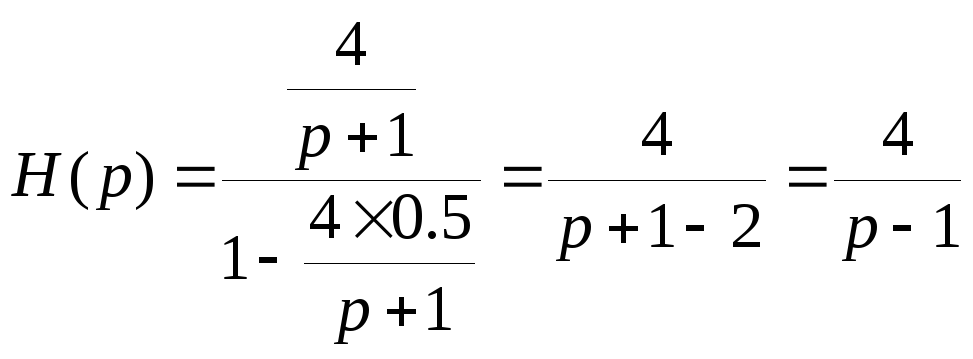Полюс p*=1, собственная реакция е^+t, следовательно, система стала неустойчивой.

Но если уменьшить коэффициент усиления или ослабить обратную связь система остается устойчивой.

Например, , .

Или , .

В обоих случаях система осталась устойчивой.

Вывод: Для того, чтобы ПОС превратила устойчивую систему в неустойчивую необходимо, чтобы коэффициент усиления был достаточно большим, а обратную связь достаточно сильной.

7.3. Генератор как усилитель с ПОС

Достаточно сильная ПОС может превратить усилительную систему в генерирующую. Пустьили .

В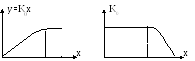 действительности случай β>1/H не реализуется. Как только становится ^β=1/K₀ ^{, стремится к бесконечности. Это приводит или к разрушению системы} или к уменьшению коэффициента усиления K₀.

Невозможно создать систему, имеющую постоянный коэффициент усиления K₀ при любом входном сигнале. Рано или поздно наступает насыщение, т. е. K₀=const только в определённых пределах. В экономических задачах это связано, например, с насыщением рынка (ограниченное число покупателей).

Итак, если , это приводит к росту суммарного входного сигнала и в конечном итоге к уменьшению K₀. Система стабилизируется.

В этом случае x<<βy, система продолжает работать, если на вход не подавать входной сигнал. При этом устанавливается режим, при котором x=0, а βK₀=1, коэффициент усиления равен бесконечности. Поэтому в этом случае не используют понятие коэффициента усиления.

При x=0 получаем систему, изображённую на рисунке:

Вход βy, выход y=βK₀y, следовательно, βK₀=1 – условие, необходимое для установления стационарного состояния генерации.

Увеличение β уменьшает 1/β (движение на графике вправо), и генерация устанавливается на более высоких значениях выходного сигнала. Уменьшение β увеличивает 1/β (движение на графике влево), генерация устанавливается на более низких значениях выходного сигнала. Если β<1/K_{0 max} , генерация не получится совсем.

Необходимые условия генерации:

1) K₀>1, т. е. система должна быть активной (содержать источник энергии), т. е. усиливать входной сигнал;

2) ПОС должна быть достаточно большой β>1/K_{0 max}.

Таким образом, можно считать, что любой генератор – это усилитель с положительной обратной связью.

7.4 Возбуждение генератора

Рассмотрим теперь вопрос о том, как генератор может начать работу.

Пусть в начальный момент времени y=0 и x=0, т. е. входного сигнала нет и нет ещё выходного сигнала. Как начнёт работать генератор? Откуда возьмётся сигнал в первый момент? Возможно два способа возбуждения.

Генератор с мягким возбуждением. Вначале может возникнуть какой-то случайный сигнал за счёт «шума» (например, при подключении системы к источнику питания). Очень маленький входной сигнал начнёт усиливаться за счёт ПОС, из шума выделится сигнал, для которого обеспечивается ПОС, и система самовозбудится.

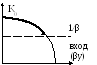
Генератор с жёстким возбуждением. Если при маленькой амплитуде на выходе (и, следовательно, на входе) коэффициент усиления маленький, например, за счёт больших потерь, генератор сам не сможет возбудиться.

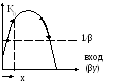
Для возбуждения системы необходимо в начальный момент подать входной сигнал x, который, после того как система преодолеет определённый рубеж, можно отключить.

4