Лекция 6. Моделирование в частотной области

Упростить анализ систем удаётся при помощи операторного метода (преобразования Лапласа). При этом дифференциальные уравнения заменяются на алгебраические уравнения относительно переменной, называемой комплексной частотой. В результате анализ систем существенно упрощается и в ряде случаев сводится к формальным процедурам.

6.1 Преобразования Фурье

Первая теорема Фурье: Любой периодический процесс (сложную периодическую функцию) можно представить как сумму гармонических процессов, то есть как суперпозицию синусоидальных колебаний (сумму синусов и косинусов или комплексных экспонент).

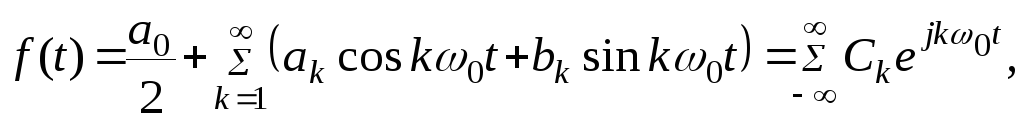где, 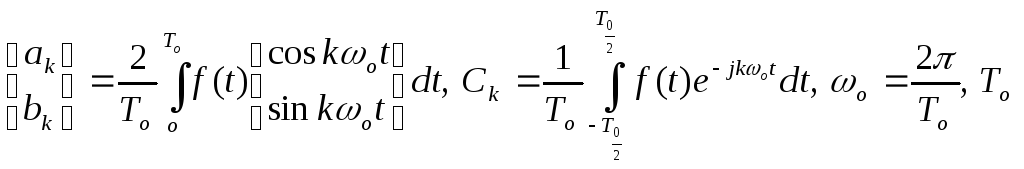– период.

Можно без преувеличения сказать, что на этом представлении основана вся радиотехника. Вместо сигнала сложной формы говорят о наборе гармоник, например, «высокие частоты», «низкие частоты». Хотя речь идет не о гармоническом колебании, а о сигнале сложной формы, который мы искусственно разбиваем на набор гармоник.

Например, импульсный режим можно представить в следующем виде.

Анализ процессов во временной области заменяется анализом в частотной области. Получаем дискретный спектр: частоты, амплитуды и фазы гармоник.

Успехи анализа периодических процессов в частотной области привели к обобщению этого метода и на непериодические процессы. Интегралы Фурье получаются из рядов Фурье, если устремить период к бесконечности.

Вторая теорема Фурье: произвольную функцию можно представить в виде интеграла от функции , называемой спектральной плоскостью.

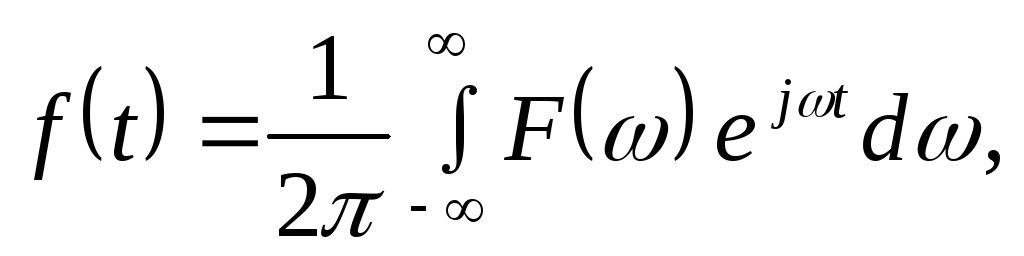где .

При этом вместо дискретного спектра (набора гармоник) получаем непрерывный спектр , например, см. пунктирную линию на рисунках.

2. Преобразование Лапласа

Однако преобразование Фурье обладают следующими недостатками.

1. На функцию накладываются жесткие требования. Необходимо чтобы функциястремилась к нулю прии чтобы интеграл от(то есть отили) сходился.

2. При вычислении интеграл во времени берется отдо. А поведение функции приt0 мы не знаем. У нас только информация о поведении системы с момента t=0, то есть в преобразовании Фурье не учитываются начальные условия. Поэтому Лапласом была предложена модификация преобразования Фурье. Интеграл берется не от , а от функции

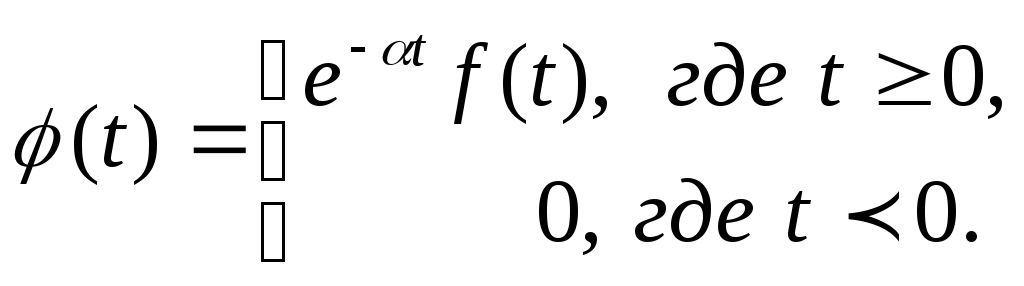
Таким образом, подынтегральное выражение принимает вид гдеи требование к сходимости функциистановиться менее жесткими, т.к. интеграл берется от функции, умноженной на быстро убывающий (при) сомножитель. Кроме того, интеграл берет от нуля, то есть учитываются начальные условия при

, .

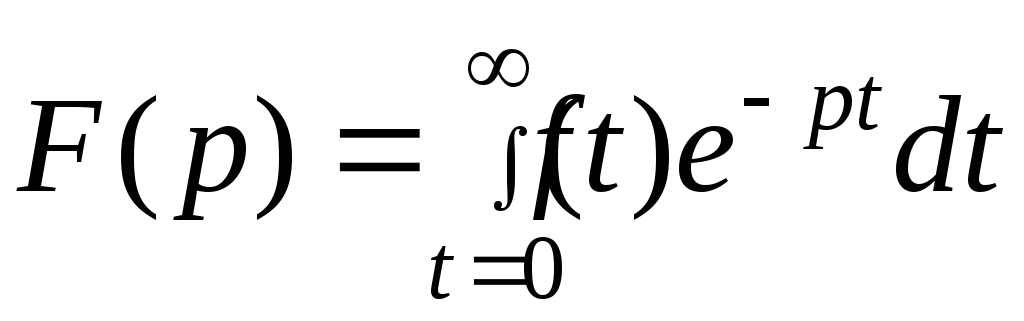
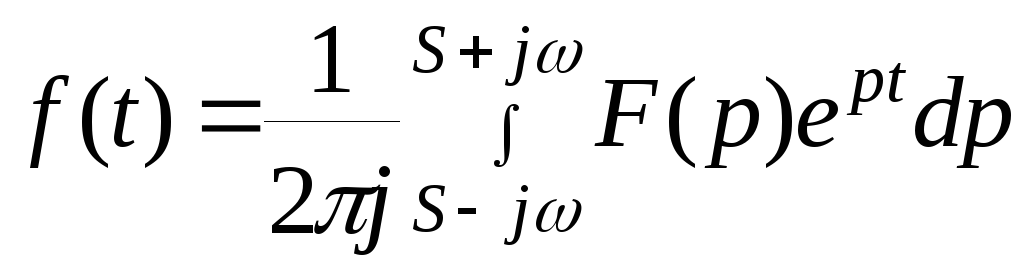Функция f(t) называется оригиналом, а F(p) - изображением. Интеграл вычисляется просто, но еще проще пользоваться таблицей.

Преобразования Лапласа позволяют функции f(t) поставить в соответствие F(p) и наоборот, причём это соответствие взаимно- однозначное.

Пользуясь свойством линейности, можно получить суперпозиции большинства элементарных функций. В итоге вместо частоты в привычном понимании - ω получается комплексная частота p=S+jω.

Но главное: преобразования Лапласа позволяют свести дифференциальных уравнений к алгебраическим.

Если изображением f(t) является F(p) ( f(t)→F(p)), то

_, .

Моделирование системы в частотной области имеет определенные преимущества по сравнению с моделированием во временной области.