Пример

Пример.

У фермера 24 га свободной земли. Цель – получить максимальный доход.

Можно выращивать быстро растущие ели, время роста 1 год, продажа партиями в 1000 штук по цене 2.5 у. е. за дерево, издержки для одной партии: требуется 1.5 га земли, 20 часов времени и 150 у.е. в год.

Можно использовать землю под пастбище, выращивать бычков и продавать их через год за 5000 у.е. Издержки на одного бычка: 4 га земли, 20 часов времени и затрат 1200 у.е. в год. Но уже заключен контракт на 2 бычка.

Фермер не может тратить более 200 часов и 6000 у.е. в год.

Переменные: - количество бычков, - количество партий елей.

Показатель эффективности (целевая функция) – доход за год

. Необходимо, чтобы - была максимальной.

Ограничения:

по земле

по бюджету

по времени

по обязательствам

естественные ограничения

Вернемся к примеру и запишем условия в стандартной форме

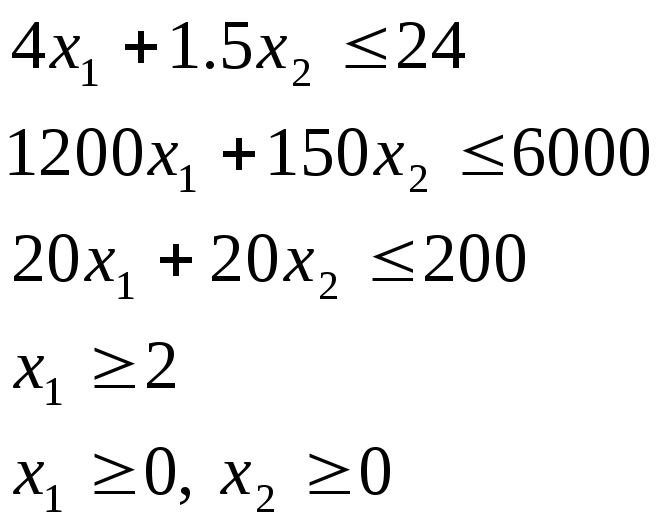
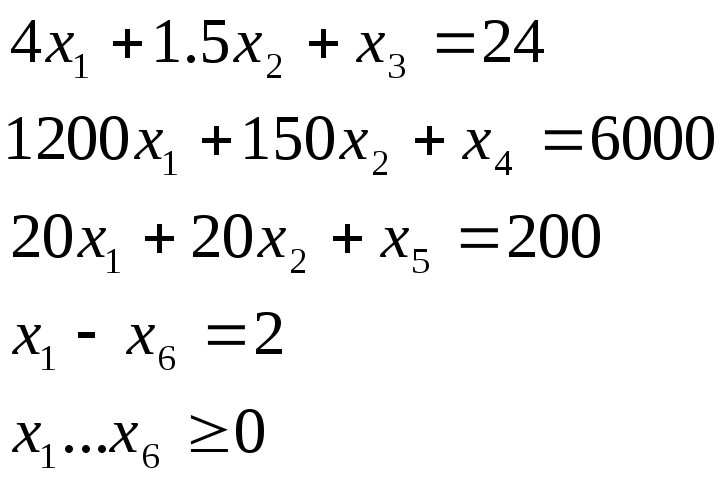
1. Выбираем начальное допустимое базисное решение при нулевых значениях не базисных переменных. При этом

Заполняем первоначальную таблицу симплекс метода (без последней строки и последнего столбца).

Cb	Xб	X1	X2	X3	X4	X5
0	X3	4	1,5	1	0	0	24
0	X4	1200	150	0	1	0	6000
0	X5	20	20	0	0	1	200
C-строка				0	0	0	W max

В первом столбце указываются коэффициенты в выражении для целевой функции, но только для базисной переменной (как правило в начальный момент базисными являются дополнительные переменные, не входящими в целевую функцию, поэтому коэффициенты оказываются равными нулю).

2. Вычисляем вектор относительных оценок ̃:

̃_j = номер столбца, номер строки.

где номер переменной (и соответствующего столбца), для которой ищется относительная оценка _j̃ ;

- значение коэффициента в выражении для целевой функции перед переменной ;

- значения коэффициентов в целевой функции, но только для базисной переменной (т.е. левый столбец);

-ый столбец коэффициентов т.е. тот столбец, для которого ищется _j̃ ;

Заполняем - строку (относительные оценки _j̃ ), в правом нижнем углу указываем значения целевой функции

Следует отметить, что для базисных переменных ̃_j

т.к. при < ̃_j =

Cb	Xб	X1	X2	X3	X4	X5
0	X3	4	1,5	1	0	0	24
0	X4	1200	150	0	1	0	6000
0	X5	20	20	0	0	1	200
C-строка	W	5000	2500	0	0	0	max

3. Если все оценки ̃_j то текущее решение обеспечивает максимальное значение целевой функции, и задача максимума решена (т.е. в задачах необходимо сделать все значения строки неположительными).

Если все оценки ̃_j то текущее решение обеспечивает минимальное значение целевой функции, и задача минимума решена (т.е. в задачах необходимо сделать все значения строки неотрицательными).

В противном случае переходим к этапу 4.

4. Определяем переменную для которой относительная оценка ̃_j

-максимальная (если решается задача максимума ),

-минимальная (если решается задача минимума ).

Эту переменную надо сделать базисной, чтобы она входила только в одно уравнение с коэффициентом +1.

5. Определяем базисную переменную которую из базисной надо перевести в свободные.

Для этого определяем столбец , где номер строки, номер столбца переменной , которую будем переводить в базисную (таким образом, свободные члены делим на коэффициенты перед переменной ).

Выбираем минимальное положительное значение отрицательные значения в выборе не участвуют, их как бы считают бесконечно большими.

По строке (например ) определяет переменную , которую будет переводить из базисной в свободные переменные.

	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B	B/A
0	х3	4	1,5	1	0	0	24	6
0	x4	1200	150	0	1	0	6000	5
0	x5	20	20	0	0	1	200	10
C-строка		5000	2500	0	0	0	W=	0

. Преобразуем уравнение так, чтобы новая базисная переменная входила только в одно уравнение с коэффициентом +1 (при этом переменная может входить в любое уравнение с произвольными коэффициентами).

	4	1.5	1	0	0	24
	1200	150	0	1	0	6000
	20	20	0	0	1	200

Пусть по результатам - строки нам необходимо переменную перевести в базисную, а по результатам - столбца переменную надо сделать небазисной. Для этого необходимо сделать следующее.

1. Делим все строки (все коэффициенты и ) на , где - номер строки, - номер новой базисной переменной. Разделим все строки на

	1	3/8	1/4	0	0	6
	1	1/8	0	1/1200	0	5
	1	1	0	0	1/20	10

Теперь все коэффициенты перед равны единице.

2. Строку с номером оставляем без изменений и её вычитаем из остальных строк (эти действия позволяют добиться, чтобы переменная входила в одну строку, т.е. в одно уравнение, с коэффициентом +1).

Вычитаем вторую строку (соответствующую переменной ) из первой и третьей строки.

	0	1/4	1/4	-1/1200	0	1
	1	1/8	0	1/1200	0	5
	0	7/8	0	-1/1200	1/20	5

Теперь базисной стала переменная т.к. входит только в одно уравнение (во вторую строку) с коэффициентом +1. Поэтому вторая строка будет соответствовать новой базисной переменной (а не ).

Однако другие базисные переменные () входят в уравнения с коэффициентами, отличными от +1.

3. Делим все строки (кроме строки с номером ) на , где - номер строки, соответствующей базисной переменной (это позволяет добиться, чтобы остальные базисные переменные входили в уравнении (строки) с коэффициентами +1).

Делим первую и третью строки на (первую на , третью на ).

	0	1	1	-1/300	0	4
	1	1/8	0	1/1200	0	5
	0	35/2	0	-1/60	1	100

Теперь базисные переменные входят только в одну сторону с коэффициентом +1, и все >.

4. Проверяем, что и все . Теперь переменная становится базисной, а переменная становится не базисной.

Далее можно вначале расположить базисные переменные.

Строки так же можно расположить в порядке возрастания индекса.

Составляем новую симплекс-таблицу и переходим к пункту 2 (определяет строку). Вычисления повторяются до тех пор, пока все значения строки станут неположительными (в задачах максимума) или неотрицательными (в задачах минимума).

Результат 1 шага
	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B	B/A
0	x3	0	1	1	-0,003	0	4	4
5000	x1	1	0,125	0	0,0008	0	5	40
0	x5	0	17,5	0	-0,017	1	100	5,7143
C-строка		0	1875	0	-4,167	0	W=	25000