Двухэтапный симплекс-метод Постановка задачи

Вначале рассмотрим пример с учетом ограничения

- максимум

Для представления задачи в каноническом виде мы ввели дополнительные переменные и и получили систему уравнений

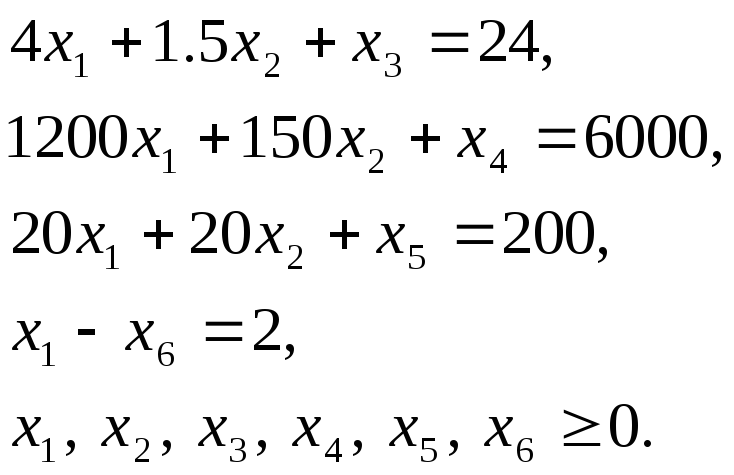
Однако система не приобрела канонического вида, так как входит в уравнение с коэффициентом  1. Действительно, если положить свободными переменными а остальные сделать базисными, то получим Так как оказалось, что  это не является допустимым базисным решением, и мы не можем использовать для решения симплекс-метод.

Для решения подобных задач используется метод искусственных переменных. Для этого введем искусственную переменную и запишем последнее уравнение в виде

Тогда переменную можно сделать свободной а базисной

Необходимо отметить, что переменная в отличие от других переменных не имеет какого-то значимого смысла (напомним, что показывают остаток ресурсов, а показывает на сколько значение превосходит заключенный контракт ). Поэтому в качестве первого этапа решения нам необходимо добиться обращения переменной в нуль. Это позволит нам получить допустимое начальное базисное решение для второго этапа – оптимизации целевой функции.

Алгоритм двухэтапного симплекс-метода

Для решения задачи ЛП запишем систему ограничений в стандартной форме, для чего все неравенства превращаем в уравнения вводя дополнительные переменные.

Если систему ограничений не удается записать в каноническом виде (так, что бы в каждое уравнение входили переменные с коэффициентом +1, и эти переменные не входили бы в другие уравнения) используем двухэтапный симплекс-метод.

Для этого в уравнения (в которых нет переменной входящей с коэффициентом +1 и не входящей в другое уравнение) вводим искусственные переменные с коэффициентом +1.

Этап 1. Вводится искусственная (дополнительная) целевая функция (например, ), равная сумме всех искусственных переменных, которая минимизируется с помощью симплекс-метода. Если минимальное значение вспомогательное, задачи (искусственной целевой функции ) равно нулю, то все искусственные переменные обращаются в ноль. Это позволяет получить начальное допустимое решение для основной задачи.

Этап 2. На втором этапе начальное допустимое базисное решение, полученное на первом этапе, улучшается в соответствие с целевой функции исходной задачи ЛП, то есть находится максимум или минимум основной целевой функцией обычным симплекс-методом. При этом искусственные переменные в преобразованиях не участвуют (они должны оставаться равными нулю и были введены только для получения начального допустимого базисного решения).

Пример

Введя искусственную переменную , получим

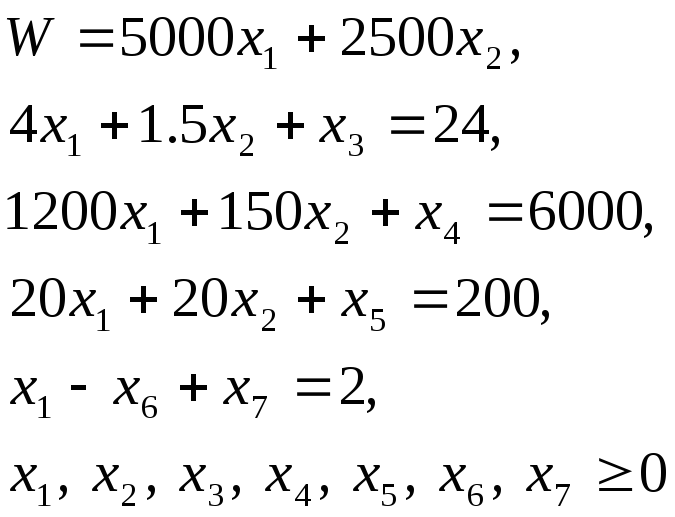
Базисные переменные ,

остальные переменные свободные (). На первом этапе вводим искусственную целевую функцию (так как у нас только одна искусственная переменная) и добиваемся минимума После её обращения в ноль переходим ко второму этапу – нахождение максимума исходной целевой функции

Результаты счета приведены в контрольном примере №2.

Контрольный пример №2
					Двухэтапный симплекс метод
	Целевая функция: W=5000*x1+2500*x2										max
Ограничения:		4*x1+1.5*x2≤24
		1200*x1+150*x2≤6000
		20*x1+20*x2≤200
		x1≥2
		x1,x2≥0
Этап 1.
Добавляем переменные x3,x4,x5,x6, превращая неравенства в уравнения.
Вводим искусственную переменную x7, целевую функцию W1=x7, решаем задачу min(W1)
Получим следующие коэффициенты в ограничениях и целевой функции:
	X1	X2	X3	X4	X5	X6	X7		B
	4	1,5	1	0	0	0	0		24
	1200	150	0	1	0	0	0		6000
	20	20	0	0	1	0	0		200
	1	0	0	0	0	-1	1		2
W1	0	0	0	0	0	1	0		min
Исходная таблица (столбец с минимальным значением C и строка
с минимальным значением B/A выделены серым цветом)
	W1	0	0	0	0	0	0		1	min
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B	B/A
0	x3	4	1,5	1	0	0	0		0	24	6
0	x4	1200	150	0	1	0	0		0	6000	5
0	x5	20	20	0	0	1	0		0	200	10
1	x7	1	0	0	0	0	-1		1	2	2
C-строка		-1	0	0	0	0	1		0	W1	2
Результат 1 шага
	W1	0	0	0	0	0	0		1	min
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B
0	x3	0	1,5	1	0	0	4		-4	16
0	x4	0	150	0	1	0	1200		-1200	3600
0	x5	0	20	0	0	1	20		-20	160
0	x1	1	0	0	0	0	-1		1	2
C-строка		0	0	0	0	0	0		1	W1	0
Вся C-строка содержит неотрицательные числа. Минимум W1 найден: W1=x7=0
Этап 2.		Нахождение максимума функции W=5000*x1+2500*x2
Искусственная переменная x7 и соответствующий столбец
(выделен черным цветом) в преобразования не участвуют
Исходная таблица (столбец с максимальным значением C и строка с минимальным значением B/A выделены серым цветом)
	W	5000	2500	0	0	0	0		0	max
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B	B/A
0	x3	0	1,5	1	0	0	4		-4	16	4
0	x4	0	150	0	1	0	1200		-1200	3600	3
0	x5	0	20	0	0	1	20		-20	160	8
5000	x1	1	0	0	0	0	-1		1	2	-2
C-строка		0	2500	0	0	0	5000		-5000	W=	10000
Результат 1 шага
	W	5000	2500	0	0	0	0		1	max
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B	B/A
0	x3	0	1	1	-0,003	0	0		0	4	4
0	x6	0	0,125	0	0,0008	0	1		-1	3	24
0	x5	0	17,5	0	-0,017	1	0		0	100	5,7143
5000	x1	1	0,125	0	0,0008	0	0		0	5	40
C-строка		0	1875	0	-4,167	0	0		1	W=	25000
Результат 2 шага
	W	5000	2500	0	0	0	0		1	max
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B	B/A
2500	x2	0	1	1	-0,003	0	0		0	4	-1200
0	x6	0	0	-0,125	0,0013	0	1		-1	2,5	2000
0	x5	0	0	-17,5	0,0417	1	0		0	30	720
5000	x1	1	0	-0,125	0,0013	0	0		0	4,5	3600
C-строка		0	0	-1875	2,0833	0	0		1	W=	32500
Результат 3 шага
	W	5000	2500	0	0	0	0		1	max
Cb	Xb	X1	X2	X3	X4	X5	X6		X7	B
2500	x2	0	1	-0,4	0	0,08	0		0	6,4
0	x6	0	0	0,4	0	-0,03	1		-1	1,6
0	x4	0	0	-420	1	24	0		0	720
5000	x1	1	0	0,4	0	-0,03	0		0	3,6
C-строка		0	0	-1000	0	-50	0		1	W=	34000
Вся C-строка содержит неположительные числа.
Максимум W найден. Задача решена
x1=3.6 x2=6.4 x4=720 x6=1.6 x3=x5=0 W=34000

Нетрудно видеть, что начальная точка первого этапа соответствует началу координат на графике а в результате одного шага мы переходим в точку А (см. рис. 1), то есть начальное допустимое значение соответствует - это результат первого этапа.

На втором этапе мы последовательно за три шага переходим в точки В, С и D, где . В принципе окончательная таблица не отличается от одноэтапного симплекс-метода, только в ней появляется переменная которая всегда на 2 меньше, чем

Теперь подведем итог и сформулируем методы решения задач ЛП симплекс-метода при произвольных ограничениях (равенств, неравенств).