Лекции 4

Алгоритм одноэтапного симплекс- метода

Пусть дана целевая функция и дана система ограничений в виде системы уравнений в каноническом виде:

…

– число переменных (из них m- базисных), – число ограничений.

1. Выбираем начальное допустимое базисное решение, получены при нулевых значениях не базисных переменных:

При этом

Заполняем первоначальную таблицу симплекс метода (без последней строки и последнего столбца).

В первом столбце указываются коэффициенты в выражении для целевой функции, но только для базисной переменной (как правило в начальный момент базисными являются дополнительные переменные, не входящими в целевую функцию, поэтому коэффициенты оказываются равными нулю).

В следующем столбце указываются базисные переменные, затем следуют коэффициенты в ограничениях (для базисных переменных, входящих только в одно уравнение коэффициенты единица и нули) и свободные члены

2. Вычисляем вектор относительных оценок ̃:

̃_j=

где номер переменной (и соответствующего столбца), для которой ищется относительная оценка _j̃ ;

- значение коэффициента в выражении для целевой функции перед переменной ;

- значения коэффициентов в целевой функции, но только для базисной переменной (т.е. левый столбец);

- -ый столбец коэффициентов т.е. тот столбец, для которого ищется _j̃ ;

т.е. ̃_j = номер столбца, номер строки.

Заполняем - строку (относительные оценки _j̃ ), в правом нижнем углу указываем значения целевой функции

Следует отметить, что для базисных переменных ̃_j

т.к. при < ̃_j =

3. Если все оценки ̃_j то текущее решение обеспечивает максимальное значение целевой функции, и задача максимума решена (т.е. в задачах необходимо сделать все значения строки неположительными).

Если все оценки ̃_j то текущее решение обеспечивает минимальное значение целевой функции, и задача минимума решена (т.е. в задачах необходимо сделать все значения строки неотрицательными).

В противном случае переходим к этапу 4.

4. Определяем переменную для которой относительная оценка ̃_j

-максимальная (если решается задача максимума ),

-минимальная (если решается задача минимума ).

Эту переменную надо сделать базисной, чтобы она входила только в одно уравнение с коэффициентом +1.

5. Определяем базисную переменную которую из базисной надо перевести в свободные.

Для этого определяем столбец , где номер строки, номер столбца переменной , которую будем переводить в базисную (таким образом, свободные члены делим на коэффициенты перед переменной ).

Выбираем минимальное положительное значение отрицательные значения в выборе не участвуют, их как бы считают бесконечно большими.

По строке (например ) определяет переменную , которую будет переводить из базисной в свободные переменные.

6. Преобразуем уравнение так, чтобы новая базисная переменная входила только в одно уравнение с коэффициентом +1 (при этом переменная может входить в любое уравнение с произвольными коэффициентами). Это делается с помощью алгебраических преобразований (алгоритм таких преобразований описан отдельно).

7. Составляем новую симплекс-таблицу и переходим к пункту 2 (определяет строку). Вычисления повторяются до тех пор, пока все значения строки станут неположительными (в задачах максимума) или неотрицательными (в задачах минимума).

i=1..m j=1..n

базис

X1

X2

…

Xm

Xm+1

…

Xk

…

Xn

bi

di

C1баз

X1

1

0

0

0

a1,m+1

a1,k

a1,n

b1

d2

C2баз

X2

0

1

0

0

a2, m+1

a2,k

a2,n

b2

d1

Min

…

Ceбаз

Xe

0

0

0

ae, m+1

ae,k

ae,n

be

de

…

Cmбаз

Xm

0

0

0

1

am, m+1

am,k

am,n

bn

dn

C- строка

0

0

0

0

Čm+1

Čk

Čn

W=

базисные небазисные

Max

(Min)

Таблица симплекс метода

Пример

Вернемся к рассмотренному примеру и решим его с помощью симплекс-метода. При этом будем считать, что ограничение по контракту отсутствует. Это позволит нам использовать одноэтапный симплекс-метод.

Решение представлено в контрольном примере №1. Результат получен непосредственно из программы расчетов, но для удобства решение снабжено необходимыми комментариями.

Вначале приводится целевая функция и ограничения, потом вводится дополнительные (избыточные) переменные. Затем составляется симплекс-таблица и проводится решение.

Следует отметить, что таблица программной реализации несколько отличается от таблицы, приведенной при описании алгоритма симплекс-метода:

• в нее добавлена строка с коэффициентами целевой функции (которая, кстати, не меняется по шагам и её присутствие в таблице не обязательно);

• в ней столбцы с переменными 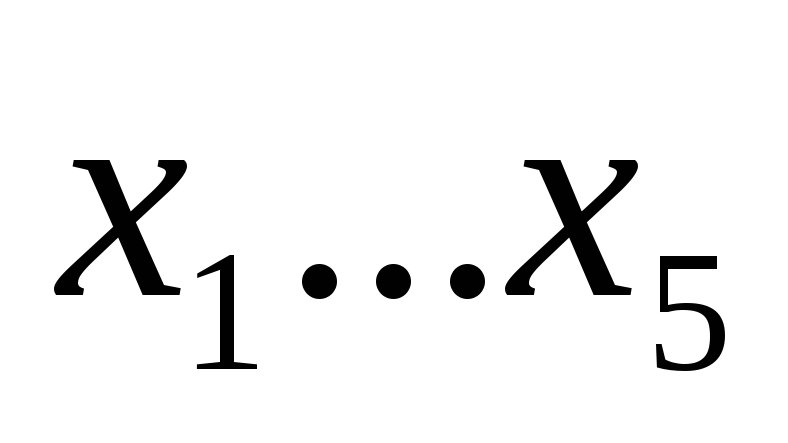расположены по возрастанию порядкового номера и их расположение не меняется от шага к шагу (т.е. базовые переменные не вынесены в начало таблицы).

Начальная симплекс-таблица соответствует 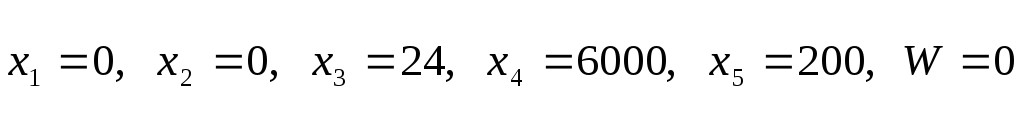, т.е. началу координат на рис.1. По результатам с-строки и столбца приходим к выводу, что должна стать базисной, а свободной.

Далее за три шага мы попадем соответственно в следующие точки рисунка 1:

- точка В ();

- точка С ;

- точка D .

Это и есть оптимальное решение При этом (земля и время расходуются полностью), (остаток денег). Так как все с-строки содержит не положительные числа, задача максимума решена.

В заключении приведем также методику перевода базисной переменной в свободную, а свободную переменную в базисную.

Контрольный пример №1
				Одноэтапный симплекс метод
Целевая функция: W=5000*x1+2500*x2								max
Ограничения:		4*x1+1.5*x2≤24
		1200*x1+150*x2≤6000
		20*x1+20*x2≤200
		x1,x2≥0
Добавляем переменные x3,x4,x5, превращая неравенства в уравнения.
		X1	X2	X3	X4	X5
		4	1,5	1	0	0	24
		1200	150	0	1	0	6000
		20	20	0	0	1	200
	W	5000	2500	0	0	0	max
Исходная таблица (столбец с максимальным значением C и строка
с минимальным значением B/A выделены серым цветом)
	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B	B/A
0	х3	4	1,5	1	0	0	24	6
0	x4	1200	150	0	1	0	6000	5
0	x5	20	20	0	0	1	200	10
C-строка		5000	2500	0	0	0	W=	0
Результат 1 шага
	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B	B/A
0	x3	0	1	1	-0,003	0	4	4
5000	x1	1	0,125	0	0,0008	0	5	40
0	x5	0	17,5	0	-0,017	1	100	5,7143
C-строка		0	1875	0	-4,167	0	W=	25000
Результат 2 шага
	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B	B/A
2500	x2	0	1	1	-0,003	0	4	-1200
5000	x1	1	0	-0,125	0,0013	0	4,5	3600
0	x5	0	0	-17,5	0,0417	1	30	720
C-строка		0	0	-1875	2,0833	0	W=	32500
Результат 3 шага
	W	5000	2500	0	0	0	max
Cb	Xb	X1	X2	X3	X4	X5	B
2500	x2	0	1	-0,4	0	0,08	6,4
5000	x1	1	0	0,4	0	-0,03	3,6
0	x4	0	0	-420	1	24	720
C-строка		0	0	-1000	0	-50	W=	34000
	Вся C-строка содержит неположительные числа.
	Максимум W найден. Задача решена
	x1=3.6 x2=6.4 x4=720 x3=x5=0 W=34000