ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Задачами линейного программирования (ЛП) называются задачи, в которых целевая функция и ограничения в виде равенств и неравенств линейные и которые не могут быть решены методами алгебры. При этом имеется в виду, что состояние системы детерминировано и не меняется со временем, а целевая функция скаляр.

К задачам ЛП относятся задачи рационального использования сырья и материалов, оптимизации раскроя, оптимизация плана перевозок, размещения и организации производства и многие другие. Как уже отмечалось, ЛП – наиболее часто используемый метод оптимизации.

Изучение методов ЛП начнем с рассмотрения конкретного примера.

Пример. У фермера 24 га свободной земли. Цель – получить максимальный доход.

Можно выращивать быстро растущие ели, время роста 1 год, продажа партиями в 1000 штук по цене 2.5 у. е. за дерево, издержки для одной партии: требуется 1.5 га земли, 20 часов времени и 150 у.е. в год.

Можно использовать землю под пастбище, выращивать бычков и продавать их через год за 5000 у.е. Издержки на одного бычка: 4 га земли, 20 часов времени и затрат 1200 у.е. в год. Но уже заключен контракт на 2 бычка.

Фермер не может тратить более 200 часов и 6000 у.е. в год.

Вопрос – что фермеру делать?

Постановка задачи

Переменные: - количество бычков, - количество партий елей.

Показатель эффективности (целевая функция) – доход за год

. Необходимо, чтобы - была максимальной.

Ограничения:

по земле

по бюджету

по времени

по обязательствам

естественные ограничения

Эта задача линейного программирования: все уравнения линейны, все связи детерминированы и не меняются со временем, показатель эффективности – одноцелевая функция. Кроме того, она достаточно сложна, так как в реальной ситуации необходимо было бы еще учесть, что и - целые числа.

Геометрическая интерпретация задач ЛП

(графическое решение задач ЛП)

В координатах определим область допустимых значений. Для этого построим прямые, получаемые из ограничений – неравенств.

или

или

или

На построенных линиях уравнения являются равенствами, а нам нужны неравенства. С одной стороны правая часть больше левой, с другой меньше. Определим для каждого ограничения допустимую область (справа или слева), а потом найдем их пересечение. Получим область допустимых значений.

Замечание: Для определения справа или слева можно подставить пробные значения. Например, для и  начало координат соответствует области . Следовательно, надо брать сторону, не содержащую начало координат. Для  и  определить область еще проще. Полученная допустимая область (A,B,C,D,E) показана на рис. 1.

Затем можно, определить оптимальное значение целевой функции. Построим прямую

Значение нам известно. Но можно определить тангенс угла наклона т.е. эта любая прямая В зависимости от положения прямой получаются разные значения Причем при передвижении прямой вверх и вправо значение увеличится. Прямая должна проходить через допустимую область. При этом будут получаться разрешенные значения и

Экстремальным положениям будут соответствовать точки касания прямой допустимой области: точка А соответствует минимуму , а точка D максимуму. При этом (в точке D), Это и есть максимальный доход. Задача ЛП решена.

Замечание. Решение задачи, строго говоря, не закончено, т.к. и должны быть целыми. Можно отбросить дробные значения и получить (увеличивать и нельзя, т.к. можно выйти из допустимой области). Рекомендуется округлять и до ближайшего целого. Мы получили точку F. Но можно и взять точки и , при этом Более точный алгоритм будем изучать в разделе целочисленное программирование. При этом вначале решается задача ЛП, а потом используются специальные методы для получения целочисленного решения.

Рис.1 Геометрическое решение задачи ЛП

Д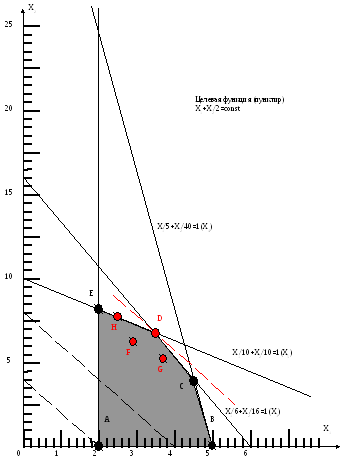опустимая область А,В,С,D,E.

Максимум целевой функции в точке D.

Целочисленное решение – точки F,G,H.

Некоторые выводы

Если в задаче ЛП существует оптимальное решение, то по крайней мере одна из вершин допустимой области представляет собой оптимальное решение.

Если прямая целевой функции совпадает с границей, то оптимальных решений будет бесконечное множество.

Позже мы введем понятие базисного решения и покажем, что им будут соответствовать точки пересечения граничных прямым. Причем среди базисных будут допустимые базисные решения (точки А…Е) и не допустимые (остальные точки пересечения прямых). Оптимальным решением является одно из допустимых базисных решений.

Отметим также, что допустимая область представляет из себя выпуклый многоугольник. Задачу можно решить и для трех переменных. Область допустимых значений будет в виде выпуклого многогранника, а целевая функция - в виде плоскости.

7