5.1. Задачи синтеза в сапр

Задача синтеза проектируемого объекта или какой-то его части сос­тоит в том, чтобы по техническому заданию или заданному функ­цио­нальному назначению объекта, или по закону его функцио­ни­рова­ния, или по промежуточным результатам получить проектное реше­ние в виде некоторого описания проектируемого объекта (или его час­ти).

Синтез нацелен на создание новых вариантов проектных реше­ний. В процессе автоматизированного проектирования объек­та ре­ша­­­­­­ется ряд задач синтеза (рис.5.1):

Рис.5.1. Задачи синтеза при автоматизированном проектировании

1. Разработка функциональной схемы. Определяются (по тех­ни­ческому заданию или аналогам) функции и задачи проектируемого объекта, а также требования к характеристикам реализации функций и задач. В зависимости от сложности объекта может быть разра­бо­та­но несколько функциональных схем (для об­ъекта в целом, для отде­ль­­ных блоков, узлов и подсистем объекта).

Примеры функций для систем автоматизированного управления: функция измерения значений параметров объекта управления; функ­ция отображения значений измеряемых параметров; функция генера­ции технологических отчётов; функция управления исполнитель­ны­ми механизмами объекта управления; функция диагностики; функция организации информационного обмена между компонентами систе­мы; функция защиты информации и т.д.

Отображение функций и задач проектируемого объекта и связей между его подсистемами приводит к получению функциональных схем этого объекта.

2. Определение состава объекта. На стадии разработки функ­цио­­­­­­нальных схем производится разбиение объекта на узлы, блоки, под­­системы и т.д. На рассматриваемом этапе уточняется разбиение объекта (машины, аппараты, системы и т.д.) на взаимосвязанные, но в определённой степени автономные узлы, блоки, подсистемы и т.д.

Затем для каждого узла, блока, подсистемы решаются задачи оп­ределения состава этих компонентов, то есть определяется какие эле­менты, комплектующие детали, устройства должны войти в состав каждого узла, блока, подсистемы объекта.

3. Структурный синтез. Структура (лат. structura) – взаимосвязь составных частей чего-либо, строение объекта.

Структурным синтезом называется проектная процедура, заклю­чающаяся в разработке или выборе структуры объекта. При струк­тур­ном синтезе определяется - как элементы, блоки, части объекта дол­жны быть связаны друг с другом. При этом САПР использует прави­ла соединения элементов, блоков, частей объекта, подсистем между собой. Результаты должны содержать состав элементов, бло­ков, уз­лов, подсистем; способы их соединения и взаимодействия.

При проектировании систем автоматического и автоматизирован­ного управления, информационно-измерительных систем, радиоэлек­тронных устройств, вычислительных систем, систем связи и электро­энергетики в результате структурного синтеза должны быть получе­ны одна или несколько (для компонентов и подсистем объекта) струк­турные схемы.

Структурная схема – схема, показывающая взаимосвязь состав­ных частей проектируемой системы. Структурная схема, какой бы сложной она ни была, состоит из четырёх типов структурных элемен­тов:

1. Структурные элементы направленного действия, называемые звеньями. Звенья несут смысловую нагрузку, определяемую особен­ностями проектируемой системы.

2. Элементов сравнения, в которых происходит сложение или вы­читание сигналов.

3. Точек разветвления или узлов, в которых путь распростране­ния сигналов разветвляется на несколько направлений, ведущих к раз­­­личным точкам системы.

4. Связей или линий структурной схемы, указывающих направле­ния передачи сигналов.

Задачи синтеза структур проектируемых объектов относятся к наи­­более трудно формализуемым. По этой причине структурный син­тез, как правило, выполняют в интерактивном режиме при решающей роли инженера-разработчика, а САПР играет вспомогательную роль: предоставление необходимых справочных данных, фиксация и оцен­ка промежуточных и окончательных результатов структурного син­те­за.

Однако имеются и примеры успешной автоматизации струк­тур­ного синтеза: автоматизированное проектирование печатных плат и кристаллов БИС, логический синтез комбинационных схем цифро­вой автоматики и вычислительной техники, синтез структур техно­ло­ги­ческих процессов и т.д.

Структурный синтез заключается в преобразовании описаний проектируемого объекта (исходное описание содержит информацию о требованиях к свойствам объекта, об условиях его функцио­ни­рова­ния, о различных ограничениях и т.д.) в результирующее опи­сание, ко­торое должно содержать сведения о структуре объекта, то есть о составе элементов и способах их соединения и взаимодействия.

4. Параметрический синтез. В процессе параметрического син­теза определяются численные значения параметров элементов, узлов, блоков, подсистем объекта. Завершающей процедурой является опре­деление значений параметров и характеристик проектируемого объ­екта в целом.

При параметрическом синтезе постоянно учитываются до­пус­тимые области значений параметров и характеристик элементов, уз­лов, блоков, подсистем и объекта в целом. Границы допустимых зна­чений (максимальные и минимальные) задаются ТЗ на проектируе­мый объект, стандартами, нормативными документами, паспортными данными используемых комплектующих деталей и компонентов, фи­зи­­ческими принципами и фундаментальными законами, положенны­ми в основу построения объекта, условиями его функционирования.

Примерами результатов параметрического синтеза могут служить диаметры труб и толщина их стенок на различных участках маги­стра­ль­­­ного газопровода или нефтепровода, параметры режимов резания в технологической операции обработки металла, параметры радиоэлек­тронных элементов устройства обработки данных и т.д.

5. Проектирование конструкции объекта. В общем виде кон­стру­ирование машин, аппаратов, устройств и других объектов пред­ставляет собой задачу геометрической компоновки заданного числа составляющих объект элементов, узлов, блоков, подсистем в задан­ном объёме либо в минимальном объёме при условии выполнения ря­да требований и ограничений.

Эта задача может быть формализована, и обобщённый компоно­вочный параметр объекта можно представить в виде:

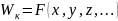, (5.1)

где x,y,z,… -составляющие обобщённого компоновочного параметра (масса, объём, стоимость, энергопотребление и т.д.).

Для количественной оценки качества конструкции проекти­руе­мо­го объекта обычно используются следующие показатели:

- плотность геометрической упаковки (компоновки);

- степень заполнения объёма;

- значение относительной массы.

Под геометрической упаковкой (компоновкой) понимают про­цесс размещения, соединения и защиты компонентов в объекте.

Плотностью (коэффициентом) упаковки К_у называют число дета­лей объекта n, размещённых в границах объёма V, то есть

(5.2)

Коэффициент заполнения объёма определяется как

(5.3)

где объём, занимаемый активными элементами, без кото­-

рых принципиально не возможно выполнение физичес­­­ко­­­­­­­­­го

проце­­сса, обеспечивающего нормальное функцио­ни­рование

про­ек­­тируемого объекта (ротор турбины, газопере­качиваю-

щий агрегат компрессорной станции магистраль­ного газо-­

провода и т.д.);

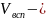объём, занимаемый вспомогательными материалами,

обес­печивающими активным элементам возможность выпол­­-

нения физического процесса (изоляционные покрытия, мон­-

тажные провода, трубопроводы и т.д.);

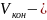объём, занимаемый конструктивными материалами,

обес­печивающими неизменность положения в пространстве

ак­тивных элементов и вспомогательных материалов для вы-

по­­л­не­ния ими физических функций (процессов), а также до-­

полнительную защиту этих элементов от внешних воздей­-

ствий (шас­­си, корпуса приборов, корпуса микросхем и т.д.).

При проектировании конструкции объекта учитываются раз­лич­ные ограничения. Это требования ТЗ, стан­дартов, технологии изго­товления узлов, блоков и других частей объекта.

Дополнительные ограничения накладываются способами и фор­мами взаимодействия проектируемого объекта с внешней средой, а также методами организации взаимодействия человека с проекти­руе­мым объектом в процессе его эксплуатации.

Задачи размещения. Одна из задач конструирования называется задачей размещения. Задача раз­­мещения весьма универсальна и ши­ро­­ко используется для ре­шения задач размещения станочного и дру­го­го производственного оборудования, энергетических узлов, узлов связи, узлов вычислительных систем, устройств автоматизированных систем управления технологическими процессами и т.д.

Задача размещения состоит в нахождении оптимального варианта расположения аппаратов, станков, агрегатов, блоков, узлов, модулей, микросхем на некоторой плоскости (площади цеха, площадки пред­прия­­тия, монтажной плате, печатной плате, карте и т.д.) в со­от­вет­ствии с критерием, который должен принять наибольшее или наи­мень­­­­­шее значение.

Математически задача размещения для электронных устройств формулируется следующим образом: задано множество N из n эле­ментов и множество связей между элементами, представленное мат­рицей | a_ij | из i строк и j столбцов.

Необходимо разместить заданное число элементов n в n под­про­странстве множества Q_n так, чтобы удовлетворить заданному крите­рию качества K. Обычно в качестве критерия качества используется один из следующих:

- критерий минимальной суммарной длины линий связи, который сводится к соотношению ;

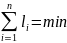- критерий ограничения максимальной длины линий связи;

- критерий минимума числа слоёв многослойной печатной платы.

Алгоритмы размещения в любой области их применения можно разделить на две группы: конструктивные, создающие размещение, и итерационные, улучшающие (оптимизирующие) начально созданное размещение.

В качестве примера рассмотрим задачу размещения на печатной плате радиоэлектронных элементов (микросхем, конденсаторов, ре­зис­­торов и т.д.).

От того, как будут размещены детали на печатной плате, зависит длина соединительных проводников, от которой, в свою очередь, за­ви­сят надёжность, уровень помех, время распространения сигналов и т.д.

Формулировка задачи размещения для рассматриваемого приме­ра: найти такое размещение компонентов d₁,d₂,…d_n на множестве по­зиций q₁,q₂,…q_m монтажного пространства, при котором суммар­ная длина электрических соеди­нений между элементами (деталями) была бы минимальной.

Математически задача размещения формулируется так: миними­зи­­ровать целевую функцию

, (5.4)

где F – критерий суммарной длины линий связи;

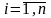
i, j – индексы детале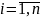й, и ;

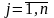n – число деталей устройства;

k, s – индексы позици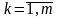й, и ;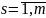

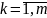m – число позиций на монтажном пространстве, m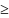 n ;

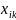и 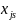- переменные;

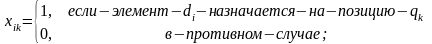
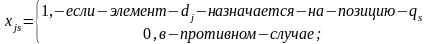
- расстояние между позициям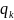и и ;

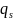P_ij – число связей (проводов, линий, цепей) между деталями d_i и d_j .

Ограничения:

- каждая деталь разместится только на одной позиции;

-на каждую позицию будет назначено не более одной детали.

Решение задачи сводится к получению

. (5.5)

Далее задача решается методами линейного прог­рамми­рова­ния.

При решении задач синтеза применяются методы оптимизации, т.е. стремятся получить оптимальную структуру объекта, оптималь­ные значения параметров и характеристик объекта, выбрать опти­мальную конструкцию аппарата, машины, агрегата и т.д.

Под оптимальным понимают такое проектное решение, которое удовлетворяет всем электрическим, экономическим и другим требо­ва­ниям ТЗ, необходимым стандартам, а критерий оптимальности, опи­­сывающий качество полученных проектных решений на данном этапе синтеза, принимает наилучшее (минимальное или максималь­ное) значение.

Кроме того, при синтезе проектируемого объекта должны быть рассмотрены следующие вопросы:

1. Вопросы взаимодействия проектируемого объекта с людьми. Должно быть обеспечено взаимодействие объекта с оператором и обслуживающим персоналом.

2. Должна быть обеспечена надёжность аппарата, механизма, машины, конструкции, системы, заданная ТЗ на проектируемый объект. При синтезе объекта должны быть предложены различные решения, обеспечивающие заданную надёжность объекта (парамет­рические методы, структурные методы и др.).

5.2. Задачи анализа в САПР. Процедуры анализа выполняются, как правило, после получения промежуточных результатов проек­ти­рования объекта, то есть эта процедура выполняется после каждого этапа синтеза (рис.5.1). В некоторых случаях анализ выпол­няется на каждом этапе синтеза по несколько раз. Кроме того, анализ выпол­ня­ется после получения окончательных результатов.

Цель анализа заключается в проверке - удовлетворяют ли полу­чен­ные проектные решения требованиям ТЗ, стандартам, фи­зи­ческим законам.

В результате выполнения процедур анализа получаем инфор­ма­цию о характере функционирования узлов, блоков, устройств, под­систем и объекта в целом, о внутренних и внешних параметрах объ­ек­­та и его подсистем.

Анализ объектов при автоматизированном проектировании ос­но­­ван на математическом моделировании, т.е. на исследовании про­ек­тируемых объектов, систем, процессов путем оперирования их мате­ма­тическими моде­лями.

Для каждого иерархического уровня объекта используются соот­ветствующие математические модели (см. лекцию 4).

В САПР в зависимости от особенностей проектируемого объекта используются процедуры одновариантного и многовариантного ана­лиза.

Одновариантный анализ означает решение соответствующих урав­нений. Поэтому методы одновариантного анализа представляют собой численные методы решения соответствующих уравнений или систем уравнений.

Многовариантный анализ заключается в многократном повторе­нии решения уравнения или систем уравнений при многократном из­менении варьируемых параметров.

В вычислительной математике известно большое количество ме­тодов численного решения уравнений и систем уравнений. Однако при­менение их в данной САПР может оказаться малоэффективным.

Поэтому при создании САПР усилия должны быть направлены не только на разработку математических моделей проектируемых объ­ектов, систем, процессов, но и на развитие численных методов ре­шения задач и алгоритмов анализа получаемых проектных реше­ний.

В САПР в большинстве случаев целесообразно включить нес­ко­ль­ко методов анализа, причём выбор того или иного метода при про­ектировании делает проектировщик.

Если в результате анализа проектного решения будут получены неудовлетворительные результаты, то САПР или проектировщик возвращают процесс проектирования на предыдущие процедуры син­теза. При проектировании сложных объектов по некоторым про­ект­ным решениям возврат на повторный синтез может происходить мно­гократно до тех пор, пока не будут получены необходимые ре­зуль­таты.

Заключение

Подробно рассмотрены задачи синтеза в САПР при ав­­­­томатизи­ро­­ванном проектировании объекта – разработка функцио­нальной схе­мы, определение состава объекта, выполнение структурного синтеза и получение структурной схемы объек­та, параметрический синтез с определением численных зна­чений па­ра­­метров элементов, узлов, блоков, подсистем объекта и характерис­тик проектируемого объ­екта в целом. При проектировании кон­­струк­ции объекта решается задача размещения - нахождение оптимального варианта расположения ап­па­ратов, станков, агрегатов, блоков, узлов, модулей, микросхем на не­­которой плоскости в со­от­вет­ствии с крите­рием, который должен принять наибольшее или наи­мень­­­шее значе­ние. Методы оптимизации обеспечивают оптимальную структуру объекта.

Процедуры анализа выполняются после каждого этапа синтеза, в ряде случаев анализ выпол­няется на каждом этапе по нес­коль­­­ко раз. Обязателен анализ окончательных результатов.

Цель анализа заключается в проверке - удовлетворяют ли полу­чен­ные проектные решения требованиям ТЗ, стандартам, фи­зи­ческим законам.

Вопросы для самопроверки

1. В какой последовательности решаются задачи синтеза при автомати­зи­рованном проектировании?

2. В чём состоит задача синтеза проектируемого объекта?

3. С какой целью при синтезе применяют методы оптимизации?

4. Расскажите о задаче размещения на печатной плате радиоэлектронных элементов.

5. С какой целью при автоматизированном проектировании выполняются процедуры анализа проектных решений?

Лекция 6. Оптимизация проектных решений

План лекции

Будут рассмотрены следующие вопросы:

- примеры оптимизационных задач и постановка задачи оптими­зации;

- критерий оптимальности;

- обзор методов оптимизации.

Литература: Л.1, Л.2, Л.3, Л.5,

6.1. Примеры оптимизационных задач и постановка задачи оптимизации

Оптимизационные задачи при автоматизированном проектиро­ва­­­нии возникают в связи с необходимостью выбора наилучших вари­ан­тов конструкции аппаратов, станков, машин, меха­низмов; парамет­ров схем и проектируемых устройств; режимов работы оборудования и т.д.

Оптимальными называются те проектные решения, которые по тем или иным соображениям предпочтительнее других.

Оптимизация проектных решений позволяет найти наилучшие геометрические, технические, экономические характеристики объекта при заданных условиях.

Максимизируемые характеристики: скорость, производитель­ность, надежность, пропускная способность, прочность (балки, фун­да­менты) и т.д.

Минимизируемые характеристики: вес (изделия), затраты на строи­­тельство или изготовление, эксплуатационные расходы, потреб­ляемая электрическая мощность, расход топлива.

Проблемы поиска оптимальных решений рассматриваются в следующих разделах математики:

• - задачи на нахождение экстремумов;

• - вариационные задачи;

• - теория игр;

• - теория графов;

• -линейное, нелинейное и динамическое программирование.

Примеры проектных оптимизационных задач.

1. Проектируется контроллер для применения в автомати­чес­ких системах управления. Возможные характеристики при реше­нии оптимизационных задач: а) надежность контроллера – должна максимизироваться; б) потребляемая мощность – должна миними­зи­роваться; в) вес (масса) контроллера – должен минимизи­ро­ваваться.

2. Проектируется магистральный нефтепровод (рис.6.1). Рас­смотрим постановку задачи в упрощенном виде.

Рис.6.1. Схема магистрального нефтепровода

Задана необходимая пропускная способность нефтепровода

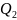/час – на участке 1 и /час – на участке 2.

Известны: длины 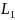км, км;

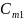С_т1, С_т2, … С_{т n} - стоимость 1 км труб различного

диа­­­­­­метра, руб./км (включая затраты на прокладку);

С_ДНС - затраты на сооружение одной дожимной

насос­ной станции.

Необходимо определить число дожимных насосных станций, мес­та их размещения и диаметр труб. При увеличении числа ДНС диа­метр труб может быть уменьшен.

Необходимо минимизировать затраты на строительство магис­трального нефтепровода, т.е. С  min.

Если учитывать не только капитальные затраты, но и эксплуата­ционные (электроэнергия на питание электродвигателей, отопление зданий ДНС, зарплата персонала и др.) задача усложняется.

3. Проектируется магистральный газопровод (рис.6.2):

Рис.6.2. Схема магистрального газопровода

Рассмотрим постановку задачи в упрощенном виде.

Задана необходимая пропускная способность газопровода:

/час - на участке 1 и /час – на участке 2.

Известны: длины км и км; С_т1, С_т2, … С_{т n} - стоимость 1 км труб различного диаметра, руб./км (включая затраты на прокладку);

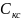- затраты на сооружение одной компрессорной станции.

Необходимо определить число компрессорных станций, места их размещения и диаметр труб на различных участках.

Если учитывать не только капитальные затраты, но и эксплу­атационные (топливо на газотурбинные установки, отопление зданий КС, зарплата персонала и др.), задача усложняется.

4. Проектируется высоковольтная ЛЭП (35, 110, 220 кВ и т.д.).

Сооружение каждой опоры связано с расходами (металлокон­ст­рукции, фундамент, монтажные работы и т.д.). Поэтому стремятся к уменьшению количества опор на трассе ЛЭП. Однако большие рас­стояние между опорами приводят к большому провисанию проводов, к необходимости применения более прочных изоляторов. Возникает необходимость применения проводов большего диаметра, т.е. возрас­тают расходы на приобретение проводов. При проектировании необ­ходимо учитывать величину силы тока в ЛЭП, климатические усло­вия, число проводов ЛЭП и т.д.

Математические модели оптимизируемых объектов можно харак­теризовать конечной совокупностью числовых параметров, которые можно разделить на три группы:

- внутренние;

- внешние;

- выходные.

Под внутренними параметрами понимаются параметры отдель­ных элементов, составляющих оптимизируемый объект. Так, при про­­­­­ек­тировании электронного устройства внутренними параметрами являются электрические параметры сопротивлений, ёмкостей, индук­тивностей, токов, напряжений и др. При проектировании интеграль­ных микросхем внутренними параметрами являются не только элек­трические, но также геометрические и физико-структурные парамет­ры.

Внешние параметры характеризуют влияние внешней среды на оптимизируемый объект. Примеры: параметры входных сигналов, тем­пература окружающей среды, механические воздействия, шумо­вые воздействия среды на объект и т.д.

Выходные параметры отражают свойства и характеристики оп­ти­­­мизируемого объекта. Примеры: потребляемая мощность, быс­тро­дей­ствие, скорость движения, габариты, стоимость и т.д.

Введём следующие обозначения.

Вектор внутренних параметров: или 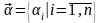. (6.1)

Вектор внешних параметров:

или 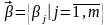. (6.2)

Вектор выходных параметров:

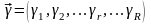или 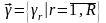. (6.3)

Компоненты векторов и являются независимыми перемен­ными, определяющими значения выходных параметров.

Таким образом, существует функциональная связь

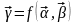. (6.4)

Только часть внутренних параметров может изменяться в про­цес­се оптимизации. Изменяемые внутренние параметры называют уп­рав­­­ляемыми параметрами или параметрами оптимизации. Эти пара­метры образуют вектор, являющийся подвектором вектора :

или 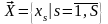. (6.5)

Следовательно, .

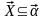Введём обозначения для тех внутренних параметров, значения ко­­торых не могут изменяться в процессе оптимизации. Эти парамет­ры представляют собой вектор

или . (6.6)

Естественно, что 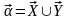. (6.7)

Для того, чтобы судить о качестве проектных решений и срав­нивать получаемые решения между собой, нужно иметь некоторый численный критерий оптимальности (показатель оптимальности ре­­ше­­ния) – W.

Конкретный вид критерия W зависит от проектируемого объек­та, от этапа проектирования, от того, какая часть объекта проек­тируется. Простейшая оптимизационная задача – это определение экс­тремума функции одной переменной величины (рис.6.3).

Рис.6.3. Экстремум функции

Решение опирается на теорему Ферма: Если функция W = f(z), имеющая производную, при 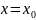z=z₀ принимает минимум или максимум, то производная от этой функции при z=z₀ обращается в ноль.

При разработке САПР объектов определённого класса должна быть найдена зависимость

, (6.8)

где 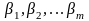- внешние параметры;

- внутренние параметры, которые не могут быть изменены;

- элементы решения оптимизационной задачи (результаты решения).

Выражение (6.8) означает, что при заданных значениях парамет­ров ; необходимо найти такие значения элементов решения , которые в зависимости от характера критерия W обращали бы его в максимум или в минимум, то есть

W  max или W min .

Как правило, оптимизационные задачи решаются с учётом ограничений двух видов: функциональных и критериальных.

Функциональные ограничения включают в себя условия работо­способности объекта, имеющие принципиальное значение при оценке правильности его функционирования. Эти ограничения задаются в виде системы равенств и неравенств:

x_s  a_s ; x_q  a_q ; x_d = a_d , (6.9)

где a_s, a_q, a_d – заданные числовые значения выходных парамет­ров,

; ; .

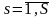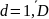Примеры функционального ограничения: коэффициент обратной связи в схеме генератора должен быть больше некоторого крити­чес­кого значения, порог срабатывания ждущей релаксационной схемы должен находиться в заданных пределах и т.д.

Вторая группа ограничений называется критериальными ограни­чениями :

x_s  a_s ; x_q  a_q ; x_d = a_d , (6.10)

где a_s, a_q , a_d - заданные числовые значения выходных параметров, .

Примеры критериальных ограничений: ограничения на стои­мость объекта, на быстродействие, время срабатывания, габариты объ­екта и т.д.

Функциональные и критериальные ограничения образуют основную часть требований к проектируемому объекту. Кроме того, должны учитываться ограничения на допустимые диапазоны изменения значений компонент внешних параметров:

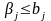; , (6.11)

где b_j – заданные значения внешних параметров, .

6.2. Критерий оптимальности

Качество проектируемого объекта характеризуется некоторым числовым показателем W, который в результате процедур оптими­зации требуется обратить в экстремум – в максимум, а в неко­торых случаях – в минимум.

В процессе оптимизации по выбранному или заданному (нап­ример, техническим заданием) критерию оптимальности в соот­вет­ствии с принятым методом оптимизации находятся проектные реше­ния, которые должны привести к получению максимального или (в не­которых случаях) минимального значения критерия W.

Однако во многих случаях проектируемый объект характе­ри­зуется несколькими показателями качества.

Пусть задан ряд показателей качества проектируемого объекта w_i, , где, например, w₁- стоимость разработки, w₂ –коли­че­ствен­ная ха­рак­теристика надёжности, w₃ – потребляемая мощность; w₄ – мас­са объекта и т. д.

Совокупность этих показателей даёт полное представление о том, насколько полученные проектные решения удовлетворяют техничес­кому заданию на разработку.

Оптимизационные задачи с несколькими критериями называются многокритериальными.

При нескольких критериях оптимальности w₁,w₂,…,w_i,…,w_n мо­гут использоваться различные методы решения поставленной задачи.

Один из методов состоит в том, что из всех частных критериев w_i выбирается один. Выбор этого критерия осуществляется или методом экспертных оценок, или он назначается заказчиком проектной или конструкторской работы.

Предположим, выбран критерий w₂. Обозначим выбранный кри­те­рий как w_гк =w₂ (индекс ГК – главный критерий). При проек­ти­ро­вании или конструировании стремятся максимизировать или мини­ми­зи­ровать (в зависимости от того, какая характеристика объекта вы­бра­­на для оптимизации) значение критерия w_гк. На все остальные кри­­те­рии накладываются ограничения вида

w₁ A; w₃ B и т.д. (6.12)

Предположим, проектируется электронное устройство и в ка­че­стве w_гк выбрана надёжность. При этом быстродействие w₁ не должно быть меньше А, а стоимость w₃ не должна превышать неко­торого зна­че­ния В.

Другой подход состоит в том, что осуществляют объединение различных критериев в один многокомпонентный. Могут исполь­зо­ваться различные способы такого объединения.

1. Строится обобщённый критерий в аддитивной форме

, (6.13)

где w_i – i-ый частный критерий;

a_i – весовой коэффициент i-го частного критерия;

n – количество критериев.

При этом a_i0 при тех показателях, которые надо максими­зи­ро­вать, и a_i0 при тех показателях, которые необходимо минимизи­ро­вать.

Абсолютные значения весовых коэффициентов a_i соответствуют степени важности соответствующих критериев. Для получения значе­ний весовых коэффициентов используют методы экспертных оценок. Может быть использован метод ранжирования.

В (6.13) все слагаемые должны быть в безразмерной форме, так как нельзя суммировать рубли, тонны, м³ и т.д. Поэтому норми­рую­щие коэффициенты a_i должны иметь такую размерность, что­бы пре­об­разовать соответствующее слагаемое в (6.13) в без­раз­мерную фор­му. Предположим, критерий w₂ имеет размерность |кг|. Тогда коэф­фи­циент a_i должен иметь размерность 1/кг.

В некоторых случаях более целесообразным является опериро­ва­ние не с абсолютными, а с относительными изменениями значений част­­ных критериев. В этом случае применяют мультипли­кативный критерий оптимальности

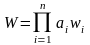. (6.14)

6.2. Обзор методов оптимизации

В процессе автоматизированного проектирования, например, не­ко­торого объекта, требуется определить его параметры таким образом, чтобы максимизировать надёжность, быстродействие, скорость, точность, производительность и др., мини­ми­зировать стои­мость, габариты, массу и др. Решение задачи обеспе­чивается варьи­рованием параметров Х в некоторой допустимой обла­сти D, которая формируется системой ограничений типа равенств и нера­венств и определяется требованиями технологии.

Основными методами оптимизации в САПР являются поисковые методы, которые основаны на пошаговом изменении тех параметров, которые могут быть изменены в процессе выполнения проектных про­­це­­дур, т.е.

, (6.15)

где приращение ΔХ_k вектора варьируемых параметров вычисляется по формуле

. (6.16)

Здесь X_k – значение вектора варьируемых параметров на k-м ша­ге; h – номер шага; g(X_k) – направление поиска. Если выполняется условие сходимости, то реализуется пошаговое (итерационное) при­бли­жение к экстремуму.

Методы оптимизации классифицируются по ряду признаков. В зависимости от числа критериев оптимальности различают методы од­­но­­мерной и многомерной оптимизации. В первых из них критерий – единственный, во вторых – размер вектора W не менее двух. Реаль­ные задачи в САПР – многомерны, методы одномерной оптими­зации играют вспомогательную роль на отдельных этапах многомер­ного поиска.

Различают методы условной (имеются ограничения) и бе­зус­лов­ной (отсутствие ограничений) оптимизации. Для реальных задач характерно наличие ограничений, однако методы безусловной опти­мизации также представляют интерес, поскольку задачи услов­ной оп­тимизации с помощью специальных методов могут быть сведе­ны к задачам без ограничений.

Методы решения оптимизационных проектных задач, в которых критерий оптимизации является функцией n переменных, называют методами математического программирования. (Термин «программи­ро­ва­ние» в данном случае обусловлен тем, что в задачах ищется неко­то­рая программа действий).

В математическом программировании выделяют следующие разделы:

- линейное программирование;

- нелинейное программирование;

- динамическое программирование.

Для случаев, когда критерий W зависит от элементов решения x₁,x₂,…,x_n линейно, и ограничения, наложенные на x₁,x₂,…,x_n, также имеют вид линейных равенств (или неравенств), максимум (или ми­ни­мум), функция W находится с помощью математических методов линейного программирования.

Задачу линейного программирования можно записать следую­щим образом:

найти x_j0 (j=1,2,…,n) при ограничениях типа

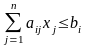, (i=1,2,…,m₁) ;

, (i=m₁₊₁, m₁₊₂,…,m₂) ; (6.17)

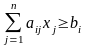, (i=m₂₊₁,m₂₊₂,…, m) ,

которые минимизируют (или максимизируют) линейную функ­цию

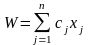. (6.18)

В (6.17) и (6.18) - это параметры проектируемого или конструируемого объекта.

Для решения задач линейного программирования разработаны как методы решения, так и вычислительные алгоритмы (алгоритмы симплексного метода, целочисленного программирования и др.). Ограничения могут отсутствовать. В этом случае мы имеем задачу безусловной оптимизации.

Итак, задача линейного программирования состоит в миними­за­ции или максимизации линейной функции при линейных ограниче­ниях. Однако во многих оптимизационных задачах автоматизи­рованного проектирования целевая функция или функции, задающие ограничения, не являются линейными. Такие задачи называются задачами нелинейного программирования.

Оптимизационная задача нелинейного программирования – это задача максимизации или минимизации целевой функции (критерия оптимизации)

(6.19)

при условиях ;

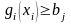; (6.20)

.

В (6.19) и (6.20) 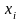- это параметры проектируемого или конструируемого объекта. Условия (6.20) являются ограничениями за­­дачи. Ограничения могут отсутствовать. В этом случае мы имеем задачу безусловной оптимизации.

Для решения задач нелинейного программирования применяется несколько методов.

Основная идея градиентного метода состоит в замене максими­зируемой (минимизируемой) функции в окрестности конкретной точки её линейным приближением.

Как и в случае задач линейного программирования, для задач не­ли­нейного программирования, содержащих только две перемен­ные, возможна графическая интерпретация, то есть может исполь­зоваться графический метод решения задач нелинейного программирования.

Метод множителей Лагранжа основан на том, что линия уровня целевой функции с максимальным значением будет касаться линии границы в точке, являющейся оптимальным решением задачи.

Динамическое программирование представляет собой метод оп­ти­мизации решений, специально приспособленный к многоша­го­вым или многоэтапным операциям.

Поставим задачу динамического программирования в общем виде. Пусть имеется операция Q с аддитивным критерием оптималь­ности, распадающаяся (естественно или искусственно) на m шагов. На каждом шаге принимается какое-то решение w_i. Требуется найти оптимальное решение

W=(w₁,w₂,…,w_m) ,

при котором критерий оптимальности (показатель эффективности)

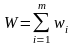
обращается в максимум.

Поставленную задачу можно решать по-разному: или искать сра­зу оптимальное решение W, или же находить его постепенно, шаг за шагом, на каждом этапе расчёта оптимизируя только один шаг.

Такая идея постепенной, пошаговой оптимизации и составляет суть метода динамического программирования.

Планируя многошаговую операцию, необходимо выбирать реше­ние на каждом шаге с учётом его будущих последствий на ещё пред­стоящих шагах.

Процесс динамического программирования разворачивается от конца к началу: раньше всех планируется m-ый шаг. Для этого нужно сделать разные предположения о том, чем закончился предпоследний (m-1)-й шаг, и для каждого из них найти такое решение, при котором результат на последнем шаге был бы максимален. Решив эту задачу, мы найдём условное максимальное решение на m-ом шаге, то есть то решение, которое надо принять, если (m-1)-й шаг закончился определённым образом.

Предположим, что эта процедура выполнена и для каждого исхо­да (m-1)-го шага. Теперь мы можем оптимизировать решения на пред­последнем (m-1) шаге. Сделаем все возможные предположения о том, чем может закончиться (m-2)-й шаг, и для каждого из этих пред­по­ло­жений найдем такое решение на (m-1)-м шаге, чтобы вы­игрыш за два последних шага (из которых последний уже оптими­зи­ро­ван) был мак­симизирован. Далее оптимизируется решение на (m-2)-м шаге и т. д.

Теперь предположим, что условное оптимальное решение на каж­дом шаге нам известно: мы знаем, что делать дальше, в каком бы сос­тоянии ни был процесс к началу следующего шага. Тогда мы мо­жем найти уже не «условное», а просто оптимальное решение на каждом шаге.

Действительно, пусть нам известно начальное состояние процесса, обозначим его S₀. На первом шаге надо применить усло­в­ное оптимальное решение, выработанное для первого шага, относя­щееся к состоянию S₀. В результате этого решения после первого ша­га система перейдёт в другое состояние S₁, но для этого состояния мы снова знаем условное оптимальное решение на втором шаге w₂ и так да­лее. Таким образом, будет найдено оптимальное решение 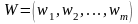, приводящее к максимально возможному значению критерия W_max.

Таким образом, при оптимизации методом динамического программирования многошаговый процесс проходится дважды:

- первый раз – от конца к началу, в результате чего находятся условные оптимальные решения на каждом шаге и оптимальный выигрыш (тоже условный) на всех шагах, начиная с данного и до конца процесса;

- второй раз – от начала к концу, в результате чего находятся (уже не условные) оптимальные решения на всех шагах вычис­ли­тельного процесса.

Заключение

Оптимизационные задачи при автоматизированном проекти­ро­­ва­­­нии возникают в связи с необходимостью выбора наилучших ва­ри­ан­тов построения объекта. Внут­ренние, внешние и выходные пара­мет­­­­ры определяют оптимизи­руе­мый объект. Только часть внутрен­них параметров может изменяться в про­цес­се оптимизации. Изменяе­мые внутренние параметры называ­ют уп­рав­­­ляемыми параметрами или параметрами оптимизации. Зада­ча состоит в том, что при задан­ных значениях внешних парамет­ров необходимо найти такие значения элементов реше­ния , которые в зависимости от характера критерия W обращали бы его в максимум или в минимум. При этом необходим учёт функциональных и крите­ри­­альных ограничений.

Основными методами оптимизации в САПР являются поисковые методы, которые основаны на пошаговом изменении тех параметров, которые могут быть изменены в процессе выполнения проектных про­­­це­­дур. Реаль­ные задачи в САПР требуют многомерной оптимиза­ции, и решаются методами математического программирования.

Вопросы для самоконтроля

1. С какой целью при автоматизированном проектировании применяются методы оптимизации?

2. Назовите некоторые максимизируемые и минимизируемые характе­рис­тики проектируемых объектов?

3. Приведите примеры проектных оптимизационных задач?

4. В моделях оптимизируемых объектов какие параметры являются внут­ренними, внешними и выходными?

5. Какие параметры называют параметрами оптимизации?

6. Что собой представляет критерий оптимальности?

7. С какой целью в оптимизационных задачах используются ограничения?

8. Какие задачи оптимизации называются однокритериальными?

9. Какие задачи оптимизации называются многокритериальными?

10. Как на базе частных критериев осуществляется создание обобщённых критериев оптимальности?

11. Как формулируется задача линейного программирования?

12. Как формулируется задача нелинейного программирования?

13. Как формулируется задача динамического программирования?

Лекция 7. Математическое обеспечение синтеза и анализа проектных решений

План лекции

Будут рассмотрены следующие вопросы:

- математическое обеспечение синтеза проектных решений;

- математическое обеспечение анализа проектных решений.

Литература: Л.3, Л.4, Л.5.

7.1. Математическое обеспечение синтеза проектных решений

Задача синтеза проектных решений состоит в таком выборе струк­­туры проектируемого объекта, его параметров, характеристик и технических средств реализации, чтобы удовлетворить совокупности требований, заданных техническим заданием на проектирование.

Очевидно, что сформулировать единый критерий оптимальности проектируемого объекта и решить задачу синтеза как задачу синтеза по этому критерию в большинстве случаев не представляется воз­мож­ным. Поэтому общая задача синтеза объекта обычно разбивается на ряд подзадач:

- разработка функциональной схемы;

- определение структуры объекта;

- определение параметров объекта;

- выбор элементов (комплектующих деталей);

- конструирование аппаратуры.

Кроме того, для объектов, в состав которых входят компью­тер­ные средства, одна из задач синтеза состоит в выборе и разработке программного обеспечения.

Структурный синтез

Разработка или выбор структуры объекта есть проектная про­це­дура, называемая структурным синтезом.

Задачи структурного синтеза, как правило, являются многокри­териальными (см. лекцию 6).

В качестве примера укажем, какие сведения должны быть вклю­чены в качестве исходных данных в задачу синтеза структуры авто­ма­тизированной системы управления:

- перечень выполняемых системой функций;

- типы допустимых для использования аппаратно-программных средств, выполняющих функции системы;

- множество внешних источников и потребителей информации;

- различного рода ограничения, в частности ограничения на затраты материальных ресурсов и на затраты времени на выполнение функций системы.

В некоторых случаях может быть задана исходная структура сис­темы в виде взаимосвязанной совокупности аппаратно-программных средств. Эта структура может рассматриваться как обобщённая избы­точная или как вариант первого приближения.

Конструирование, разработка технологических процессов, офор­мление технической документации – частные случаи струк­турного синтеза.

В САПР применяют как средства формального синтеза проект­ных решений, выполняемого в автоматическом режиме, так и вспо­могательные средства, способствующие выполнению синтеза про­­ект­ных решений в интерактивном режиме. К вспомогательным сред­ствам относятся базы данных по типовым проектным решениям, системы обу­че­ния проектированию и др.

Задачи синтеза структуры объектов относятся к наиболее трудно формализуемым. По этой причине структурный синтез, как правило, вы­полняют в интерактивном режиме при решающей роли проек­ти­ров­щика, а ЭВМ играет вспомогательную роль: предоставление необ­ходимых справочных данных, оценка промежуточных и оконча­тельных результатов.

Однако имеются примеры успешной автоматизации структурного синтеза: проектирование печатных плат, интегральных микросхем, синтеза технологических процессов и т.д.

Структурный синтез заключается в преобразовании исходного описания объекта, содержащего информацию о требованиях к свой­ствам объекта, об условиях его функционирования, в резуль­тирую­щее описание, содержащее сведения о структуре объекта, т.е. о сос­таве элементов, способах их соединения и взаимодействия.

Задачу принятия проектных решений в процессе структурного син­теза формулируют следующим образом:

ЗПР = < А, К, Мод, Р > , (7.1)

где: А – множество альтернатив проектного решения;

К=(k₁, k₂,…,k_m) – множество критериев (выходных парамет­ров), по которым оценивается соответствие альтернативы поставлен­ным це­лям;

Мод – математическая модель, позволяющая для каждой аль­тер­нати­вы рассчитать значения критериев К= ;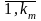

Р – решающее правило для выбора наиболее подходящей аль­терна­тивы проектного решения.

Каждой альтернативе можно поставить в соответствие значения упорядоченного множества (набора) атрибутов Х=<х₁,х₂,…,х_n> , ха­рак­тери­зую­­щих свойства альтернативы.

Модель Мод называют структурно-альтернативной, если среди имеются параметры, характеризующие структуру проек­ти­руе­мого объекта.

В большинстве случаев структурного синтеза математическая мо­дель в виде алгоритма, позволяющего по заданному множеству Х и намеченной структуре объекта рассчитать вектор критериев К, ока­зывается известной.

Однако в ряде других случаев модели не известны в силу недос­та­точной изученности процессов и объектов, но известна совокуп­ность наблюдений над объектами данного класса. Тогда для полу­че­ния моделей используются методы идентификации и эксперимен­тальных исследований.

В связи с изложенным, большинство задач структурного синтеза решают с помощью приближённых методов. Эти методы не гаран­ти­руют получение оптимального решения, но приводят к резуль­татам, близким к оптимальным.

Простейший способ задания множества А – перечисление всех аль­тер­натив. Описание альтернатив может храниться в базе данных САПР.

Кроме того, может использоваться неявное описание А в виде ал­го­­­ритма и набора правил Р синтеза структуры из набора элементов Э. Поэтому здесь

А=< P,Э > , (7.2)

а процесс синтеза структуры объекта состоит из следующих этапов:

- формирование альтернативы A_j – это может быть выбор из ба­зы данных САПР или генерация структуры из Э в соответствии с пра­вилами P;

- оценка альтернативы по результатам моделирования с помо­щью модели Мод;

- принятие решения относительно перехода к следующей аль­тер­нативе или прекращение процесса синтеза (решение принимается про­­­­ек­тировщиком или системой автоматизированного проек­тиро­вания).

Для описания множества Р (набора правил синтеза структуры объекта) и Э (набора элементов, которые могут использоваться для синтеза структуры объекта) используют следующие подходы:

- морфологические таблицы и альтернативные И-ИЛИ-деревья;

- представления знаний в интеллектуальных системах;

- базы данных с информацией об аналогах объектов данного ти­па.

Морфологическая таблица (М) представляет собой обобщённую структуру в виде множества функций, выполняемых компонентами синтезируемых объектов рассматриваемого класса, и подмножество способов их реализации. Каждой функции можно поставить в соответствие одну строку таблицы, каждому способу её реализации – одну клетку в этой строке.

На базе М возможно построение методов синтеза с элементами алгорит­мизации.

Л юбую морфологическую таблицу можно представить в виде дерева (рис.7.1). На рисунке функции показаны рёбрами, идущими вниз из вершины М (вершина И); значения функций – множество рёбер, идущих вниз из вершин ИЛИ (светлые кружки). Алгорит­мизация синтеза на базе И-ИЛИ – деревьев требует введения правил выбора альтернатив в каждой вершине. Эти правила связаны с тре­бованиями ТЗ и должны отражать запреты на сочетания опреде­лён­ных компонентов структур.

Рис.7.1.Дерево, соответствую­-

щее морфологической таблице

Вторая проблема после фор­мализации задачи синтеза структуры проекти­руемого объ­­екта - это выбор метода решения.

Если при формализации задачи синтеза удалось все проектные па­раметры представить в числовом виде, то можно применить рас­смотренные выше методы математического программирования.

Однако применение точных методов математического прог­рам­мирования при синтезе структуры объекта сопряжено с большими труд­ностями. Поэтому при синтезе структуры объекта лидирующее положение занимают приближённые методы. Широко применяются операции разделения множества вариантов на подмножества и отсе­че­ние неперспективных подмножеств. Эти методы объединяются под названием метода ветвей и границ.

В системах автоматизированного проектирования расширяется при­­менение интеллектуальных систем. При этом структурный синтез реализуется с помощью экспертных систем

ЭС = < БД, БЗ, И > , (7.3)

где: БД – база данных САПР, включающая сведения об элементах, которые мо­­гут использоваться в проектируемом объекте;

БЗ – база знаний, содержащая правила проектирования вариантов структуры объекта;

И – интерпретатор, устанавливающий последовательность применения правил из базы знаний.

Параметрический синтез. Цель параметрического синтеза зак­лю­чается в задании или расчёте значений параметров проектируе­мо­го объекта. Примерами результатов параметрического синтеза могут служить геометрические размеры детали в механическом узле, пара­метры электрорадиоэлементов в электронном устройстве, значения давления и температуры в аппарате для обработки нефти, параметры режимов резания в технологической операции и т.д.

Задача параметрического синтеза может быть сформулирована как задача определения значений параметров элементов, наилучших с позиций удовлетворения требований технического задания при неиз­менной структуре проектируемого объекта.

Наиболее распространённой является детерминированная поста­новка задачи параметрического синтеза: заданы условия работоспо­собности на выходные параметры Y, и нужно найти номинальные зна­­чения проектных параметров Х, к которым относятся параметры всех или части элементов проектируемого объекта. Эту задачу назы­вают базовой.

Базовая задача параметрической оптимизации ставится как зада­ча математического программирования (см. лекцию 6). Для осуще­ствления базовой задачи параметрической оптимиза­ции необходимо выбрать критерий оптимальности (см. лекцию 6), затем разработать целевую функцию и определить систему ограниче­ний. Затем должна быть решена задача поиска экстремума целевой функции (см. лекцию 6).

7.2. Математическое обеспечение анализа проектных решений

Цель анализа – получение информации о характере функциони­ро­­­вания объекта, о значениях выходных параметров при синтезиро­ванной структуре объекта, сведения о значениях параметров элемен­тов объекта.

К математическому обеспечению анализа относятся математичес­кие модели анализа проектных решений, численные методы и алго­рит­мы выполнения проектных процедур анализа.

Вычислительный процесс при анализе проектных решений состо­ит из этапов формирования математической модели и её исследова­ния (решения). На рис.7.2 показаны основные этапы разработки ма­те­матичес­кой модели анализа проектных решений.

Рис.7.2. Этапы разработки математической модели

анализа проектных решений

Системы автоматизированного проектирования осуществляют ана­лиз проектных решений на микроуровне, макроуровне, функ­цио­нально-логическом уровне и на системном уровне. При этом на этих иерархических уровнях проектирования для построения матема­тических моделей анализа проектных решений используется различ­ный математический аппарат.

Математические модели анализа проектных решений на микроуровне. Математическими моделями на микроуровне явля­ют­ся как обыкновенные дифференциальные уравнения, так и диффе­рен­циальные уравнения в частных производных.

Объектами анализа проектных решений на микроуровне явля­ются строительные конструкции, детали машин, механизмов, аппара­тов, жидкие среды, электронные приборы и т.д.

Характерными примерами математических моделей микроуровня могут служить уравнения математической физики вместе с задан­ными краевыми условиями.

В САПР решение дифференциальных и интегро-диффе­рен­циаль­ных уравнений выполняется численными методами. Эти методы основаны на дискретизации независимых переменных – их пред­став­ле­нии конечным множеством значений в выбранных узловых точках исследуемого пространства. Эти точки рассматриваются как узлы не­ко­торой сетки. Поэтому используемые в САПР на микроуровне методы – это сеточные методы.

Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей (МКР) и метод конечных элементов (МКЭ).

В методе конечных разностей алгебраизация производных по пространственным координатам базируется на аппроксимации произ­водных конечно-разностными выражениями. При использовании ме­то­­да нужно выбирать шаги сетки по каждой координате и вид шаб­лона. Под шаблоном понимают множество узловых точек, значения переменных в которых используются для аппроксимации производ­ной в одной конкретной точке.

Метод конечных элементов основан на аппроксимации не произ­водных, а самого решения V(z). Но поскольку оно неизвестно, то ап­проксимация выполняется выражениями с неопределёнными коэф­фициентами q_i

, (7.4)

где - вектор-строка неопределённых коэффициентов;

- вектор-столбец координатных (иначе опорных) функций, заданных так, что удовлетворяются граничные условия.

Математические модели анализа проектных решений на макро­уровне. Для математического описания проектируемых объ­ек­тов на макроуровне используются системы обыкновенных диффе­рен­циальных и алгебраических уравнений. Аналитические решения та­ких систем получить не удаётся, поэтому в САПР преиму­ще­ственно используются алгоритмические модели.

Исходными для формирования математических моделей об­ъ­ектов на макроуровне являются компонентные и топологические уравнения.

Компонентными уравнениями называют уравнения, описываю­щие свойства элементов (компонентов), другими словами – это урав­не­ния математических моделей элементов (ММЭ).

Топологические уравнения описывают взаимосвязи элементов (компонентов) в составе проектируемого объекта.

В совокупности компонентные и топологические уравнения проектируемого объекта представляют собой математическую модель для анализа проектных решений.

Компонентные и топологические уравнения для объектов раз­лич­ной физической природы отражают разные физические свой­ства, но могут иметь одинаковый формальный вид.

Одинаковая форма записи математических соотношений позво­ля­ет говорить о формальных аналогиях компонентных и топологи­ческих уравнений. Такие аналогии существуют для механических, электрических, гидравлических, пневматических, тепловых объектов.

Наличие аналогий означает, что значительная часть алгоритмов формирования моделей анализа на макроуровне оказывается инвари­антной и может быть применена к анализу проектных решений объектов различного вида.

Единство математического аппарата формирования математи­чес­ких моделей анализа на макроуровне особенно удобно при анализе объектов, состоящих из физически разнородных подсистем.

В общем виде компонентные уравнения имеют вид:

, (7.5)

топологические уравнения

, (7.6)

где V=(v₁,v₂,…,v_n) – вектор фазовых переменных;

t- время.

Различают фазовые переменные двух типов – фазовые пере­мен­ные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток).

Каждое компонентное уравнение характеризует связь между раз­­­нотипными фазовыми переменными, относящимися к одному ком­поненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение – связи между однотипными фазовыми переменными в разных компонентах.

При разработке математических моделей анализа на макро­уров­не можно вначале использовать и графические формы представ­ления моделей.

Анализ процессов в проектируемых объектах можно проводить во времени и в частотной области. Анализ во временной области (динамический анализ) позволяет получить картину переходных процессов, оценить динамические свойства объекта. Анализ в час­тот­ной области применяют при анализе устойчивости, оценке искажений информации и т.д.

Методы анализа во временной области – это численные методы интегрирования систем обыкновенных дифференциальных уравнений

. (7.7)

Другими словами, это методы алгебраизации дифференциаль­ных уравнений. Формулы интегрирования систем обыкновенных диф­­ференциальных уравнений могут входить в математическую мо­дель независимо от компонентных уравнений или быть интегри­ро­ван­ными в математические модели компонентов.

Применяют два типа методов интегрирования – явные (экстраполяционные или методы, основанные на формулах интегрирования вперёд) и неявные (интерполяционные, основанные на формулах интегрирования назад).

Одновариантный анализ позволяет получить информацию о состоянии и поведении проектируемого объекта в одной точке прос­транства внутренних Х и внешних Q параметров. Однако для оценки свойств проектируемого объекта этого недостаточно. Нужно выпол­нять многовариантный анализ, то есть исследовать поведение объекта в ряде точек анализируемого пространства, которое можно называть пространством аргументов.

Чаще всего многовариантный анализ в САПР осуществляется в интерактивном режиме, когда проектировщик неоднократно меняет в математической модели те или иные параметры из множеств X и Q, выполняет одновариантный анализ и фиксирует полученные значе­ния выходных параметров.

Подобный многовариантный анализ позволяет оценить степень выполнения ТЗ на проектирование, разумность принимаемых проме­жу­­точных проектных решений.

Математические модели анализа проектных решений на функционально-логическом уровне. На функционально-логичес­ком уровне осуществляют анализ проектных решений достаточно слож­­ных узлов и блоков, считающихся объектами и системами на макроуровне.

Для упрощения вместо двух типов фазовых переменных моде­лей макроуровня в моделях функционально-логического уровня фи­гу­­­рируют переменные одного типа, называемые сигналами. Физи­чес­кий смысл сигнала, то есть его отнесение к фазовым переменным, кон­кретизируют в каждом конкретном случая, исходя из особен­нос­тей задачи.

Основой моделирования аналоговых устройств на функцио­наль­но-логическом уровне является использование аппарата передаточ­ных функций. При этом математическую модель каждого элемента представляют в виде уравнения

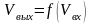, (7.8)

где сигналы на выходе и входе каждого элемента соот­ветственно.

Если элемент имеет несколько входов и один выход, то в (7.8) скаляры становятся векторами.

Для получения (7.8) в общем случае требуется предварительная алгебраизация математической модели. Такую алгебраизацию выпол­няют, например, с помощью преобразования Лапласа, переходя из временной области в пространство комплексной переменной p.

Математические модели блоков и устройств представляют моде­ля­ми типовых блоков (звеньев) из числа заранее разработанных и хранящихся в библиотеке моделей САПР.

Обычно модели звеньев имеют вид

, (7.9)

где - передаточная функция звена.

В результате на функционально-логическом уровне получаем ма­те­ма­тическую модель системы (ММС) в виде совокупности мате­ма­тических моделей элементов (ММЭ). ММС будет представлять собой систему алгебраических уравнений.

Итак, анализ проектных решений на функционально-логическом уровне сводится к следующим операциям:

1) проектируемое устройство представляют совокупностью звень­­­ев, но если это полностью или частично сделать не удаётся, то разрабатывают оригинальные модели;

2) формируют математическую модель системы (устройства) из мо­делей звеньев;

3) применяют прямое преобразование Лапласа к входным сиг­налам;

4) решают систему уравнений математической модели системы (устройства);

5) с помощью обратного преобразования Лапласа возвращаются во временную область из области комплексной переменной p.

Анализ дискретных устройств на функционально-логическом уро­в­­­­не требуется, прежде всего, при автоматизированном проекти­ровании электронных устройств, устройств цифровой автоматики и вы­числительной техники. Здесь дополнительно к допущениям, при­ни­маемым при анализе аналоговых устройств, используют дискре­тизацию сигналов, причём базовым является двузначное представ­ление сигналов. Тогда для моделирования можно использовать аппа­рат математической логики.

Элементами цифровых устройств на функционально-логическом уровне являются элементы, выполняющие логические функции и функции хранения информации.

Различают синхронные и асинхронные модели.

Синхронная модель – представляет собой систему логических уравнений, но в ней отсутствует такая переменная, как время. Син­хрон­ные модели применяют для анализа установившихся состояний. Методы анализа синхронных моделей представляют со­бой методы ре­ше­ния систем логических уравнений. К этим методам относят ме­тод простых итераций и метод Зейделя, которые анало­гич­ны одно­имён­­ным методам решения систем алгебраических уравне­ний в не­пре­рывной математике.

Согласно методу простых итераций, в правые части уравнений мо­­де­ли на каждой итерации подставляют значения переменных, по­лу­­ченные на предыдущей итерации.

В отличие от этого в методе Зейделя, если у некоторой пере­менной обновлено значение на текущей итерации, именно его и ис­пользуют в дальнейших вычислениях уже на текущей итерации.

Асинхронные модели отражают не только логические функции, но и временные задержки в распространении сигналов.

Синхронные модели можно использовать не только для выяв­ле­ния принципиальных ошибок в схемной реализации заданных функ­ций. С их помощью можно обнаруживать места в схемах, опас­ные с точки зрения возникновения в них искажающих помех. Си­туации, связанные с потенциальной опасностью возникновения помех и сбоев, называют рисками сбоя.

При использовании асинхронных моделей возможны два метода моделирования – пошаговый (инкрементный) и событийный. В поша­го­вом методе время дискретизируется и вычисления выпол­ня­ются в дискретные моменты времени t₀,t₁,t₂,…и т.д.

Для сокращения времени анализа используют событийный ме­тод. В этом методе событием называют изменение любой переменной математической модели.

Математические модели анализа проектных решений на систем­ном уровне. Объектами анализа на системном уровне явля­ют­ся такие сложные системы, как производственные предприятия, сис­темы магистрального транспорта газа, нефтедобывающие пред­при­ятия, автоматизированные технологичес­кие комплексы, вычисли­тельные системы и сети и т.д.

Для многих объектов анализ проектных решений на системном уровне связан с исследованием прохождения через систему или её подсистемы потока заявок (иначе называемых требованиями или транзактами). Оцениваются такие параметры, как произво­ди­тель­ность (пропускная способность) проектируемой системы, продолжи­-

тельность обслуживания заявок в системе, достаточность выбранного оборудования, эффективность использования оборудования в систе­ме. Заявками могут быть клиенты в банках; грузы, поступающие на погрузку; задачи, решаемые в вычислительной системе; самолёты, подлетающие к аэропорту и т.д.

Параметры заявок, поступающих в систему, являются случай­ными величинами, и при проектировании могут использоваться их за­ко­­ны распределения. Поэтому анализ на системном уровне, как пра­ви­­ло, носит статистический характер. В качестве математического аппарата моделирования применяется теория массового обслужи­ва­ния, а проектируемые объекты рассматриваются как системы мас­сового обслуживания (СМО).

Выходными параметрами в СМО являются числовые харак­те­ристики таких величин, как время обслуживания заявок в системе, длины очередей заявок на входах, время ожидания обслу­жи­вания в оче­редях, загрузка устройств системы, вероятность обслужи­вания в заданные сроки и т.д.

Элементами систем массового обслуживания являются:

- источник требований (заявок);

- входящий поток требований;

- очередь;

- обслуживающее устройство (аппарат) или канал обслуживания;

- выходящий поток требований.

СМО классифицируют по разным признакам. По такому признаку, как условия ожидания требованием начала обслуживания, различают следующие виды систем массового обслуживания:

- с потерями (с отказами);

- с ожиданием;

- с ограниченной длиной очереди;

- с ограниченным временем ожидания.

СМО, у которых требования, поступающие в моменты загру­жен­ности всех приборов обслуживания, получают отказ и теряются, на­зываются системами с потерями или отказами.

СМО, у которой возможно появление какой угодно длинной оче­реди требований к обслуживающему устройству, называются сис­те­мами с ожиданием.

СМО, допускающие очередь, но с ограниченным числом мест в ней, называются системами с ограниченной длиной очереди.

СМО, допускающие очередь, но с ограниченным сроком пребы­ва­ния каждого требования в ней, называются системами с огра­ни­ченным временем ожидания.

По числу каналов (приборов) СМО делятся на одноканальные и многоканальные.

Правило, по которому заявки выбираются из очередей на обслу­живание, называют дисциплиной обслуживания, а величину, вы­ра­жающую преимущественное право на обслуживание, - прио­ритетом. В бесприоритетных системах все транзакты имеют одинаковые приоритеты. Среди бесприоритетных приме­ня­ются дисциплины: первым пришёл–первым обслужен, пос­лед­ним пришёл-первым обслужен и со случайным выбором заявок из очереди.

При анализе СМО определяют показатели эффективности сис­темы, состоящие из двух групп.

Показатели первой группы определяют на основе значений веро­ятностей состояний системы.

1. Вероятность того, что поступающее в систему требование от­ка­жется присоединяться к очереди и будет потеряно (Р_отк). Этот по­ка­затель для системы с отказами равен вероятности того, что в системе находится столько требований, сколько она содержит кана­лов обслу­живания:

Р_отк=Р_m , (7.10)

где m-число каналов обслуживания.

Для системы с ограниченной длиной очереди Р_отк равна веро­ят­ности того, что в системе находится m+l требований:

Р_отк=Р_m+l , (7.11)

где l- допустимая длина очереди.

2. Среднее количество требований, ожидающих начала обслу­живания,

, (7.12)

где P_n - вероятность того, что в системе находится n требований.

При условии простейшего потока требований и экспонен­ци­аль­ного закона распределения времени обслуживания формулы для М_ож принимают следующий вид:

- система с ограниченной длиной очереди

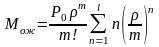, (7.13)

где интенсивность входящего потока требований (среднее число

требований, поступающее в единицу времени);

μ- интенсивность обслуживания (среднее число обслуженных

требований в единицу времени);

.

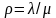- система с ожиданием

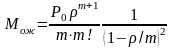. (7.14)

3. Относительная пропускная способность системы

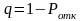. (7.15)

4. Абсолютная пропускная способность системы

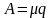. (7.16)

5. Среднее число занятых обслуживанием приборов

. (7.17)

Для системы с отказами m_з находится как

. (7.18)

6. Общее количество требований, находящихся в системе:

- система с отказами 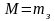; (7.19)

- система с ограниченной длиной очереди

. (7.20)

7. Среднее время ожидания требованием начала обслуживания. Если известна функция распределения вероятностей времени ожида­ния требованием начала обслуживания 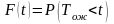, то среднее вре­мя ожидания находится как математическое ожидание случайной величины Т_ож:

; (7.21)

при показательном законе распределения требований во вхо­дя­щем потоке

. (7.22)

Показатели второй группы характеризуют экономические осо­бен­ности системы. Одним из таких показателей является эконо­ми­ческая эффективность системы

, (7.23)

где с – средний экономический эффект, полученный при обслу­жи­вании одного требования;

Т – рассматриваемый интервал времени;

G_П - величина потерь в системе.

Величину потерь можно определить по следующим формулам:

- система с отказами

, (7.24)

где 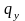- стоимость убытков в результате ухода требований из систе-

­­­­­­­­мы в единицу времени;

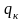- стоимость эксплуатации одного канала в единицу времени;

- стоимость единицы времени простоя канала;

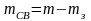- число свободных каналов.

- система с ожиданием

, (7.25)

где - стоимость потерь, связанных с простоем требований в оче­

реди в единицу времени.

Для анализа СМО применяют аналитическое и имитационное моделирование.

Аналитическое моделирование предполагает получение формулы для расчёта выходных параметров СМО с последующими вычис­лениями по этим формулам. Аналитическое исследование удаётся реа­лизовать только для сравнительно не сложных СМО.

Поэтому основным подходом по анализу на системном уровне проектирования является имитационное моделирование.

Аналитические модели СМО. Аналитические модели удаётся получить при серьёзных допущениях.

Во-первых, считают, что в СМО используются бесприоритетные дисциплины обслуживания типа первым пришёл – первый обслужен.

Во-вторых, времена обслуживания заявок в устройствах выбира­ются в соответствии с экспоненциальным законом распределения.

В-третьих, считают, что выходные потоки заявок являются прос­тейшими потоками, т.е. обладают свойствами стационарности, орди­нарности (невозможности одновременного поступления двух заявок на вход СМО), отсутствия последействия.

Рассмотрим СМО с отказами. Граф состояний многоканальной СМО с отказами имеет вид, изображённый на рис.7.3. Здесь λ – интенсивность входящего потока требований; μ –производительность одного канала обслуживания; s₀,s₁,…,s_m – состояния системы (индекс указывает число требований в системе); m – общее число каналов.

Рис.7.3. Граф состояний многоканальной СМО с отказами

Вероятности состояний системы с отказами определяют по формулам

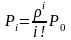; (7.26)

где ;

i=1,2,…m,

а вероятность Р₀ (вероятность того, что все каналы обслуживания свободны) находят из выражения

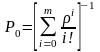. (7.27)

Если заняты все m каналов обслуживания, то вновь поступившее требование не обслуживается и покидает систему. При этом вероят­ность отказа по формуле (7.26) определяется как

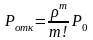. (7.28)

Среднее число занятых обслуживанием приборов для системы с отказами можно найти по формуле

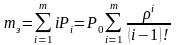. (7.29)

Рассмотрим СМО с ожиданием. Граф состояний много­каналь­ной СМО с ожиданием изображён на рис.7.4.

Рис.7.4. Граф состояний многоканальной СМО с ожиданием

На рис.7.4: λ –интенсивность входящего потока требований; μ – производительность одного прибора (устройства) обслуживания; m – общее число каналов; s₀,s₁,s₂,…s_m,…s_m+к – состояния системы (индекс указывает число требований в системе).

Вероятности состояния s₀,s₁,s₂,…s_m системы с ожиданием находят по формулам

, (7.30)

где i=1,2,…m.

Вероятности состояний s_m+1,…s_m+k,…системы с ожиданием находят по формулам

P₀, (7.31)

где i=m=1,…m+k,…

При вероятность того, что все каналы обслуживания свободны, определяется как

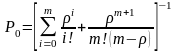. (7.32)

Среднее число занятых обслуживанием приборов в случае экспонен­циального характера потока требований и времени ожидания находится как

_. (7.33)

Для СМО с ожиданием q=1 (смотри формулу 7.15). Поэтому среднее число занятых обслуживанием приборов

.

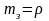Для СМО с ожиданием среднее число требований, ожидающих начала обслуживания, определяется как

. (7.34)

Для СМО с ожиданием среднее время ожидания требования начала обслуживания находится как

. (7.35)

Имитационные модели СМО. Для имитационных моделей СМО могут использоваться языки программирования общего при­ме­нения, однако такие пред­ставления оказываются довольно громозд­кими. Поэтому обычно используют специальные методы и языки имитационного моделирования для анализа проектных решений на сис­темном уровне.

Для описания имитационных моделей на системном уровне используют языки, ориентированные на события или процессы.

Событийный метод моделирования. Сущность событийного метода заключается в отслеживании на модели последовательности событий в том же порядке, в каком они происходят в реальной системе. Вычисления выполняются для тех моментов времени и тех частей модели, к которым отно­сятся совершаемые события. Другими словами, обращения на очередном такте моделируемого времени осуществляется только к моделям тех элементов (устройств, частей объекта), на входах которых в этом такте произошли изменения.

Сформулировать единый критерий оптимальности проектируе­мого объекта и решить задачу синтеза его по этому критерию в боль­шинстве случаев не представляется воз­мож­ным. Поэтому общая задача синтеза объекта разбивается на ряд подзадач: разработка фун­к­­циональной схемы; определение структуры объекта; определение па­­ра­метров объекта; выбор элементов; конструирование аппаратуры.

Если при формализации задачи синтеза удалось все проектные па­раметры представить в числовом виде, то можно применить методы математического программирования.

Однако применение точных методов математического прог­раммирования при синтезе структуры объекта сопряжено с большими трудностями. Поэтому при синтезе структуры объекта лидирующее положение занимают приближённые методы. Широко применяются операции разделения множества вариантов на подмножества и отсе­че­ние неперспективных подмножеств. Эти методы объединяются под названием метода ветвей и границ.

К математическому обеспечению анализа относятся математичес­кие модели анализа проектных решений, численные методы и алго­рит­­мы выполнения проектных процедур анализа. Цель анализа – по­лу­­­че­­ние информации о характере функциони­ро­­­вания объекта, о зна­чениях выходных параметров при синтезиро­ванной структуре объек­та, сведения о значениях параметров элемен­тов объекта.

Системы автоматизированного проектирования осуществляют ана­­­лиз проектных решений на микроуровне, макроуровне, функ­цио­нально-логическом уровне и на системном уровне. При этом на раз­ных иерархических уровнях проектирования для построения матема­тических моделей анализа проектных решений используется различ­ный математический аппарат (сеточные методы, компонентные и топологические уравнения проектируемого объекта, аппарата передаточ­ных функций, теория массового обслужи­ва­ния).

Заключение

В лекции дано определение проектной процедуры, называемой структурным синтезом. Отмечено, что задачи структурного синтеза от­­­носятся к трудно формализуемым. По этой причине структурный синтез, как правило, выполняют в интерактивном режиме при решаю­щей роли проектировщика, а ЭВМ играет вспомогательную роль.

Если при формализации задачи синтеза удалось все проектные параметры представить в числовом виде, то можно применить мето­ды математического программирования.

Рассмотрены цели параметрического синтеза. Задача параметри­ческого синтеза может быть сформулирована как задача определения значений параметров элементов.

Рассмотрены этапы разработки математической модели анализа проектных решений.

Вопросы для самопроверки

1. На какие подзадачи разбивается общая задача синтеза объекта?

2. Как решаются задачи структурного синтеза?

3. В чём заключается цель параметрического синтеза?

4. Какие данные являются исходными в задачах синтеза структуры автоматизированной системы управления?

5. Из каких этапов состоит работа по разработке математической модели анализа проектных решений?

6. Примеры объектов анализа проектных решений на микроуровне?

7. Какие уравнения называются компонентными в математических моде­лях анализа на макроуровне?

8. Какие уравнения называют топологическими в математических моде­лях анализа на макроуровне?

9. Как осуществляется многовариантный анализ на макроуровне?

10. Как осуществляется моделирование аналоговых объектов (устройств) на функционально-логическом уровне?

11. Как осуществляется моделирование дискретных объектов (устройств) на функционально-логическом уровне?

12. Для каких объектов, систем, процессов необходим анализ на системном уровне?

13. Перечислите элементы системы массового обслуживания.

14. Перечислите виды систем массового обслуживания.

15. Назовите показатели эффективности систем массового обслуживания.

16. Рассмотрите систему массового обслуживания с отказами.

17. Рассмотрите систему массового обслуживания с ожиданием.

Лекция 8. Машинная графика и геометрическое моделирование в САПР

План лекции

В лекции будут рассмотрены следующие вопросы:

- двумерное и трёхмерное проектирование в САПР;

- графический редактор AutoCAD;

- графический редактор КОМПАС-3D.

Литература: Л.6, Л.7, Л.8.

8.1. Двумерное и трёхмерное проектирование в САПР

Прежде чем изготовить промышленное изделие (автомобиль, станок, самолёт, корабль и т.д.), конструктор должен наглядно изо­бразить этот объект, который ещё не существует. Другими словами, проектно-конструкторский процесс определяет будущее изделие.

Конструирование разделяют на два вида деятельности: эскизное проектирование и конструкторская разработка.

При эскизном проектировании определяется принцип действия раз­рабатываемого изделия, изучаются аналоги. На этапе кон­стру­иро­вания разрабатывается полный комплект технической документации (чертежи нового изделия или нового технологического процесса, рас­чёты, сметы, спецификации и т.д.). Техническая документация дол­жна быть достаточна для изготовления конструируемого изделия.

При конструировании нового изделия важный и трудоёмкий вид работ – это разработка инженерно-графической документации.

Издавна чертёж выполняется с использованием чертёжных ин­струментов (линейки, треугольника, циркуля) на планшете (чер­тёжной доске). При этом точность выполнения чертежа зависит от квалификации конструктора и остроты его зрения.

Применение САПР позволяет сократить продолжительность про­ект­но-конструкторских работ, потому что к возможностям САПР относятся:

- более быстрое выполнение чертежей;

- повышение точности выполнения чертежей;

- повышение качества выполнения чертежей;

- возможность многократного использования чертежа. Изобра­же­ние всего чертежа или его части можно сохранить для дальнейшей работы. Сохранённый чертёж может быть использован для последую­щего проектирования.

Различают математическое обеспечение двумерного (2D) и трёхмерного (3D) моделирования.

Основные применения 2D-графики – подготовка чертёжной доку­мен­тации в машиностроительных САПР, топологическое проекти­ро­вание печатных плат, автоматизированное проектирование маги­страль­ных нефтепроводов и газопроводов и т.д.

Трёхмерные системы (3D) используются для синтеза конструк­ций в машиностроении и проектирования строительных сооружений. Эти системы позволяют имитировать перемещение в пространстве рабочих органов изделия (например, манипуляторов робота). Они позволяют отслеживать траекторию движения инструмента при раз­ра­ботке технологического процесса изготовления деталей на станоч­ном оборудовании различного типа.

Двумерные системы (2D). Системы двумерного моделирования распознают геометрические формы, определяемые точками, прямыми или кривыми на плоскости. С помощью двумерных систем создаётся большинство конструкторских документов.

Все команды любой двумерной системы можно разделить на три вида:

- команды черчения;

- команды редактирования;

- команды нанесения размеров, условных обозначений и текста (оформления чертежа).

8.2. Графические редакторы системы AutoCAD

AutoCAD пред­став­ляет собой систему, позволяющую автома­ти­зировать чер­тёжно-графические работы. В графическом пакете AutuCAD есть всё, что необходимо конструктору для создания чертежа.

Инструментам черчения в автоматизированной среде соответ­ствуют графические примитивы (точка, отрезок, окружность и др.), команды их редактирования (стирание, перенос, копирование и т д.), команды установки свойств примитива (задание толщины, типа и цвета графических объектов). Для выбора листа нужного формата и масштаба чертежа в системе есть команды настройки чертежа.

Для нанесения размера конструктору необходимо задать место его расположения на чертеже. Размерная и выносная линии, а также стрелки и надписи выполняются автоматически.

Соответствующие команды AutoCAD позволяют увеличивать изображение на экране или уменьшать его при необходимости.

Система позволяет хранить графические объекты под определён­ными номерами и при необходимости вставлять их в любой чертёж, что избавляет конструктора от вычерчивания части повторяющихся элементов чертежа.

Чертить в системе AutoCAD – значит формировать на экране дис­плея изображение из отдельных графических элементов (прими­ти­вов), которые вводятся при помощи соответствующих команд графи­ческого интерфейса.

Ввод команд и графических элементов осуществляется при помо­щи мыши или клавиатуры.

8.3. Система КОМПАС-3D

Программный пакет КОМПАС-3D можно разделить на три большие составляющие:

- КОМПАС-График – чертёжно-графический редактор;

- КОМПАС-3D – модуль для работы с трёхмерными моделями;

- редактор спецификаций и текстовых документов.

Каждой составляющей соответствуют свои типы файлов, а каж­дому типу файлов – отдельный значок и собственное расширение.

При первом запуске КОМПАС выводит на экран стартовую стра­ницу, на которой отображено несколько ссылок, используя которые можно выполнить следующие действия:

- Учебное пособие «Азбука КОМПАС» - доступ к интер­актив­но­му учебному пособию, позволяющему самостоятельно освоить от­дельные приёмы работы с программой;

- Форум пользователей КОМПАС – перейти на интернет-стра­ницу форума пользователей системы КОМПАС, где вы можете задать интересующий вас вопрос;

- Сайт Службы технической поддержки – перейти на сайт службы технической поддержки, где вы можете обратиться за помо­щью к специалисту.

КОМПАС-График. Представляет различные решения для дву­мер­ного проектирования. КОМПАС-График полностью поддержи­вает отечественные стандарты ЕСКД или СПДС на оформление конструкторской документации. Начиная с версии V8 Plus, КОМПАС обеспечивает поддержку и международного стандарта ISO. Предус­мотрен набор типов основных надписей, исполь­зую­щихся в машино­строении, строительстве и т.д.

Работа в КОМПАС-График реализована через два типа доку­ментов: КОМПАС-Фрагмент и КОМПАС-Чертёж.

КОМПАС-Фрагмент используется как вспомогательный доку­мент, позволяя сохранять отдельно от чертежа различные его части.

Все команды, предназначенные для создания различных геомет­рических объектов на чертеже, объединены на панели инструментов Геометрия. Большинство команд этой панели объединено в группы по своему функциональному назначению.

Для доступа к командам следует щёлкнуть кнопкой мыши и удер­живать её на кнопке группы, пока не раскроется панель с командами данной группы, после чего можно выбрать любую из них.

Перечислим группы команд:

- для создания точки;

- для построения отрезков;

- для построения окружностей;

- для построения эллипсов.

При построении окружностей и эллипсов есть возможность включить режим автоматического построения осевых линий.

Кроме того, имеются команды для построения многоугольников, выполнения штриховки (различного стиля), заливки и ряд других.

Система КОМПАС-График содержит большой набор средств для создания размеров и различных знаков-обозначений.

Кнопки для вызова команд простановки размеров собраны на панели инструментов Размеры.

Кнопки предлагают все возможные варианты нанесения размеров (линейный, угловой, радиальный, размер дуги окружности и пр.). Доступны различные параметры отображения размера и размерной надписи (параллельно над линией, в разрыве линии и т.д.). Предус­мотрен выбор типа стрелки на концах размерной линии.

Приведём определения некоторых понятий:

- Чертёж – главный графический документ системы КОМПАС-3D, хранящий информацию об изображении, оформлении и прочих элементах конструкторского документа;

- Вид – часть изображения чертежа;

- Оформление чертежа – различные элементы чертежа (основ­ная надпись, рамка, технические требования и т.д.), которые, как правило, должны присутствовать обязательно.

КОМПАС-3D – модуль для работы с трёхмерными моделями. Переворотом в промышленном проектировании стало применение в конструировании трёхмерной графики. Кроме лучшего визуального представления проектируемых изделий, 3D-графика повышает точность проектирования особенно сложных (составных) объектов, позволяет легко редактировать трёхмерную модель.

Значительную долю среди программных средств для автомати­за­ции инженерного проектирования занимают графические CAD-систе­мы. Они служат для создания трёхмерных моделей машинострои­тель­ных агрегатов, изделий, зданий и т.д., формирования и офор­мления комплекта чертежей вместе с полным набором конструк­торской документации, необходимой для выпуска изделия или сооружения объекта.

Помимо лучшего визуального представления (по сравнению с плоским изображением), трёхмерные модели удобно использовать в инженерных расчётах. Для этого существует другой класс инжене­р­ных систем проектирования - CAE-системы. Расчёты прочности, ки­не­ма­тика и динамика, аэродинамические и гидравлические расчёты и многое другое стало доступным и простым с появлением систем та­ко­го класса. Инженер получает инструмент – трёхмерное пред­став­ление напряжений в изделии, объёмное распределение температур, пространственное моделирование потоков газов, жидкостей и их смесей. Кроме того, трёхмерная модель всегда более точно описывает объект, чем самое подробное двухмерное изображение.

Моделирование – сложный процесс, результатом которого является законченная трёхмерная сцена (модель объекта) в памяти компьютера. Моделирование состоит из создания отдельных объек­тов сцены с их последующим размещением в пространстве.

Рассмотрим основные подходы, предлагаемые в программах 3D-графики для выполнения трёхмерных моделей объектов:

- создание твёрдых тел с помощью булевых операций – путём добавления, вычитания или пересечения материала моделей;

- формирование сложных полигональных поверхностей, так называемых мешей (от английского mesh-сетка), путём полиго­наль­ного или NURBS-моделирования;

- применение модификаторов геометрии (используются в основ­ном в дизайнерских системах моделирования). Модификатором назы­вается действие, назначаемое пользователем, в результате чего свой­ства объекта и его внешний вид изменяются. Модификатором может быть вытягивание, изгиб, скручивание и т.п.

КОМПАС-3D – это система твёрдотельного моделирования. Это значит, что операции по созданию и редактированию трёхмерных моделей предназначены только для работы с твёрдыми телами.

Твёрдое тело – область трёхмерного пространства, состоящая из однородного материала и ограниченная замкнутой поверхностью, ко­торая сформирована из одной или нескольких стыкующихся граней.

Грань – гладкая (не обязательно плоская) часть поверхности де­та­­ли, ограниченная замкнутым контуром из рёбер. Частный случай – шарообразные твёрдые тела и тела вращения с гладким профилем, состоящие из единой грани, которая, естественно, не имеет рёбер.

Ребро – пространственная кривая произвольной конфигурации, полученная на пересечении двух граней.

Вершина – точка в трёхмерном пространстве. Для твёрдого тела это может быть одна из точек на конце ребра.

В КОМПАС любое изменение формы детали называется трёхмерной формообразующей операцией или просто операцией.

Формировать модель в КОМПАС-3D можно в двух типах документов: КОМПАС-Деталь и КОМПАС-Сборка.

Документ Деталь предназначен для создания с помощью формообразующих операций и хранения модели целостного объекта (простого изделия, отдельной детали, компонента). Однако не обяза­тельно, чтобы модель в документе КОМПАС-Деталь соответ­ство­вала реальной единичной детали. Например, в качестве единой детали может быть представлена трёхмерная модель подшип­ника, в дей­ствительности состоящего из нескольких деталей.

В документе Сборка собираются в единый агрегат смодели­ро­ванные и сохранённые ранее детали. Эти детали вначале размещают в пространстве, сопрягают вместе и фиксируют.

При выполнении операций в детали возможен выбор нескольких вариантов (режимов) построения:

- при вырезании (удалении материала):

- вычитание элемента – удаление материала детали происходит внутри замкнутой поверхности;

- пересечение элементов – удаление материала детали, находя­ще­гося снаружи поверхности, которая сформирована в результате опе­рации;

- при «приклеивании» (добавление материала):

- новое тело – добавляемый трёхмерный элемент формирует в де­та­­ли новое твёрдое тело независимо от того, пересекается он с уже существующими телами или нет;

- объединение – добавляемый элемент соединяется с твёрдым те­лом, с которым он пересекается;

- автообъединение – при этом система автоматически объединяет в одно тело существующий и новые элементы, если они пересе­ка­ются, или формирует новое тело, если они не пересекаются.

Формообразующие операции (построение деталей). Большин­ство операций по созданию моделей основывается на эскизах.

Эскиз – это двумерное изображение, размещённое на плоскости в трёхмерном пространстве. В эскизе могут присутствовать любые графические элементы (примитивы), за исключение элементов оформления (обозначений) конструкторского чертежа и штриховки. Эскизом может быть как замкнутый контур или несколько контуров, так и произвольная кривая.

Последовательность построения эскиза для формообразующей операции:

1. Выделите в дереве построения или в окне документа плоскость, на которой планируете поместить эскиз. Если в модели уже есть какое-либо тело (или тела), вы можете в качестве опорной плоскости эскиза использовать любую из его плоских граней. Выделить плоскую грань можно только в окне представления документа.

2. Нажмите кнопку Эскиз на панели инструментов Текущее состояние. Модель плавно изменит ориентацию таким образом, чтобы выбранная вами плоскость разместилась параллельно экрану.

3. После запуска процесса создания эскиза контактная панель изменит свой вид. На ней будут расположены панели инстру­ментов, свойственные как трёхмерным, так и графическим документам системы КОМПАС-3D. Пользуясь командами для двумерных построений, создайте изображение в эскизе. Для завершения создания или редактирования эскиза отожмите кнопку Эскиз.

4. Эскиз останется выделенным в окне документа (подсвечен зелё­ным цветом), поэтому можно вызвать нужную команду и соз­давать или вносить изменения в геометрию модели.

Существует четыре основных подхода к формированию трёх­мер­ных элементов. Рассмотрим их.

- Выдавливание. Форма трёхмерного элемента образуется пу­тём смещения эскиза операции строго по нормали к его плоскос­ти. Во время выдавливания можно задать уклоны внутрь или наружу.

- Вращение. Формообразующий элемент является результатом вращения эскиза в пространстве вокруг произвольной оси.

- Кинематическая операция. Поверхность элемента формиру­ется в результате перемещения эскиза операции вдоль произ­вольной трёхмерной кривой. Эскиз должен содержать обя­за­тельно замкнутый контур, а траектория перемещения – брать начало в плоскости эскиза. Траектория не должна иметь разрывов.

- Операция по сечениям. Трёхмерный элемент создаётся по нескольким сечениям – эскизам. Эскизов может быть сколько угодно, и они могут быть размещены в произвольно ориентированных плоскостях.

Все команды для построения и редактирования детали распо­ложены на панели инструментов Редактирование дета­ли. Для пере­хода к этой панели надо щёлкнуть на одноимённой кнопке ком­пактной панели. При этом активным должен быть документ КОМПАС-Деталь.

Подобно прочим панелям инструментов, панель Редактирование детали содержит как одиночные кнопки, так и группы кнопок.

Первой идёт группа кнопок, позволяющих добавить материал детали (или создать основание). В неё входят следующие команды:

- Операция выдавливания;

- Операция вращения;

- Кинематическая операция;

- Операция по сечениям.

Все эти команды отвечают определённому способу построения формы твёрдого тела. Как правило, с одной из этих команд начинается построение твёрдого тела.

Ещё одной операцией, с которой начинается построение детали, является Деталь-заготовка. Её кнопка следует сразу за группой команд добавления материала. Эта команда позволяет использовать в качестве заготовки другую ранее построенную и сохранённую деталь.

После вставки детали-заготовки в новый документ можно продолжить построение или редактирование заготовки так же, как если было бы создано основание при помощи операции выдавливания.

Далее идёт группа команд удаления материала детали (команды вырезания):

- вырезать выдавливанием;

- вырезать вращением;

- вырезать кинематически;

- вырезать по сечениям.

Итак, принцип создания трёхмерных моделей в КОМПАС: всё построение детали состоит из последовательного рисования эскизов и выполнения над ними формообразующих операций. Однако недоста­точно использовать в качестве опорных только ортогональные плос­кости.

Как угодно разместить в пространстве плоскости для эскиза можно, используя вспомогательные объекты.

Предусмотрено несколько типов вспомогательных объектов. Основные из них – конструктивные плоскости и конструктивные оси.

Конструктивные плоскости служат для определённого размещения эскиза в пространстве.

Конструктивные оси используются при создании массивов элементов.

Команды для создания перечисленных элементов находятся на панели инструментов «Вспомогательная геометрия».

Свойства трёхмерных объектов. Все трёхмерные объекты КОМПАС-3D наделены определёнными свойствами:

- наименование – это название трёхмерного объекта (эскиза, операции, детали и пр.);

- видимость – это свойство управляет отображением трёхмер­ного объекта в документе (скрытый или видимый);

- состояние – любой объект включён или исключён из расчёта;

- цвет – задаёт цвет объекта в модели.

Построение сборочной единицы. Сборочная единица (сборка) – это трёхмерная модель объекта, объединяющая модели деталей и стандартных изделий. Количество деталей в сборке не ограничено.

Компонентом сборки может быть твёрдотельная или листовая деталь, вставленная в сборку или созданная прямо в ней, деталь или поверхность, импортированные из другой системы трёхмерного моделирования (с помощью одного из обменных форматов), а также другая сборка (она называется подсборкой).

В сборке можно выполнять формообразующие операции, которые используются при построении деталей.

Процесс формирования трёхмерной сборки в системе КОМПАС-3D состоит из нескольких этапов.

1. Вставка компонентов сборки (отдельных деталей из файлов или стандартных элементов из библиотек). Отдельные компоненты могут создаваться прямо в сборке.

2. Размещение каждого компонента определённым образом и задание нужной ориентации в пространстве сборки.

3. Создание отдельных деталей прямо в сборке.

4. Применение завершающих операций, таких как создание отверстий, фасок и пр.

Чаще всего вставка и размещение компонентов выполняются одновременно.

Основные команды для управления объектами сборки размещены на панели инструментов Редактирование сборки.

Первой идёт группа кнопок, содержащая всего две команды для создания компонентов сборки непосредственно в текущей сборке. Команда Создать деталь служит для построения детали в режиме редактирования детали в сборке.

Вторая команда этой группы – Создать сборку. После нажатия данной кнопки система перейдёт в режим редактирования, только уже не детали в сборке, а подсборки в текущей сборке.

Для изменения положения компонента в сборке существуют команды перемещения и поворота.

Последняя команда панели инструментов Редактирование сборки-Новый чертёж из модели. Она создаёт новый документ КОМПАС-Чертёж, содержащий ассоциативный вид с модели, для которой эта команда была вызвана.

В условиях динамично развивающихся систем автоматизированного проектирования знание основ машинной графики и геометрического моделирования, методов создания чертежей является необходимым для современного инженера.

В любой проектной и конструкторской организации, на любом предприятии последние несколько лет большое внимание уделяется подготовке расчётов, чертежей и различной документации с использованием средств вычислительной техники.

Современный инженер, кроме знаний в своей области, должен владеть навыками автоматизированного проектирования, легко, точно и быстро с помощью компьютеров выполнять работы по расчётам, по проектированию и конструированию объектов, по разработке документации.

Заключение

В лекции приводятся примеры применения 2D-графики и трёх­мерных систем (3D).

Рассмотрены графические редакторы системы AutoCAD. Auto­CAD представляет собой систему, позволяющую автоматизиро­вать чертёжно-графические работы. Чертить в системе AutoCAD – значит формировать на экране изображение из отдельных графических эле­ментов.

Рассматривается система КОМПАС-3D. Указывается, что пакет КОМПАС-3D можно разделить на три составляющие:

- КОМПАС-ГРАФИК;

- КОМПАС-3D – модуль для работы с трёхмерными моделями;

- редактор спецификаций и текстовых документов.

В условиях развивающихся систем автоматизированного проек­ти­­рования знание основ машинной графики и геометрического моде­лирования, методов создания чертежей являются необходимыми для современного инженера.

Вопросы для самопроверки

1. За счёт чего при применении САПР сокращается продолжительность проектно-конструкторских работ?

2. Основные применения 2D-графики?

3. Основные применения 3D-графики?

4. Что собой представляют графические редакторы системы AutoCAD?

5. Из каких компонентов состоит программный пакет КОМПАС-3D?

6. Какие задачи могут быть решены при помощи чертёжно-графического редактора КОМПАС-График?

7. Какие задачи могут быть решены при помощи модуля КОМПАС-3D?

8. Какие операции выполняются при конструировании детали?

9. Какие операции выполняются при конструировании сборочной единицы?

10. Что представляет собой компонент сборки?

Лекция 9. Информационное обеспечение САПР.

Организационное и методическое обеспечение САПР

План лекции

В лекции будут рассмотрены следующие вопросы:

- информационное обеспечение САПР;

- организационное и методическое обеспечение САПР;

- автоматизированное проектирование систем автома­ти­чес­ко­го уп­­­­равления;

- автоматизированное проектирование АСУТП.

Литература: Л.3, Л.4.

9.1. Информационное обеспечение САПР

Определение 9.1. Информационное обеспечение САПР – это совокупность документов, содержащих следующую информацию:

- о проектных процедурах;

- о типовых проектных решениях;

- данные о ранее выпущенных проектах в данной предметной области;

- данные о комплектующих изделиях;

- данные о материалах, которые могут быть использованы при строи­тель­стве, сооружении или изготовлении проектируемого объекта;

- и т.д.

Множество данных, которые используются при функционировании САПР, образует базу данных (БД) системы. БД САПР является основной частью ин­фор­­мационного обеспечения системы автоматизированного проектирования.

Определение 9.2. База данных САПР – это совокупность данных неко­торой предметной области, определяемой свойствами и харак­теристиками про­ектируемых объектов.

Замечание 9.1. Абонентами БД САПР, т.е. информационного обеспечения системы, являются проектировщики (конструктора) и программные модули.

Проектировщики используют БД в итерационном диалоговом режиме, поэ­тому БД должна быть разработана таким образом, чтобы затраты времени на поиск необходимых данных были минимальными.

Замечание 9.2. БД САПР является основным связующим звеном между отдельными проектными процедурами, операциями, задачами.

Основные требования к информационному обеспечению САПР:

1. Наличие необходимой информации для обеспечения как автома­тизированных, так и ручных процедур проектирования.

2. Возможность хранения и поиска информации, представляющей результат выполнения автоматизированных и ручных процедур проектирования.

3. Достаточный объём памяти с возможностью её наращивания вместе с увеличением объёма информации, подлежащей хранению.

4. Необходимость обеспечить сжатие и архивирование хранимой информации, т.е. обеспечить её компактное хранение.

5. Должна быть обеспечена быстрая реакция на обращения и запросы.

6. Возможность быстрого внесения изменений в хранимую информацию, т.е. осуществление процедур корректировки.

7. Обеспечение возможности получения твёрдых копий по всем данным информационного обеспечения.

Интерфейс обеспечивает взаимодействие базы данных САПР с про­­­г­­­­раммами для выполнения проектных операций (для решения про­­­­­ектных задач) и с проектировщиками (рис.9.1). В функции ин­тер­­­фейса входит согласование и сопряжение БД САПР с прог­рам­ма­ми и проектировщиками по форматам записей (информационный ас­пект), по обозначениям данных (содержательный аспект) и по программным ­­­средствам (программный аспект). Информация, образую­щая ин­­фор­ма­­­ционное обеспечение системы, может быть классифи­ци­ро­вана по нескольким признакам. По кратности применения ин­фор­­мация может быть подразделена на общую и частную.

Определение 9.3. Общая информация – это информация много­разового применения. Эта информация используется для разработки целого ряда проектов в данной предметной области.

Рис.9.1. Место базы данных в системе автоматизированного

проектирования

Определение 9.4. Частная информация – это информация, пред­назначенная для применения при проектировании только одного объекта (при работе над одним проектом).

По характеру изменения во времени информация САПР может быть подразделена на статическую и динамическую.

Определение 9.5. Статическая информация – это информация сис­те­мы, характеризующаяся сравнительно редкими изменениями. К этой информации относятся справочные данные, информация о дей­ствую­­щих стандартах, о типовых решениях в данной предметной об­ла­сти, о ранее выполненных проектах и разработках.

Определение 9.6. Динамическая информация – это промежу­точ­ные данные, накапливаемые при выполнении определённых проект­ных процедур и операций, а также информация в виде результатов выполнения проектной работы; промежуточная информация в про­цес­се проектирования постоянно пополняется.

Формирование, загрузка и корректировка справочной информации осуществляется исключительно администратором базы данных. Ад­ми­нистратор базы данных САПР поддерживает непосредственный контакт со службой нормализации и стандартизации проектной орга­ни­зации.

В состав статической информации входят нормативные документы (законы, руководящие документы, постановления, ГОСТы, стандар­ты, ценники, информационные материалы фирм-производителей де­та­лей, модулей, приборов ит.д., методики, инструкции, типовые про­екты, проекты-аналоги и т.д.).

По виду представления информации САПР может быть подраз­делена на документальную, иконографическую и фактогра­фи­чес­­кую.

Определение 9.7. Документальная информация системы – это ин­фор­мация об аналогичных объектах в данной предметной области, о патентах, методиках проектирования и расчётов и т.д.

Определение 9.8. Иконографическая информация – это инфор­мация в виде чертежей, фотографий, графиков.

Определение 9.9. Фактографическая информация – это числовые и текстовые данные о комплектующих деталях, материалах, ценах, нор­мах, стандартах, о полученных результатах при проектировании; данные, необходимые для выполнения расчётов: коэффициенты, таблицы, аппроксимированные графические зависимости и т.д.

На рис.9.2 показана схема информационных потоков САПР. Здесь: ТЗ – техническое задание на выполнение проектной или кон­струк­торской работы; ППП i- программа i-ой проектной процедуры (решение системой i-ой проектной задачи).

База данных САПР представляет собой совокупность частей – подмножеств базы данных. Пользуясь символикой теории множеств, обозначим БД САПР как объединение некоторого числа частей – подмножеств базы данных:

,

где - символ объединения подмножеств;

n – число частей (подмножеств) данной БД САПР.

Рис.9.2. Схема информационных потоков САПР

Назовём ту часть БД, в которой содержится информация мно­горазового при­менения, т.е. общая информация, системной частью базы данных (СЧ БД).

Приступая к разработке проекта, в САПР вводят исходные сведения (ТЗ, сро­ки выполнения проекта и т.д.). На основании исходных данных САПР формулирует подмножество БД для данного конкретного объекта (для данного проекта). Эту часть БД САПР назовём объектной частью базы данных (ОЧ БД).

В проектной или конструкторской организации в работе может на­ходиться од­­но­временно несколько проектов. Для каждого проекта соз­­­даётся своя часть ба­­зы данных (ОЧ₁ БД, ОЧ₂ БД, …).Срок дей­ствия ОЧ_i БД определяется продол­жительностью выполнения работ по i-му проекту.

При начале проектирования i-го объекта в ОЧ_i БД переписыва­ется из систем­ной части базы данных (СЧ БД) информация, необхо­ди­­мая для выполнения про­екта (данные по комплектующим деталям, типо­вым решениям, данные по аналогам и т.д.). В дальнейшем в ре­зуль­та­те решения проектных задач по i-му объекту осуществляется по­пол­­­не­ние ОЧ_i БД. Схема формирова­ния объектной части базы дан­ных для i-го проекта показана на рис.9.3.

На рис.9.3:

1 – системная часть базы данных;

2 – задание на проектирование (ТЗ);

3 – процедура начального формирования объектной части БД;

4 – объектная часть БД (начальное состояние);

5 – подсистемы проектирования объекта;

6 – промежуточные и окончательные результаты решения проектных задач;

Рис.9.3. Схема формирования объектной части базы

данных для i-го проекта

7 – процедуры пополнения объектной части БД;

8 – объектная часть БД (текущее состояние) – наполнение промежуточными и конечными результатами.

К базе данных САПР предъявляются следующие основные требования:

1. Универсальность, т.е. наличие в БД всей необходи­мой инфор­мации и возможность доступа к ней при решении проектных задач.

2. Открытость БД для внесения в неё новой информации и кор­ректиров­ки имеющейся.

3. Секретность – невозможность несанкционированного доступа к ин­фор­­мации и её изменение.

4. Оптимизация организации базы данных САПР, заключаю­щаяся в ми­ни­­ми­зации избыточности данных.

5. Целостность данных, т.е. их непротиворечивость и досто­вер­ность.

6. Восстанавливаемость – возможность восстановления БД пос-­

ле сбоя сис­темы или отдельных видов порчи системы. В ос­ -

новном свойство восстанавливаемости обеспечивается дуб-­

лиро­ванием БД и исполь­зованием аппаратных средств повы-­

шен­­­­­ной надёжности.

7.Эффективность – минимальное время реакции на запрос поль­­­-

зователя (программы или проектировщика) и минималь­ные

потребности в па­мяти.

Создание БД САПР, поддержка её в целостном, непротиворе­чи­вом состоя­нии, обеспечение безопасности её использования и сохран­ности информации вплоть до восстановления её после различных сбо­­ев, предоставление данных поль­зователям (прикладным програм­мам и проектировщикам) обеспечивается выбранной и применённой системой управления базой данных (СУБД).

При разработке БД САПР должны быть определены:

- объекты;

- атрибуты и их значения;

- связи между объектами.

Анализ состава данных, подлежащих включению в базу данных, т.е. определение состава объектов, атрибутов и их значений, начина­ют с изучения будущих запросов со стороны прикладных программ и проектировщиков.

Кроме того, при разработке БД САПР необходимо провести сис­те­матиза­цию свойств и особенностей информации, которая должна использоваться при проектировании или конструировании объектов определённого вида.

Систематизация должна привести к классификации данных.

В качестве примера приведём один из возможных вариантов ис­следования свойств данных, причём, только для нормативно-справоч­ной информации.

Таблица 9.1

Классификация свойств и состава проектных данных

Признак классификации	Свойства и состав проектных данных
Масштаб применения	Системные (многоразовые), объектные
Время действия	Условно-постоянные, переменные
Назначение сведений	Исходные, промежуточные, выходные
Форма представления	Текстовые, табличные, цифровые, гра­фические
Вид информационных документов	Организационные, методические, нор­мативные, справочные
Предметная принад­- леж­­ность	Строительство, теплоснабжение, элек­троснабжение и т.д.
Вид ресурсов	Сырьё, материалы, оборудование и др.

Классификационные признаки позволяют описывать данные в различных аспектах. Приведём в качестве примера состав файлов для следующих призна­ков классификации:

- предметная принадлежность (например, БД технологического раздела по рис. 9.4);

- ресурсы.

Рис.9.4. Состав файлов базы данных САПР «Технологический раздел»

На рис. 9.4:

1 – файлы технологических процессов (сварка, шлифование, фре­зерование и т.д.);

2 – файлы оборудования и приборов (станок типа А, станок типа Б и т.д.);

3 – файлы ресурсов (трудоёмкость, сырьё, материалы, инстру­мент, энергоресурсы и т.д.);

4 – нормативные файлы (расходы электроэнергии, расходы сы­рья, расходы материалов и т.д.).

Внутри БД САПР файлы связаны между собой. Например, в при­ведённом примере файлы «Оборудование и приборы» связаны с фай­лами «Ресурсы» и «Нормативы». Поэтому в структуре файлов дол­жны использоваться адреса связей.

Анализ связей должен быть очень тщательным, так как должны быть предусмотрены связи как между файлами раздела базы, так и связи между её разделами.

Для отражения связей используют главные и связующие файлы. Посредством организации цепочек связей БД САПР формирует пол­ный состав выдаваемых данных.

Один и тот же файл может принадлежать различным подмно­же­ствам БД САПР. В этом случае принадлежность файла к тем или иным подмножествам определяется через адреса связей. Фрагмент ва­рианта взаимосвязи файлов показан на рис.9.5.

На рис. 9.5:

1 – файл «Оборудование»;

2 – файл «Режимы работы; временные характеристики»;

3 – файл «Загрязнение окружающей среды»;

4 – файл «Габаритные размеры, масса, вибрация»;

Подмножество А базы данных – «Проектирование вентиляции»;

Подмножество Б базы данных – «Строительное проектирование».

Важное значение имеет словарь данных (интегрированный сис­тем­­ный каталог), являющийся хранилищем информации, описываю­щей данные базы данных.

В словаре данных должна содержаться следующая информация:

- имена, типы и размеры элементов данных;

- имена связей;

- имена пользователей, которым предоставлено право доступа к данным;

- форматы представления данных.

Рис.9.5. Фрагмент взаимосвязей файлов в базе данных САПР

База данных САПР является фундаментальным компонентом сис­темы автоматизированного проектирования. Поэтому разработка БД САПР является важнейшей частью работы по созданию системы ав­томатизированного проектирования.

Рис.9.6. Схема разработки базы данных САПР

На рис.9.6 показана схема процесса разработки базы данных САПР.

На рис.9.6:

1 – планирование разработки базы данных БД САПР;

2 – определение требований к БД САПР;

3 – анализ требований;

4 – концептуальное проектирование БД САПР;

5- учёт требований выбранной СУБД;

6 – логическое проектирование БД САПР;

7 – физическое проектирование БД САПР;

8 – анализ и оценка полученных результатов;

9 – реализация БД САПР.

9.2. Методическое и организационное обеспечение САПР

САПР представляет собой не только совокупность технических, ма­темати­ческих, программных, информационных, языковых компо­нентов, но и объеди­ня­ет эти компоненты с коллективами проекти­ров­щиков и конструкторов, уча­ствующих в процессах автоматизирован­ного проектирования. Иными словами, САПР - организационно-тех­ническая система. Поэтому важными компонен­та­ми САПР являются методическое и организационное обеспечение.

Методическое обеспечение представляет собой набор докумен­тов, в кото­рых описывается организация работ по разработке САПР; определяются задачи проектирования, подлежащие автоматизации фор­мулируются требования к тех­ническому, математическому, ин­фор­мационному обеспечению системы; при­водятся характеристики компонентов системы; правила и рекомендации по от­ладке и испыта­ниям системы.

В состав методических материалов входят должностные инструк­ции об­слу­живающего персонала, рекомендации по устранению неис­правностей и от­казов, формы эксплуатационной документации, реко­мендации по профилак­ти­ческим работам.

Организационное обеспечение представляет собой совокуп­ность докуме­н­тов, характеризующих состав проектной или конструк­тор­ской организации; взаимодействие подразделений этой организа­ции (отделов, лабораторий, секто­ров, групп) при выполнении проект­ной или конструкторской работы; виды ра­бот, выполняемых система­ми автоматизированного проектирования; организа­цию контроля за хо­дом разработки технической документации и за получае­мыми ре­зуль­татами.

Отличительной чертой любого процесса проектирования являет­ся его не­определённость, которая устраняется в результате итераци­он­­ных циклов про­ек­тирования заданного объекта.

Неопределённость исходных данных, ограничений, критериев, це­­лей в за­даче проектирования вызывает необходимость контроля за текущим состоя­ни­ем процесса автоматизированного проектирования и обмена проектными реше­ниями между блоками системы проекти­ро­­вания (между проектировщиками, секторами и отделами проектной организации).

В проектной (конструкторской) организации должна быть разра­бо­тана струк­турная технологическая схема, в которой указываются все проектные бло­ки и взаимосвязи между ними. А по каждому про­ектному блоку должны быть разработаны структурные схемы взаи­мо­связи проектных решений.

Могут использоваться следующие типовые структурные схемы процесса автоматизированного проектирования (рис.9.7):

а) - последовательная;

б) - параллельная;

в) - итерационная;

г) - последовательно-параллельная.

В результате анализа проектных решений, операций и процедур разрабатывают структурную схему, которая отображает технологию автоматизированного проектирования объектов определённого клас-­ са. Как правило, в такой схеме используются все типовые структур­ные схемы, показанные на рис.9.7.

9.3. Автоматизированное проектирование систем автома­ти­чес­ко­го уп­­­­равления

Системы автоматического управления (САУ) широко ис­пользу­ются в различных областях производства для управления тех­­­нологи­ческими процессами, установками, аппаратами и механизма­ми. С по­мощью САУ осуществляется как программное изменение значений

Рис.9.7. Типовые структурные схемы процесса автоматизированного

проектирования

технологических параметров, так и поддержание значений парамет­ров на заданных уровнях. ­Рассмотрим этапы работы, выполняемые при автоматизирован­ном проектировании системы автоматического управления (рис.9.8).

На рис.9.8:

1 – изучение требований ТЗ; ознакомление со свойствами, особенностями, характеристиками управляемого объекта;

2 – выбор структуры системы управления (структурный синтез);

3 – анализ решений по структуре системы;

4,7,9 – проверка решений на соответствие требованиям техни­чес­кого задания;

5 – выбор параметров системы (параметрический синтез);

6 – компьютерное моделирование проектируемой АСУ;

7,8,9 – выбор аппаратных и программных средств для реализации АСУ;

10 – определение характеристик САУ (надёжность, устойчивость, точность, стоимость и т.д.);

11 – оформление документации

Рис.9.8. Этапы работы при автоматизированном проектировании систем

автоматического управления

При автоматизированном проектировании систем САУ разраба­ты­ваются функциональная, структурная и прин­­­­­­­­­ци­пиальная схемы. Определяются парамет­ры системы, вы­би­­раются аппаратные и прог­раммные средства системы.

9.4. Автоматизированное проектирование АСУТП (автомати­зированных систем управления технологическими процессами)

При проектировании АСУТП наибольшие трудности связаны с вы­бором структуры систе­мы, информационных, функциональных и логи­чес­ких связей между элементами и устройствами системы управ­ления.

При проектировании системы управления необходимо учиты­вать, что объект управления или уже существует, или проектируется заранее и даже другими организациями. В связи с этим большинство свойств и характеристик объекта управления уже не подлежит изме­нению.

В перспективе желательно, чтобы объект управления и управ­ля­ю­­­щая им система проектировались одновременно и комплексно. В этом случае будет создан более эффективный автоматический или ав­томатизированный комплекс, представляющий собой взаимосвя­зан­ное объединение объекта управления и системы управления.

Необходимо учитывать, что математические модели при проекти­ровании разрабатывают в условиях существенно неполной информа­ции об объекте управления, о возмущениях, которые будут на него дей­ствовать. Кроме того, недостаточно полной может быть и инфор­ма­­ция, которая будет поступать в систему управления от объекта. По­мимо всего прочего, при функционировании на систему управле­ния могут оказывать воздействие случайные помехи.

Важнейшим условием работоспособности систем автоматичес­ко­го и автоматизированного управления является устойчивость. Поэто­му в состав САПР должна входить процедура проверки проектируе­мой системы на устойчивость.

Как правило, автоматизированные системы управления сложны­ми технологическими комплексами имеют многоуровневую иерархи­ческую структуру (рис.9.9).

Структура АСУТП состоит из следующей последовательности уровней:

- управляемого технологического процесса, представляющего со­бой совокупность взаимосвязанных аппаратов и установок (А₁,А₂, …А_n) – объектов управления;

Рис.9.9. Иерархическая структура АСУТП сложным

технологическим комплексом

- уровня систем автоматического управления (САУ₁,САУ₂,… САУ_n), стабилизирующих или изменяющих режим протекания про­цессов в аппаратах и установках А₁, А₂,…А_n в соответствии с задаю­щими воздействиями, поступающими от уровня управления;

- уровня управления (оптимизации), состоящего из управляю­щих устройств С₁,С₂,…С_n, вырабатывающих значения уставок систе­мам САУ₁, САУ₂,…САУ_n на основе локальных критериев управления объ­ектами А₁,А₂,…,А_n;

- уровня координации, координирующего (подчиняющего) ло­каль­ные цели управления объектами управления А₁,А₂,…А_n глобаль­ной цели управления всем технологическим процессом в целом.

При автоматизированном проектировании АСУТП должны быть решены следующие основные задачи:

- определена структура системы;

- выбраны законы автоматического регулирования и управления (второй уровень системы);

- выбраны методы оптимального управления, предназначенные для применения на третьем уровне системы;

- выбраны методы теории координированного управления, пред­назначенные для применения на четвёртом уровне системы;

- разработаны алгоритмы и программы реализации выбранных методов обработки информации и управления;

- выбраны аппаратные средства системы (датчики, исполнитель­ные механизмы объектов управления, микропроцессоры, преобразо­ватели сигналов, компьютеры и др.).

САПР автоматизированных систем управления должны предус­матривать возможности исследования вопроса о рациональном рас­пределении функций между человеком и средствами вычислительной техники в процессе эксплуатации системы. Должны быть определены режимы интерактивного взаимодействия между операторами и компьютерами так, чтобы обеспечить не только требуемое качество и точность регулирования и управления, но и выполнение других тре­бо­ваний, предъявляемых к системе управления (экономические пока­затели, надёжность и т.д.).

Заключение

Определены понятия информационного обеспечения и базы данных САПР, сформулированы требования к ним для нормального функционирования системы. БД САПР является основным связую­щим звеном между отдельными проектными процедурами, операция­ми, задачами. Формирование, загрузка и корректировка справочной информации осуществляется исключительно администратором базы данных. База данных САПР является фундаментальным компонентом сис­темы автоматизированного проектирования. Поэтому разработка БД САПР является важнейшей частью работы по созданию системы.

Методическое обеспечение представляет собой набор докумен­тов, в кото­рых описывается организация работ по разработке САПР; определяются задачи проектирования, подлежащие автоматизации, фор­мулируются требования к тех­ническому, математическому, ин­фор­мационному обеспечению системы. Организационное обеспече­ние представляет собой совокуп­ность докуме­н­тов, характеризующих состав проектной или конструк­тор­ской организации; взаимодействие подразделений организа­ции при выполнении проект­ной или кон­­ст­рук­торской работы; виды ра­бот, выполняемых система­ми автомати­зированного проектирования; организа­цию контроля за хо­дом раз- ботки технической документации и за получае­мыми ре­зуль­татами.

­Определены этапы работы, выполняемые при автоматизирован­ном проектировании системы автоматического управления, призван­ных осуществлять как программное изменение значений технологи­ческих параметров, так и поддержание значений парамет­ров на задан­ных уровнях.

При проектировании АСУТП наибольшие трудности связаны с вы­­бором структуры систе­мы, информационных, функциональных и логи­чес­ких связей между элементами и устройствами системы управ­ления. Математические модели при проекти­ровании разрабатывают в условиях неполной информа­ции об объекте управления, о возмуще­ни­­­ях, которые будут на него дей­ствовать; недостаточно полной мо­жет быть и инфор­ма­­ция, которая будет поступать в систему управле­ния от объекта. Как правило, автоматизированные системы управле­ния сложны­ми технологическими комплексами имеют многоуров­не­вую иерархи­ческую структуру.

Вопросы для самопроверки

1. Что понимают под термином «Информационное обеспечение САПАР»?

2. Какие функции выполняет база данных САПР?

3. Как классифицируется информация, образующая информационное обеспечение САПР?

4. Приведите схему информационных потоков САПР.

5. Схема формирования и функции объектной части базы данных САПР.

6. Требования, предъявляемые к базе данных САПР.

7. Расскажите об этапах разработки базы данных САПР.

8. Что представляет собой методическое обеспечение САПР?

9. Что представляет собой организационное обеспечение САПР?

10. Из каких этапов состоит автоматизированное проектирование систем автоматического управления?

11. Какую структуру имеет АСУТП сложным технологическим комплек­сом?

12. Основные задачи, которые должны быть решены при автоматизирован­ном проектировании АСУТП.

Выводы

Учебное пособие «Системы автоматизации проектных работ: курс лекций» написано по материалам лекций, которые авторы чита­ют много лет студентам специальности «Вычислительные машины, комп­лексы, системы и сети» на ФАИТ и заочном факультете Самар­ского государственного технического универси­тета. Кроме того, ав­торы ведут лабораторные работы по данной дисциплине.

Естественно, курс лекций в процессе работы над рукописью был существенно переработан.

В учебном пособии приводятся общие сведения о проектиро­ва­нии и конструировании. Поясняется – в чём разница между проект­ными и конструкторскими работами. Перечисляются недостатки неавтоматизированной технологии проектирования.

При переходе к автоматизированному проектированию в органи­за­ции должна создаваться технология автоматизированного проекти­рования.

Наиболее важными целями перехода к автоматизированному про­­­­­ек­ти­рованию являются: сокращение затрат времени на разработку проекта; увеличение числа проектов, выпускаемых проектной орга­ни­­­­­зацией; повышение качества проектной документации; возмож­ность решения оптимизационных задач.

Даны четыре взаимодополняющие определения понятия САПР. Од­­но из определений САПР – это взаимосвязанная совокупность ря­да компонентов. Компоненты САПР (состав САПР): техническое об­ес­печение, математическое обеспечение, программное обеспе­че­ние, информационное обеспечение, лингвистическое обеспечение, мето­ди­­ческое обеспечение, организационное обеспечение.

Приведена классификация САПР по различным признакам.

Важной компонентой САПР является её техническое обеспе­че­ние. Рассмотрена структура технического обеспечения САПР и тре­бования к используемым аппаратным средствам САПР.

Поясняется, что такое программное обеспечение САПР и из ка­ких частей оно состоит.

Математическое обеспечение является важнейшей компонентой САПР. В состав математического обеспечения входят математи­чес­кие модели проектируемых объектов, систем, процессов; численные методы решения математических задач, алгоритмы выполнения про­ектных процедур.

Даны определения понятию «математическая модель проекти­руе­мого объекта», перечислены требования к математичес­ким моделям САПР, рассмотрены этапы построения математических моделей САПР. В некоторых случаях математическую модель проектируемого объекта можно представить в виде чёрного ящика.

Подробно рассмотрена классификация математических моделей, которая может оказаться полезной при разработке математического обеспечения проектируемой САПР.

Процедуры синтеза в САПР представлены в виде последо­ва­тель­ности ряда задач: разработка функциональной схемы, опреде­ле­ние состава объекта, структурный синтез (разработка или выбор струк­туры объекта), параметрический синтез, проектирование кон­струкции объекта.

Подробно рассмотрена задача размещения. Задача размещения весьма универсальна и широко используется для решения задач раз­мещения станочного и другого производственного оборудования, энергетических узлов, узлов связи и т.д.

Рассмотрена задача размещения на печатной плате радиоэлек­трон­ных элементов. Приведены формулировка задачи и целевая функ­ция, которая должна быть минимизирована.

Следующая после синтеза группа проектных процедур – про­це­ду­ры анализа. Отмечено, что анализ объектов при автома­тизиро­ван­ном проектировании основан на математическом моделировании, т.е. на исследовании проектируемых объектов, систем, процессов путём оперирования их математическими моделями.

Обращено внимание на то, что при создании САПР усилия дол­жны быть направлены не только на разработку математических моде­лей проектируемых объектов, систем, процессов, но и на развитие чис­­ленных методов решения задач и алгоритмов анализа получаемых проектных решений.

Большое внимание было уделено вопросам оптимизации. Задача оптимизации при автоматизированном проектировании возникает в связи с необходимостью выбора наилучших вариантов конструкции аппаратов, станков, машин, механизмов; параметров схем и проек­ти­руемых устройств, режимов работы оборудования и т.д.

Приведены примеры проектных оптимизационных задач: проек­ти­рование контроллера для автоматической системы управления, про­­ектирование магистрального нефтепровода, проектирование ма­гис­­трального газопровода, проектирование высоковольтной ЛЭП.

Показана необходимость при разработке САПР получение зави­си­мости численного критерия оптимальности от внешних и внут­рен­них параметров проектируемого объекта, системы, процесса и от эле­ментов решения оптимизационной задачи.

При решении оптимизационной задачи важное значение имеет критерий оптимальности.

Во многих случаях проектируемый объект характеризуется нес­коль­­кими показателями качества. Оптимизационные задачи с нес­коль­кими критериями качества называются многокритериальными. Рассмотрены методы решения оптимизационной задачи при нес­коль­ких показателях качества.

Рассмотрены подходы к решению задач синтеза объекта, систе­мы, процесса. Рассмотрены вопросы структурного и парамет­ричес­ко­го синтеза. Подчёркнуто, что для структурного синтеза объектов, сис­тем, процессов расширяется применение интеллек­туальных сис­тем.

Все САПР выполняют как процедуры синтеза проектных реше­ний, так и процедуры анализа.

К математическому обеспечению анализа относятся математичес­кие модели анализа проектных решений, численные методы и алго­ритмы выполнения проектных процедур анализа. В пособии рассмот­рены этапы разработки математической моде­ли анализа проектных решений.

Рассмотрены вопросы построения математических моделей ана­ли­за проектных решений для различных иерархических уровней объ­екта, системы, процесса.

Для многих объектов, систем, процессов анализ проектных реше­ний на системном уровне связан с исследованием прохождения через объект, систему, процесс потока заявок (требований). Подробно рас­смотрено применение в качестве математического аппарата моде­ли­рования теории массового обслуживания.

Подсистемы машинной графики и геометрического модели­ро­ва­ния входят в состав многих САПР. В пособии приведены сведения по двумерным системам (2D) и по программному пакету КОМПАС-3D. Описано, какие задачи могут быть решены при помощи графического редактора AutoCAD и при помощи программ КОМПАС-3D.

Важнейшим компонентом любой САПР является её информа­ционное обеспечение. В пособии даны определения понятий «Инфор­мационное обеспечение САПР», «База данных САПР». Показана схе­ма информационных потоков САПР, приведён перечень требова­ний к базам данных САПР. Определена последовательность этапов разра­бот­ки базы данных САПР.

САПР – организационно-техническая система. Поэтому важными компонентами любой САПР являются её организационное и методи­чес­кое обеспечение. Рассмотрены типовые структурные схемы про­цес­­­са автоматизированного проектирования.

В качестве примера рассмотрены этапы работ, выполняемые при автоматизированном проектировании систем автоматического и авто­ма­­тизированного управления.

Данное учебное пособие ориентировано на подготовку в области САПР студентов специальности «Вычислительные машины, компле­ксы, системы и сети».

Заключение

В XX1 веке специалистам (обществу) придётся решать ряд слож­ных проблем, связанных с экологией, с поиском новых источников энергии, материалов, технологий. Ещё более актуальными станут проблемы обеспечения населения земли продовольствием и питьевой водой. Определяющая роль в решении названных проблем отводится информационным технологиям.

Среди информационных технологий автоматизация проектиро­ва­ния занимает особое место.

Во-первых, автоматизация проектирования – комплексная дис­цип­­лина, её составными частями являются многие другие дисципли­ны (прикладная математика, теория оптимизации, машинная графика и др.) и информационные технологии. Так, техническое обеспечение систем автоматизированного проектирования (САПР) основано на использовании вычислительных сетей и телекоммуникационных тех­нологий, в САПР используются современные компьютеры и перифе­рийное оборудование.

В состав математического обоснования САПР входят математи­чес­кие модели проектируемых систем, объектов, процессов. Широко используются методы оптимизации, дискретной математики, статис­тики.

Программные комплексы САПР относятся к числу наиболее слож­­ных программных систем. При разработке САПР используются самые современные языки программирования.

Характеристики САПР существенно зависят от её информацион­ного обеспечения, разработке которого при создании САПР должно быть уделено серьёзное внимание.

Во-вторых, знание основ автоматизации проектирования, умение разрабатывать новые САПР, совершенствовать существующие систе­мы САПР и поддерживать их в эксплуатации требуется практически любому инженеру специальности «Вычислительные машины, комп­лексы, системы и сети».

Предприятия, ведущие разработки новых изделий с малой степе­нью использования САПР, оказываются неконкурентоспособными вследствие больших временных и материальных затрат как на проек­тирование объектов, так и ввиду невысокого качества выпускаемых проектов.

Библиографический список

1. Антонов А.В. Системный анализ. Учебник для вузов. – М.: Выс­шая школа, 2006. -454 с.

2. Новосельцев В.И., Тарасов Б.В., Голиков В.К., Дёмин Б.Б. Тео­ре­тические основы системного анализа. М.: Изд-во «Майор»+, 2006.- 592 с.

3. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им Баумана Н.Э., 2002. – 336 с.

4. Кондаков А.И. САПР технологических процессов: учебник для студентов высших учебных заведений / А.И. Кондаков. – М.: Изда­тельский центр «Академия», 2007. – 272 с.

5. Черепашков А.А., Носов Н.В. Компьютерные технологии, моде­ли­рование и автоматизирован­ные системы в машиностроении: учеб­­ное пособие для ВПО. Волгоград, ИД «Ин-Фолио», 2009. – 640 с.

6. Соколова Т.Ю. AutoCAD 2011. Учебный курс (+CD). Изд-во «Питер», 2011.-576 с.

7. Кидрук М. Компас 3D, V10. М.: Изд-во «Питер», 2009. -555 с.

8. Кун Ву Ли. Основы САПР. – СПб.: Изд-во «Питер», 2004. – 560 с.

9. Жук Д.М. и др. Технические средства и операционные системы САПР. / Д.М. Жук, В.А. Мартынюк, П.А. Сомов.– Минск: «Высшая школа», 1988.- 155 с.

135