Санкт-Петербургский государственный электротехнический университет

“ЛЭТИ”

ОТЧЕТ

по лабораторно-практической работе № 5

Исследование свойств конденсаторных материалов

Выполнил Демьянов Н.В.

Факультет ФЭЛ

Группа № 3203

Преподаватель

“Выполнено” “____” ___________

Подпись преподавателя __________

6. ИССЛЕДОВАНИЕ СВОЙСТВ КОНДЕНСАТОРНЫХ МАТЕРИАЛОВ

6 1 Основные понятия и определения

Конденсаторные материалы применяются в качестве рабочего диэлектрика в конденсаторах. К основным параметрам конденсатора относят емкость С, температурный коэффициент емкости α_с, тангенс угла диэлектрических потерь tgδ. Значения этих параметров во многом обусловлены свойствами используемого диэлектрического материала.

Емкость конденсатора С определяется как отношение накопленного в нем заряда Q к напряжению U, приложенному к электродам, и зависит от конструкции и геометрических размеров конденсатора, а также от диэлектрической проницаемости диэлектрика. Емкость простейшего плоского конденсатора с электродами, имеющими форму квадрата, определяется выражением:

, (6.1)

где ε₀ = 8,85-10^-12 Ф/м - электрическая постоянная; ε - относительная диэлектрическая проницаемость диэлектрика; l – сторона квадрата, h - толщина диэлектрика. Как следует из выражения (6.1), для увеличения емкости конденсатора при минимальных его размерах и прочих равных условиях необходимо применять материалы с возможно большим значением диэлектрической проницаемости.

Температурный коэффициент емкости α_C отражает отклонение емкости, обусловленное изменением температуры и, следовательно, характеризует температурную стабильность емкости конденсатора. Общее определение этого параметра соответствует выражению:

α_C= (1/C)·(dC/dt) (6.2)

Дифференцирование выражения (6.1) дает:

dC/dt = ε₀ [ (l²/h)·(dε/dt) + (2εl/h)·(dl/dt) – (εl²/h²)·(dh/dt) ] (6.3)

Разделив левую и правую части выражения (6.3) на левую и правую части выражения (2.1), получим:

(1/C)·(dC/dt) = (1/ε)·(dε/dt) + (2/l)·(dl/dt) – (1/h)·(dh/dt)

или

α_C = α_ε + 2α_Μ –α_Д,

где α_С , α_М и α_Д - температурные коэффициенты диэлектрической проницаемости диэлектрика, линейного расширения металла электродов и линейного расширения диэлектрика соответственно.

В металлизированных конденсаторах, где в качестве электродов используется тонкий слой металла, нанесенный непосредственно на твердый диэлектрик, изменение размеров электродов будет определяться расширением диэлектрика, а не металла. В этом случае можно считать α_М = α_Д, и температурный коэффициент емкости будет:

α_С = α_ε + α_Д . (6.4)

Поскольку значение емкости определяется суммой различных механизмов поляризации диэлектрика, температурная зависимость емкости может иметь различный характер, а параметр α_С может быть положительным, отрицательным и близким к нулю.

При включении конденсатора под напряжение в нем наблюдаются потери электрической энергии, приводящие к его нагреванию. Потери энергии складываются из потерь в диэлектрике и потерь в проводящих частях конденсатора. Для описания потерь на переменном напряжении обычно используют тангенс угла потерь tgδ, где δ - угол, дополняющий до 90^о угол сдвига фаз между действующим на конденсаторе напряжением и проходящим через него током. Параметр tgδ характеризует склонность конденсатора рассеивать энергию и, в конечном счете, определяет возможность использования конденсатора в заданном диапазоне частот.

Различают высокочастотные и низкочастотные конденсаторные материалы. В качестве высокочастотных применяются неполярные полимеры, ионные диэлектрики с плотной упаковкой ионов. В них на высоких частотах главную роль играет электронная или ионная поляризация; потери энергии обусловлены в основном электропроводностью. Такие материалы имеют малые значения tgδ, который растет при увеличении температуры по экспоненциальному закону. К низкочастотным материалам относятся полярные полимеры, диэлектрики с сегнетоэлектрическими свойствами. В области низких частот в них преобладают замедленные механизмы поляризации; потери энергии носят релаксационный характер. Материалы этой группы характеризуются повышенным tgδ, но обладают весьма высокой диэлектрической проницаемостью, что позволяет изготавливать на их основе конденсаторы большой емкости с малыми габаритами.

В настоящей работе измеряются параметры металлизированных конденсаторов, в которых в качестве рабочего диэлектрика используются исследуемые материалы.

6.2. Описание установки

Испытательная установка состоит из пульта и цифрового моста, измеряющего емкость и tgδ. В пульте находится термостат, температура в котором может изменяться регулятором УСТАНОВКА ТЕМПЕРАТУРЫ . Температура в термостате измеряется с помощью термопары, подключенной к расположенному на пульте прибору, проградуированному в градусах Цельсия.

В термостате размещены конденсаторы С1...C5, рабочими диэлектриками в которых являются исследуемые материалы (их наименования указаны на пульте). Термостат имеет выводы “С”, расположенные на панели пульта и предназначенные для соединения с измерителем емкости. Используемые конденсаторы поочередно могут быть подключены к этим выводам с помощью переключателя. В положении переключателя “С₀” измеряется емкость проводников, соединяющих образцы в термостате с прибором.

В качестве измерителя емкости может быть применен любой прибор, позволяющий измерять емкость с точностью до десятых долей пикофарады. Часто такие приборы позволяют измерять не только емкости образцов, но и потери в них, характеризуемые значениями tgδ. В данной работе использован цифровой мост, предназначенный для измерения емкости и tgδ на определенной фиксированной частоте.

Исходные данные

С₀ = 16,3 пф

Температурные коэффициенты линейного расширения диэлектриков

Неорганическое стекло 3*10^-6 К

Слюда 13,5*10^-6 К

Тиконд 8*10^-6 К

Полипропилен 1,1*10^-4 К

Сегнетокерамика 12*10^-6 К

Справочные значения tg δ на частоте 1 МГц

Материал	tg δ
Слюда	(1…6)*10-4
Щелочные силикатные стекла	(2…7)*10-3
Тиконд	не найден
Полипропилен	(3…5)*10-4
Сегнетокерамика	0,05…0,3

Обработка результатов.

1. Графики зависимости С(Т)

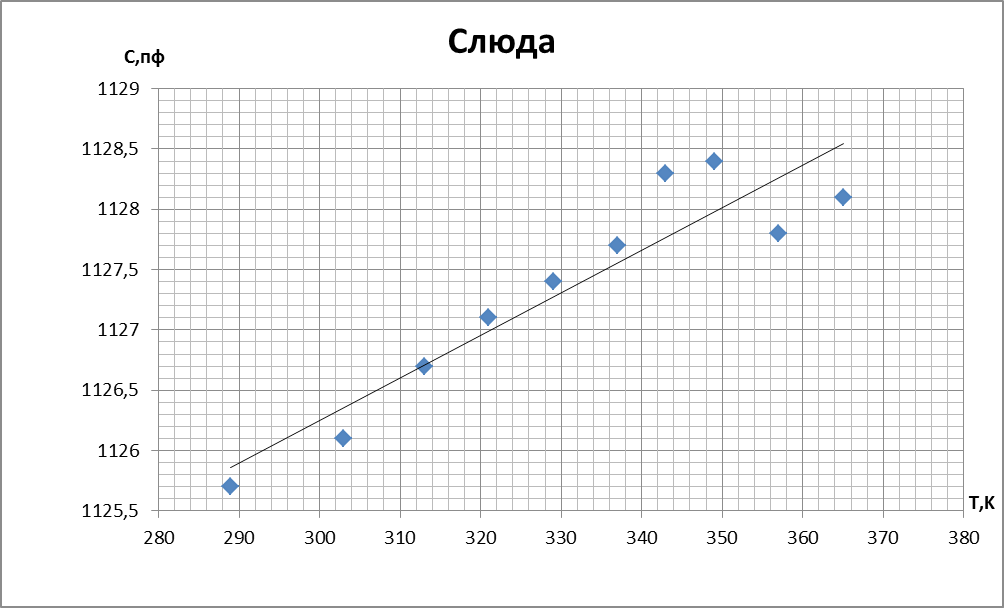
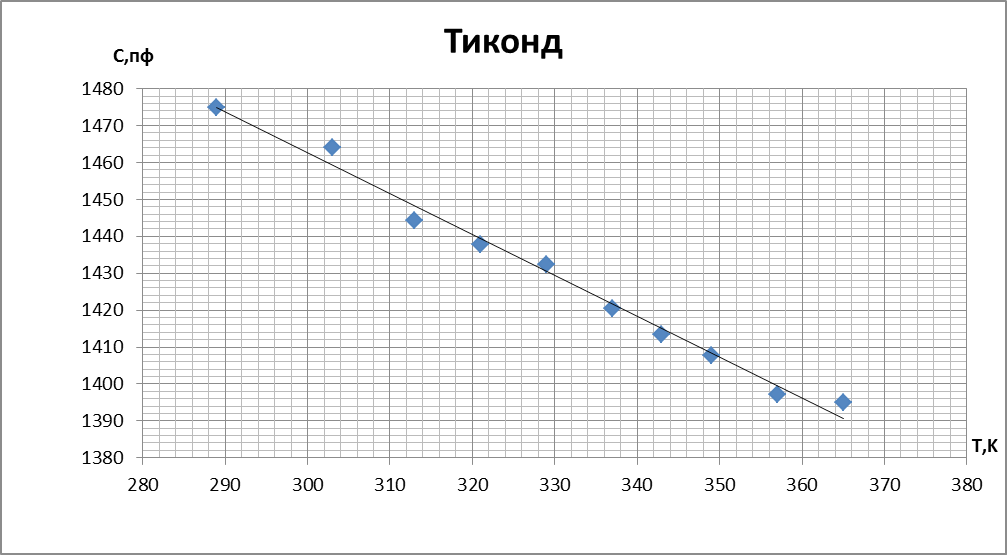
2. Графики температурной зависимости tg δ

3. Нахождение температурного коэффициента емкости

Расчет проводится по формуле:

Для расчета α_с нужно вычислить производную dС/dT. Она рассчитана в MS Excel с помощью функции ЛИНЕЙН() (аппроксимация исходных данных линейной зависимостью y = k*x+b, производная dС/dT при данной температуре равна коэффициенту k).

Результаты расчета:

4. Нахождение температурного коэффициента диэлектрической проницаемости

Так как в работе исследуются параметры именно металлизированных конденсаторов, изменение размеров электродов будет определяться линейным расширением диэлектрика, а не металла, поэтому справедлива формула:

где α_d – коэффициент линейного расширения диэлектрика.

Результаты расчета:

5. Графики температурной зависимости α_ε

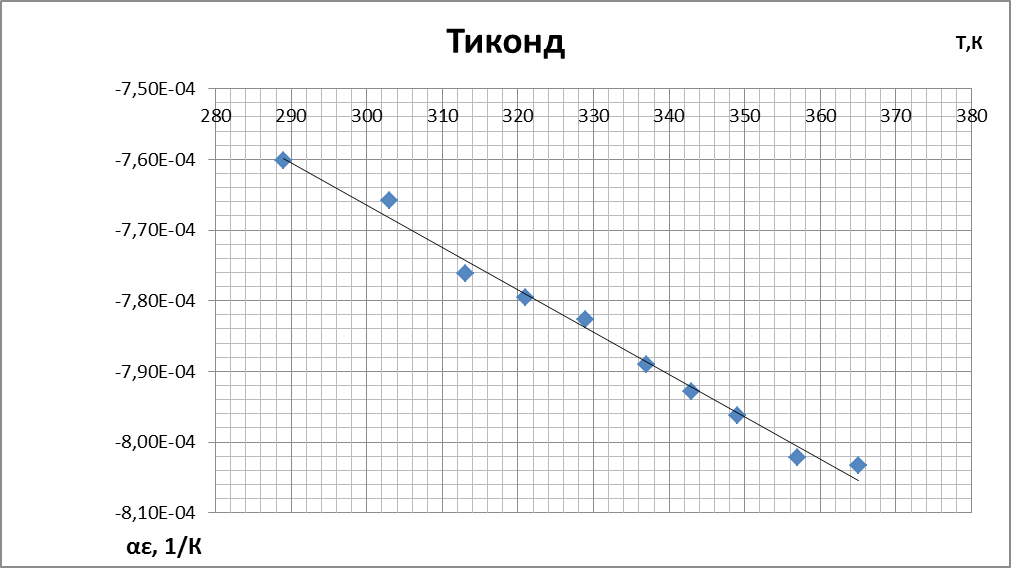
Вывод: У слюдяного конденсатора и у конденсатора с диэлектриком из органического стекла ёмкость с увеличением температуры растёт. У конденсатора с полипропиленовым диэлектриком и с диэлектриком из тиконда ёмкость уменьшается с ростом температуры. Наиболее интересные явления наблюдаются у сегнетокерамики, ёмкость такого конденсатора растёт до некоторой температуры (60°C), далее уменьшается т.к. уменьшается диэлектрическая проницаемость сегнетоэлектрика. Это связанно с исчезновением спонтанной поляризации в сегнетоэлектрике после достижения точки Кюри.