Обработка результатов измерений

1.1. Расчет удельного сопротивления металлических проводников

Расчет проводим по формуле

ρ = RS/l,

где R – сопротивление образца, S – площадь его поперечного сечения,

l – длина проводника.

Результаты расчета сведены в таблицу:

Материал	R, Ом	l, мм	D, мм	ρ, мкОм*м	ρ(справ.), мкОм*м
Манганин	106,1	1530	0,1	0,5446454	не найдено
Медь	12,90	11600	0,13	0,0147607	0,0168
Нихром	2,5	1000	0,7	0,9621128	не найдено
Константан	253,3	1300	0,06	0,5509145	не найдено
Никель	2,3	1700	0,25	0,0664123	0,068

Примечание В справочных данных указано значение удельного сопротивления

меди и никеля при 20°С.

1.2. Расчет сопротивления квадрата поверхности металлических пленок

Для расчета используем формулу

R_▫ = Rb/l,

где R – сопротивление образца, b – ширина резистивного слоя,

l – длина пленки (расстояние между контактными площадками)

Результаты вычислений сведены в таблицу:

Материал	R, Ом	b, мм	l, мм	R▫, Ом
R1	42,7	2,5	0,2	533,75
R2	804,70	2	3,25	495,2
R3	7895	0,6	9,5	498,63158

2.1. Таблица зависимости сопротивления проводников от температуры

В этой таблице приводятся результаты опыта:

Медь		Никель		Константан
t, ˚C	Rt, Ом	t, ˚C	Rt, Ом	t, ˚C	Rt, Ом
27	64,8	27	22,3	27	26,9
54	72	54	27	54	29,4
68	74,2	68	28,4	68	29,4
80	76,6	80	30,3	80	29,4
95	78	95	30,8	95	29,2
115	81,5	115	32,4	115	29,2
150	86,8	150	35,3	150	29,2
190	90,7	190	37,6	190	28,5

2.2. Графики зависимости сопротивления проводников от температуры

3. Расчет температурного коэффициента удельного сопротивления

Для расчета α_ρ нужно вычислить производную dR/dT. Она рассчитана в MS Excel с помощью функции ЛИНЕЙН() (аппроксимация исходных данных линейной зависимостью y = k*x+b, производная dR/dT равна коэффициенту k).

Значения dR/dT:

Для меди 0,153 Ом/К;

Для никеля 0,088 Ом/К;

Для константана 0,004 Ом/К.

Далее вычисляются значения α_ρ, результаты вычислений занесены в таблицу:

Медь			Никель			Константан
t, ˚C	Rt, Ом	αρ, K-1	t, ˚C	Rt, Ом	αρ, K-1	t, ˚C	Rt, Ом	αρ, K-1
27	64,8	0,002378	27	22,3	0,003974	27	26,9	0,000166
54	72	0,002142	54	27	0,003285	54	29,4	0,000154
68	74,2	0,002079	68	28,4	0,003123	68	29,4	0,000154
80	76,6	0,002014	80	30,3	0,002928	80	29,4	0,000154
95	78	0,001978	95	30,8	0,002881	95	29,2	0,000155
115	81,5	0,001894	115	32,4	0,002739	115	29,2	0,000155
150	86,8	0,001779	150	35,3	0,002515	150	29,2	0,000155
190	90,7	0,001704	190	37,6	0,002362	190	28,5	0,000158

4. Графики зависимости α_ρ = f(T)

5. Зависимость удельного сопротивления и температурного коэффициента удельного сопротивления от состава сплава

Значения удельного сопротивления сплавов находим из формулы:

ρ_Cu-Ni = ρ_Nix_Ni + ρ_Cu(1-x_Ni) + Cx_Ni(1 – x_Ni)

Коэффициент С находим, подставляя вместо ρ_Cu-Ni значение удельного сопротивления константана, а x_Ni принимаем равным 0,4, так как содержание никеля в константане

равно 40%.

Коэффициент С равен 2,150*10^-6.

Значения температурного коэффициента удельного сопротивления находим по формуле:

αρ_Cu-Ni = (1/ ρ_Cu-Ni)[ αρ_Cu*ρ_Cu(1-x_Ni) + ρ_Nix_Niαρ_Ni ],

где значение ρ_Cu-Ni берется из предыдущей формулы.

Таблица зависимости ρ и αρ от состава сплава:

xNi	0	0,2	0,4	0,6	0,8	1
ρ, мкОм*м	0,014	0,368	0,551	0,561	0,400	0,066
αρ, К-1	0,00230	0,00021	0,00022	0,00030	0,00053	0,00390

Примечание Значения αρ для никеля и меди брались при температуре 27˚C.

6. Графики зависимостей ρ(x_ni-cu) и αρ(x_ni-cu)

7. Графики зависимости термоЭДС от температуры

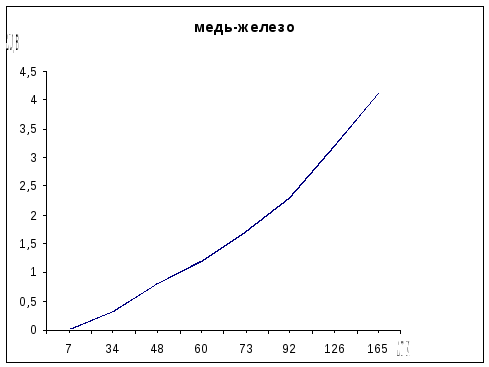
8. Выводы

1. Удельное сопротивление сплава больше любого из удельных сопротивлений металлов, входящих в этот сплав.

2. Сопротивление константана практически не меняется в широком диапазоне температур.

3. Зависимость ∆U(∆Т) для термопар можно аппроксимировать линейной зависимостью

y=k*x, где k – удельная термоэлектродвижущая сила, x = ∆Т.

4. Удельное сопротивление сплава имеет параболическую зависимость от содержания в сплаве одного из его компонентов.