3. Классификация на основе обычного евклидова расстояния
и принципа «центра тяжести».
Так как мы используем обычное евклидово расстояние, то матрица R1 останется без изменения. Согласно алгоритма объединим в один кластер цеха 4 и 5, как наиболее близкие 2,24.
Кластер S(4,5) охарактенизуем его центром тяжести, для этого используем вектор средних :
Расстояние от этого кластера до объектов равно:
Тогда матрица расстояний примет вид:
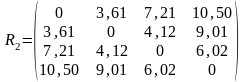
Объединим объекты 1 и 2, расстояние между которыми минимальное 3,61. Тогда кластер будет характеризоваться центром тяжести:
Определим новые расстояния:
Тогда матрица расстояний примет вид:
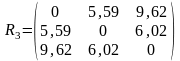
Объединим кластеры S(1,2) и S(3), так как расстояние между ними минимально 5,59. Определим его вектор средних
Найдем расстояние между кластерами S(1,2,3) и S(4,5)
Составим матрицу расстояний:
На основании графического представления результатов кластерного анализа по принципу «центра тяжести» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(,4,5) , когда пороговое расстояние находится в интервале 5,59 pпор 8,17.
Таким образом, используя принцип «центр тяжести» мы получили разбиение цехов, которое отличается от разбиения по принципу «дальнего соседа», но совпадает с расчетами в первом варианте по принципу «ближнего соседа».
Графические результаты классификации представлены на рис.
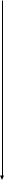
p 8,17
8
7
6 5,59
5
4 3,61
3
2 2,24
1
0
-
1
2
3
4
5
цеха
Рис. Дендрограмма (обычное евклидово расстояние, «центр тяжести»)
4. Классификация на основе обычного евклидова расстояния
и принципа «средней связи».
Так как мы используем обычное евклидово расстояние, то матрица R1 останется без изменения. Согласно алгоритма объединим в один кластер цеха 4 и 5, как наиболее близкие 2,24. Расстояние от этого кластера до объектов по принципу «средней связи» равно:
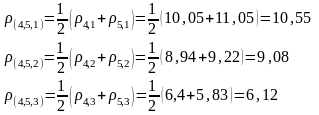
Тогда матрица расстояний примет вид:
Объединим объекты 1 и 2, расстояние между которыми минимальное 3,61. Определим новые расстояния:
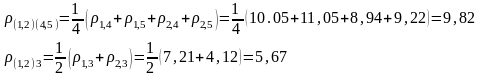
Тогда матрица расстояний примет вид:
Объединим кластеры S(1,2) и S(3), так как расстояние между ними минимально 5,67. Найдем расстояние между кластерами S(1,2,3) и S(4,5)
Графические
результаты классификации представлены
на рис.
p 8,58
8
7
6 5,67
5
4 3,61
3
2 2,24
1
0
-
1
2
3
4
5
цеха
Рис. Дендрограмма (обычное евклидово расстояние, «средняя связь»)
На основании графического представления результатов кластерного анализа по принципу «средней связи» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(,4,5) , когда пороговое расстояние находится в интервале 5,67 pпор 8,58.
Таким образом, используя принцип «средней связи» мы получили разбиение цехов, которое отличается от разбиения по принципу «дальнего соседа», но совпадает с расчетами в первом варианте по принципу «ближнего соседа» и «центра тяжести».
Следовательно при классификации 5 цехов предприятия предпочтительным является объединение в одну группу 4 и 5 цеха, а во вторую 1,2 и 3 цехов, что подтверждено тремя вариантами расчетов из четырех.