1. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип “ближайшего соседа”.
Построим матрицу расстояний
Матрица расстояний рассчитана на основе обычного евклидова расстояния между наблюдениями.
Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки 4,5=2,24 и поэтому объединим их в один кластер. После объединения объектов имеем четыре кластера: S1, S2, S3, S(4,5).
очевидно, что 1,1=0.
Примечание: На основании предварительного качественного анализа было выдвинуто предположение, что по поведению три первые цеха принадлежат одной типологической группе, а два последних (4 и 5) – другой, что согласуется с расположением пяти наблюдений на плоскости, представленных на рис. .
1
2
1
0
8
6
4
2
0
-
5
10
15
Рис. Исходные данные для классификации
Расстояние между кластерами будем находить по принципу “ближайшего соседа”, воспользовавшись формулой пересчета. Так расстояние между кластером S1 и кластером S(4,5) равно:
Мы видим, что расстояние 1,(4,5) равно расстоянию от объекта 1 до ближайшего к нему объекта, входящего в кластер S(4,5), т.е. 1,(4,5)= 1,4=10,05. Проводя анологичные расчеты, получим матрицу расстояний
Объединим наблюдения 1 и 2, имеющие наименьшее расстояние 1,2=3,61. После объединения имеем три кластера S(1,2), S3, и S(4,5)
Вновь строим матрицу расстояний. Для этого необходимо рассчитать расстояния до кластера S(1,2).
Получим новую матрицу расстояний
Объединим кластеры S(1,2) и S3, расстояние между которыми, согласно матрице R3, минимально 4,12. В результате этого получим два кластера: S(1,2,3) и S(4,5).
p
6 5,83
5 4,12
4 3,61
3 2,24
2
1
0
-
1
2
3
4
5
цеха
Рис. Дендрограмма (обычное евклидово расстояние, ближайший сосед)
Определим между ними расстояние:
На основании графического представления результатов и кластерного анализа можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(4,5) , когда пороговое расстояние находится в интервале 4,12 pпор 5,83.
2. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип «дальнего соседа».
Как и в предыдущем расчете, мы используем обычное евклидово расстояние, поэтому матрица R1 останется без изменения. Согласно алгоритму объединим цеха 4 и 5 в один кластер, как наиболее близкие по расстоянию 2,24. После объединения имеем четыре кластера S(1), S(2), S(3) и S(4,5).
В виду того, что расстояние между кластерами измеряем по принципу «дальнего соседа», то воспользуемся формулой пересчета:
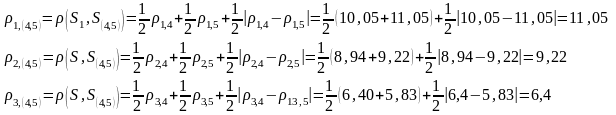
Таким образом, расстояние между кластерами 1 и (4,5) максимально и составляет 11,05. Построим новую матрицу расстояний:
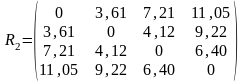
Объединим объекты 1 и 2 в один кластер, как наиболее близкие (расстояние между ними 3,61. После объединения имеем три кластера: S(1,2), S(3) и S(4,5). Определим новые расстояния между кластерами:
Строим
матрицу расстояний R3,
используя принцип «дальнего соседа».
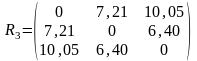
Объединим кластеры S(3) и S(4,5), так как расстояние между ними минимально 6,40. Определим расстояние между новыми кластерами S(1,2) и S(3,4,5):
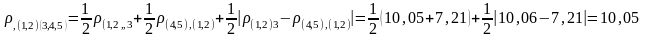
Составим матрицу расстояний:
На основании графического представления результатов кластерного анализа по принципу «дальнего соседа» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2) и S(3,4,5) , когда пороговое расстояние находится в интервале 6,40 pпор 10,05.
Таким образом, используя принцип «дальнего соседа» мы получили разбиение цехов, которое отличается от разбиения по принципу «ближнего соседа».
p
12
10 10,05
8
6 6,40
4 3,61
2 2,24
0
-
1
2
3
4
5
цеха
Рис. Дендрограмма (обычное евклидово расстояние, «дальний сосед»)