2.2. Пример решения работы

Задание №6. Решить матричное уравнение, сделать проверку.

.

Решение

Запишем данное уравнение в матричной форме:

, где

; ; .

Преобразуем уравнение к виду и выполним действия с матрицами в правой части:

.

Обозначим полученную матрицу и запишем уравнение в виде . Умножив обе части последнего равенства на справа, получим:

.

Имея в виду, что , решением данного уравнения будет , где − матрица, обратная матрице .

Найдём обратную матрицу так, как описано в разделе 2.1.1. на стр. 15, тогда

.

Найдем решение данного уравнения, умножив матрицу на матрицу . Напомним, что одну матрицу на другую можно умножать тогда и только тогда, когда число столбцов первой матрицы равно числу строк второй. В нашем случае матрица имеет размер , а матрица − , значит, произведение имеет смысл (3=3), причем, при умножении получится матрица размера .

По правилу умножения получим:

.

Итак, .

Проверим найденное решение, подставив его в исходное уравнение:

.

Так как найденное решение обращает уравнение в тождество, то решение найдено верно.

Ответ: .

Задание №7. Дана функция , график которой проходит через три заданные точки , , . Найти параметры , , , решив получившуюся систему методом Гаусса, построить график функции .

Решение

Подставим координаты заданных точек в уравнение :

Получим систему трех линейных уравнений с тремя неизвестными для нахождения коэффициентов , , :

.

Решим систему методом Гаусса. Запишем расширенную матрицу системы:

.

Выполним над этой матрицей необходимые элементарные преобразования. Обнулим все элементы первого столбца, кроме первого элемента. Для этого умножим последовательно первую строку на , и на и прибавим ее ко второй и третьей строке соответственно:

Разделим все элементы второй строки на , а третьей − на :

Обнулим третий элемент второго столбца. Для этого вторую строчку умножим на и прибавим к третьей:

Разделим третью строчку на 2:

.

Матрица приведена к ступенчатому виду. Этой матрице, которая эквивалентна матрице , соответствует следующая система, равносильная данной:

Прямой ход метода Гаусса закончен. В результате обратного хода получим:

Таким образом, получаем решение системы: .

Сделаем проверку:

Так как все уравнения системы обратились в тождества, то решение верное.

Но тогда

.

− уравнение параболы с вершиной в точке , которая проходит через три данные точки , , , пересекает ось в точке , ось не пересекает, так как уравнение не имеет действительных корней.

Построим график функции .

Задание №8. Решить систему уравнений по формулам Крамера:

.

Решение

Вычислим главный определитель системы:

.

Так как , то данная система имеет единственное решение, которое найдем по формулам Крамера:

; ; .

Вычислим вспомогательные определители:

.

.

.

Но тогда

; ; .

Ответ: ; ; .

Задание №9. Решить уравнение . Ответ представить в тригонометрической форме. Модуль вычислить с точностью до 0,01, а аргумент в градусах. Изобразить полученные числа на комплексной плоскости.

Решение

Очевидно, что из .

Чтобы выполнить деление комплексных чисел, умножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на , получим:

.

Итак, . Очевидно, чтобы решить это уравнение надо найти все значения . Обозначим .

Известно, что корень n−й степени из комплексного числа имеет n различных значений, которые находятся по формуле:

,

где ; .

Найдём тригонометрическую форму комплексного числа как описано в разделе 2.1.3.: ;

Тогда число в тригонометрической форме для нашего примера будет иметь вид:

.

Но тогда .

Полагая , найдем

или

или

или .

И зобразим полученные числа , на комплексной плоскости.

Раздел 3. Контрольная работа по математике №3

Введение в математический анализ

3.1. Теоретический материал

3.1.1. Основы теории пределов функций

Понятие предела функции

Независимая переменная величина , входящая в понятие функции, может, в соответствии с условиями конкретной задачи, изменяться различным образом. Например, пусть принимает такую последовательность значений:

Видно, что с увеличением номера значение приближается к 3, что кратко обозначают ( стремится к 3). Если приближается к некоторому числу со стороны меньших значений (как в приведенном примере), то говорят, что стремится к слева и обозначают: ; если же приближается к со стороны больших значений, то говорят, что стремится к справа и обозначают: . Например, запись означает, что может, в частности, принимать такую последовательность значений: 3,1; 3,01; 3,001; ...

Если в своем изменении независимая переменная может стать больше любого наперед заданного положительного числа, то это обозначают так: ( стремится к бесконечности). Если при изменении независимой переменной она может стать меньше любого наперед заданного отрицательного числа (как угодно большого по модулю), то это обозначают так: ( стремится к минус бесконечности).

Ясно, что при изменении аргумента связанная с ним функция будет также принимать соответствующий ряд значений. Рассмотрим, например, функцию . Одновременное изменение и аргумента и функции удобно представить таблицей:

x	1	10	100	1000
f(x)	3	1,2	1,02	1,002

Из таблицы видно, что при неограниченном увеличении значения функции приближаются к 1.

Число называется пределом (или предельным значением) функции при , если для любой последовательности значений аргумента , стремящейся к , соответствующая последовательность значений функции стремится к .

Для обозначения предела используют следующую символику:

(lim – начало латинского слова limit – предел).

Функция называется бесконечно малой при , если ее предел при равен 0.

Например, рассмотрим функцию . Составим таблицу

	1	10	100
	1	0,01	0,0001

Можно заключить, что .

В общем случае .

Функция называется бесконечно большой при , если с приближением к , модуль значения функции становится больше любого наперед заданного положительного числа.

Символически такое поведение функции описывают так:

.

В формулировке понятия предела предполагалось, что может быть и конечным числом и . Если рассматривать только конечные значения , то можно ввести понятие одностороннего предела.

Число называется правым пределом функции в точке , если для любой последовательности значений аргумента, сходящейся к и состоящей из чисел, больших , соответствующая последовательность значений функции сходится к .

Число называется левым пределом функции в точке , если для любой последовательности значений аргумента, сходящейся к и состоящей из чисел, меньших , соответствующая последовательность значений функции сходится к .

Рассмотрим функцию , найдем ее односторонние пределы в точке . Для предела слева составим таблицу:

x	0	0,5	0,9

Значения функции, представленные в таблице, позволяют заключить, что .

Для предела справа составим такую таблицу:

x	2	1.5	1.1
	2

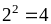
Из данных этой таблицы можно сделать вывод: .