Контрольная работа №2 Элементы линейной алгебры
51-60. Решить матричное уравнение. Сделать проверку.
51.
.
52.
.
53.
.
54.
55.
56.
57.
58.
59.
60.
61-70. Дана функция , график которой проходит через три заданные точки , , . Найти параметры , , , решив получившуюся систему методом Гаусса, построить график функции .
61. |
|
|
|
62. |
, |
|
|
63. |
, |
|
|
64. |
, |
|
|
65. |
|
|
|
66. |
|
|
|
67. |
, |
|
|
68. |
, |
|
|
69. |
|
|
|
70. |
|
, |
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
71-80.Решить систему уравнений по формулам Крамера.
71.
|
76.
|
72.
|
77.
|
73.
|
78.
|
74.
|
79.
|
75.
|
80.
|
.
.
.
.
.
.
.
.
.81-90. Решить данное уравнение. Ответ представить в тригонометрической форме. Модуль вычислить с точностью до 0,01, а аргумент в градусах. Изобразить полученные числа на комплексной плоскости.
81.
|
86.
|
82.
|
87.
|
83.
|
88.
|
84.
|
89.
|
85.
|
90.
|
.
.
.
.
.
.
.
.
.
.Контрольная работа №3 Введение в математический анализ
91-100. Найти пределы, не пользуясь правилом Лопиталя.
91. а)
|
||
б)
|
в)
|
г)
|
92. а)
|
||
б)
|
в)
|
г)
|
93. а)
|
||
б)
|
в)
|
г)
|
94. а)
|
||
б)
|
в)
|
г)
|
95. а)
|
||
б)
|
в)
|
г)
|
96. а)
|
||
б) ; |
в)
|
г)
|
97. а)
|
||
б)
|
в)
|
г)
|
98. а)
|
||
б)
|
в)
|
г)
|
99. а)
|
||
б)
|
в)
|
г)
|
100. а)
|
||
б)
|
в)
|
г)
|
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.101-110. Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертеж.
101.
|
106.
|
102.
|
107.
|
103.
|
108.
|
104.
|
109.
|
105.
|
110.
|
111-120. а) Дана функция
.
Найти значение функции и значение
производной
в указанной точке.
б) Найти производные данных функций.
111. а)
|
б.1)
|
б.2)
|
б.3)
|
112. а)
|
б.1)
|
б.2)
|
б.3)
|
113. а)
|
б.1)
|
б.2)
|
б.3)
|
114. а)
|
б.1)
|
б.2)
|
б.3)
|
115. а)
|
б.1)
|
б.2)
|
б.3)
|
116. а)
|
б.1)
|
б.2)
|
б.3)
|
117. а)
|
б.1)
|
б.2)
|
б.3)
|
118. а)
|
б.1)
|
б.2)
|
б.3)
|
119. а)
|
б.1)
|
б.2)
|
б.3)
|
120. а)
|
б.1)
|
б.2)
|
б.3)
|
;
,
,
.
;
,
,
.
;
,
,
.
;
,
,
.
;
,
,
.
;
,
,
.
;
,
,
.
;
,
,
;
,
,
.
;
,
,
.121-130. Показать, что функция удовлетворяет данному уравнению.
121.
|
|
122.
|
|
123.
|
|
124.
|
|
125.
|
|
126.
|
|
127.
|
|
128.
|
|
129.
|
|
130.
|
|
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
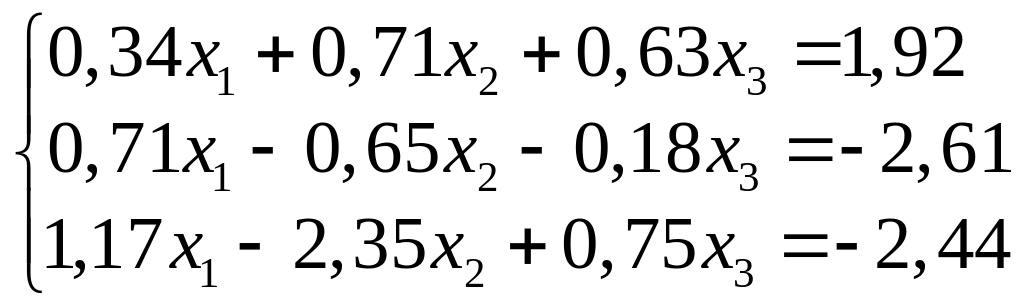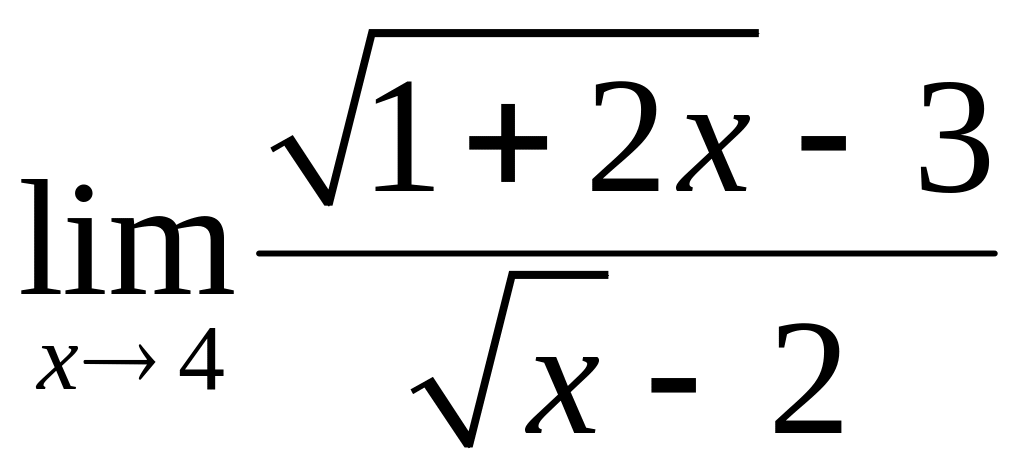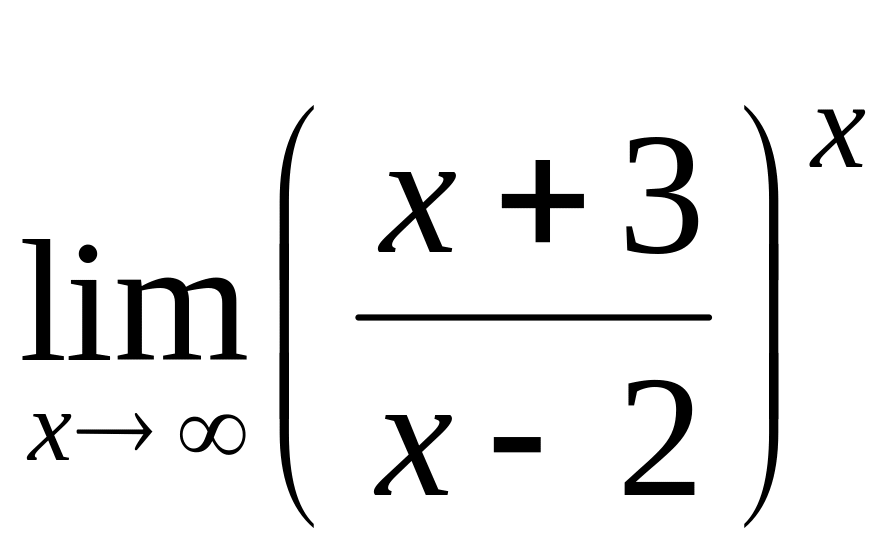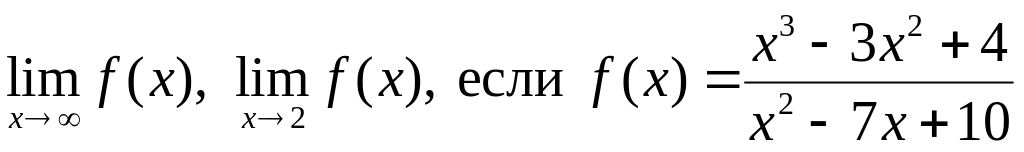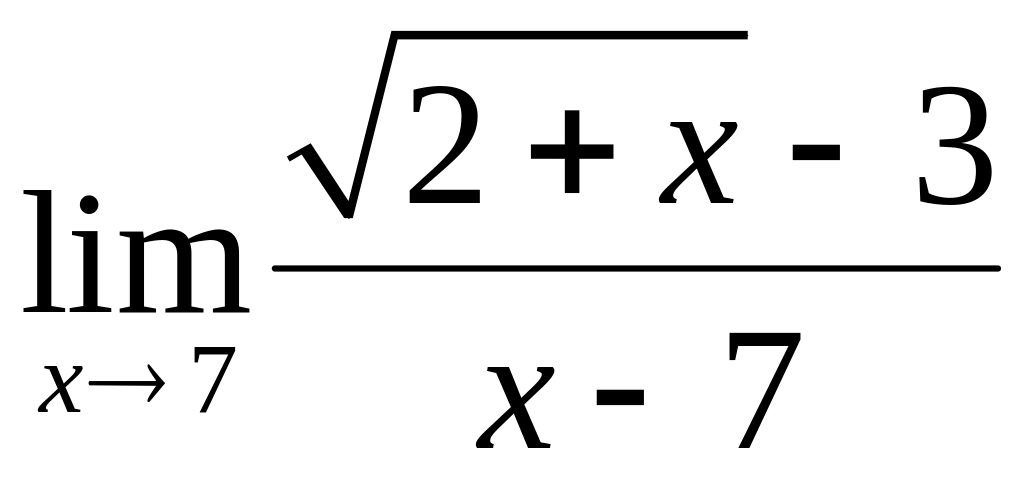