1.1 Апериодическое звено

Принципиальная схема апериодического звена приведена на рис. 1.1.1[2]

Рис. 1.1.1. Принципиальная схема (а) и схема распределения токов и падений напряжений на элементах апериодического звена (б)

Передаточная функция звена представляется следующим выра­жением[2]:

W(p)= = = , (1.1.1)

К= - коэффициент ослабления информационного сигнала;

T= - постоянная времена звена;

T₁= - постоянная времени.

Определяем изображение по Лапласу переходной характеристики (З):

h(p)= . (1.1.2)

Преобразуем изображение переходной характеристики (1.1.2) в оригинал с разложением знаменателя изображения (1.1.2) на про­стые множители и используя приложение I [l]:

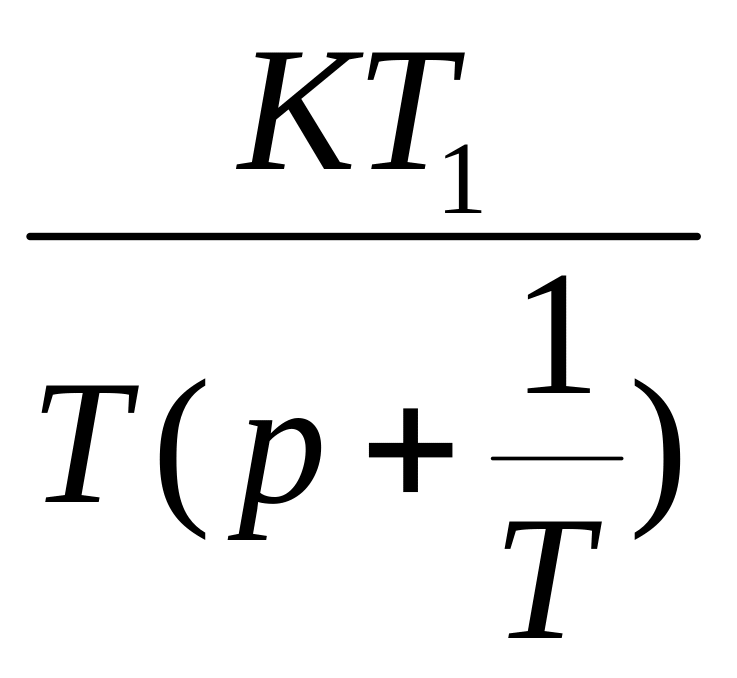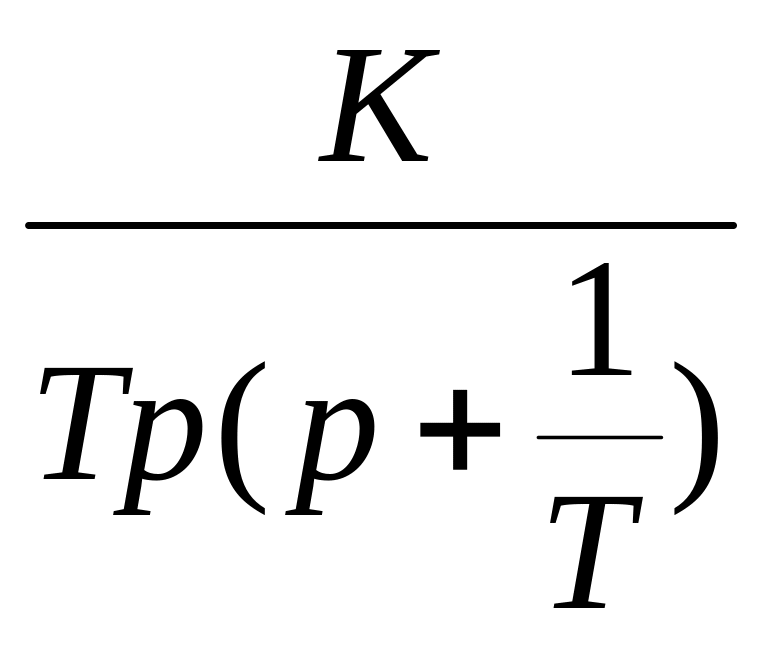
h(p)= + h(t)=K(1-(1- )e ) . (1.1.3)

Определяем импульсную (весовую) характеристику по (6) и (1.1.3)

K(t)= = (1- )e . (1.1.4)

Графики переходной и импульсной функций, построенных по их аналитическим выражениям (1.1.3) и (1.1.4), приведены на рис.1.1.2

Рис. 1.1.2. Временные характеристики апериодического звена: а - переходная функция; б - импульсная (весовая) функция

1.2 Дифференцирующее звено

Принципиальная схема дифференцирующего звена приведена на рис. 1.2.1.[2]

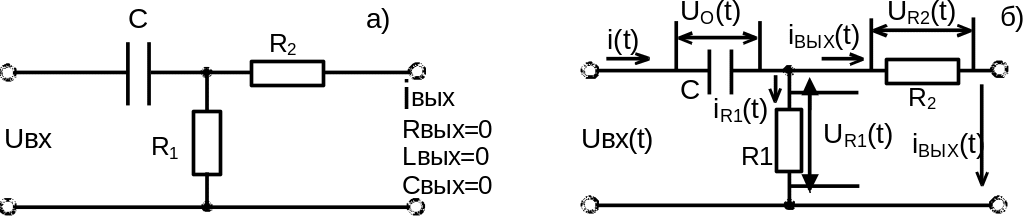
Рис. 1.2.1. Принципиальная схема (а) и схема распределения токов и падений напряжений на элементах дифференцирующего звена (б)

Передаточная функция дифференцирующего звена представля­ется следующим выражением[2]:

W(p)= = = , (1.2.1)

где К = коэффициент ослабления сигнала;

- постоянная времени звена.

Определяем изображение по Лапласу переходной характерис­тики по (З):

h(p)= . (1.2.2)

Преобразуем изображение переходной характеристики (1.2.2) в оригинал, используя приложение А:

h(p)= . (1.2.3)

Определяем импульсную (весовую) характеристику по (6) и (1.2.3)

k(t)= . (1.2.4)

7

Графики переходной и импульсной функций, построенных по их аналитическим выражениям (1.2.3) и (1. 2.4), приведены на рис. 1.2.2.

Рис. 1.2.2. Временные характеристики дифференцирующего звена:

а - переходная функция; б - импульсная (весовая) функция

1.3. Интегрирующее звено

Принципиальная схема интегрирующего звена приведена на рис. 1.3.1 [2].

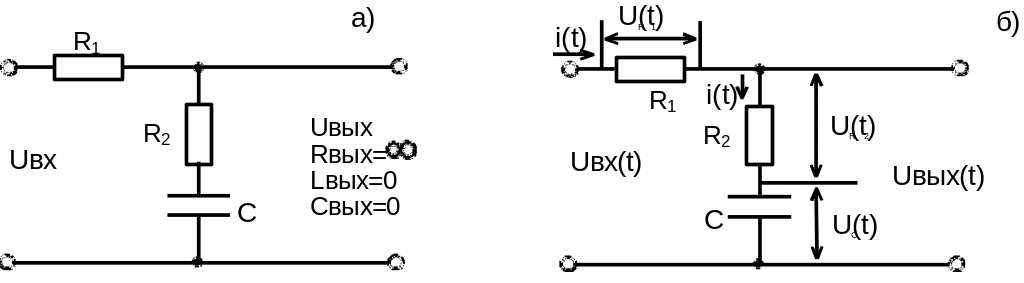
Рис. 1.3.1. Принципиальная схема (а) и схема распределения

токов и падений напряжений на элементах интегрирующего звена (б)

Передаточная функция интегрирующего звена представлена следующим выражением [2]:

W(p)= = = , (1.3.1)

где T₁=(R₁+R₂)С - постоянная времени интегрирования;

T₂₌R₂С - постоянная времени форсирования.

При R₁>> и R₂ R₁ имеем

W(p) . (1.3.2)

Определяем переходную характеристику в изображении по Лапласу, используя выражение (3):

h(p)= . (1.3.4)

Преобразуем изображение (1.3.4) в оригинал по приложению1 [1]:

h(p)= 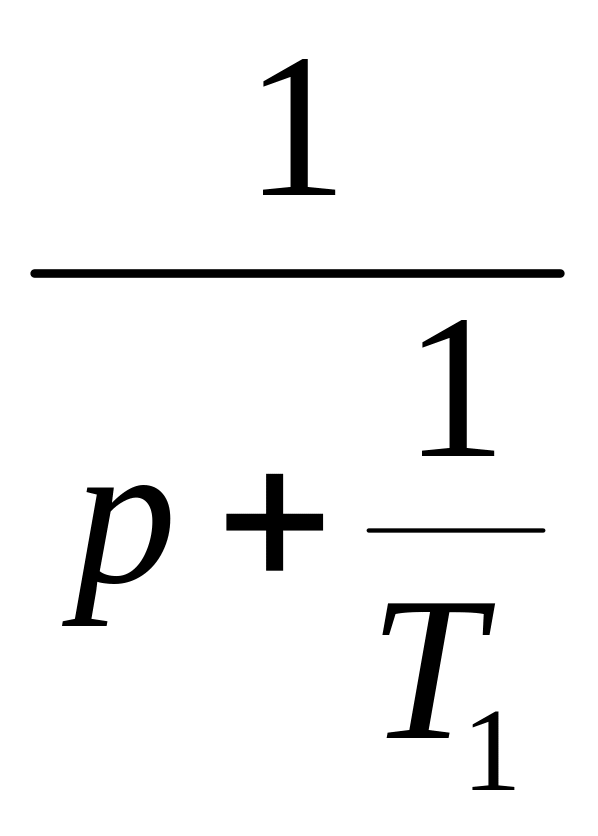+ h(t) = + =(1-(1- ) ). (1.3.5)

Определяем импульсную (весовую) характеристику по (6) и (1.3.5):

k(t)= = ( - ) . (1.3.6)

Графики переходной и импульсной функций, построенных по их аналитическим выражениям (1.3.5) и (1.3.6), приведены на рис. 1.3.2..

Рис. 1.3.2. Временные характеристики интегрирующего звена:

а - переходная функция; б - импульсная (весовая) функция

9