10

Лекция 8. Качество работы сау

8.1. Показатели качества сау

Качество системы имеет смысл выяснять только после установления, что она устойчива. Наглядно представление о динамических свойствах САУ, ее качестве дает переходная функция. Качество системы характеризуется следующим: как быстро система реагирует на возмущения и как сильно их подавляет, каким путем она приходит в установившееся состояние и насколько точно воспроизводятся системой полезные сигналы после того, как установившееся состояние достигнуто.

Комплекс требований, определяющих поведение системы в установившемся и переходных процессах отработки заданного воздействия объединяется понятием качества процесса управления (качества системы).

К основным показателям качества САУ относятся:

- быстродействие, t_пп;

- перерегулирование ;

- колебательность М;

- статическая и динамическая точность;

- добротность системы.

Быстродействие характеризуется (рис.1.7.1):

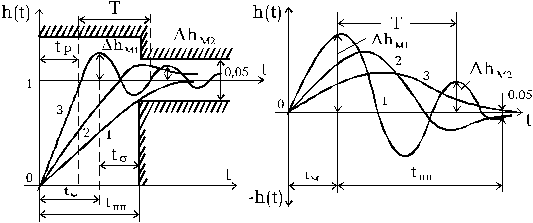
Рис.1.7.1. Типовые переходные функции САУ и показатели качества: а - управляющее воздействие; б - возмущающее воздействие; I - монотонные; 2 - апериодические; 3 - колебательные

а) общим временем переходного процесса t_пп, за которое выходная величина h(t) войдет в 5% зону. Современные САУ требуют t_пп0,04-0,1;

б) временем первого согласования (регулирования) t_p за которое h(t) первый раз достигнет предполагаемого установившегося состояния;

в) временем первого максимума t_м;

г) временем затухания первого перерегулирования t_М.

Перерегулирование % определяется максимальным отклонением выходной величины (перерегулирование h₁), отнесенным к ее заданному установившемуся значению.

Считается нормальным , допускается до 50%, но в ряде случаев требуется 5%.

Колебательность характеризуется 4-мя показателями:

1. Показатель колебательности М, представляющий собой резонансное значение амплитудно-частотной характеристики замкнутой системы в относительных единицах

M=f() или .

В хорошо сдемпфированных системах с перерегулированием не более 20-30% показатель М=1,1...1,3. Допускается до 1,6...1,8 при норме 1,3...1,5.

2. Числом колебаний n в одну сторону за время t_пп. Чаще всего допускают n=1...2, а иногда 3...4.

3. Декрементом затухания , равным отношению модулей двух сменных перегулирований

=h_м1/h_м2.

4. Угловой частотой колебаний _к=2/T_к .

Добротность системы , где W_(P)=D₀+D_скP+D_ускP²; W_(P)= определяется по ЛАЧХ, продлив низкочастотную асимптоту, идущую с наклоном 20 дБ/дек, до пересечения с осью частот. Получим добротность системы по скорости. До пересечения с осью частот продлим низкочастотную асимптоту, идущую с наклоном 40 дБ/дек, и получим добротность по ускорению.

По среднечастотному участку ЛАЧХ определяют приблизительные показатели качества САУ.

8.2. Точность сау и астатизм

Точность воспроизведения управляющих воздействий - одно из важнейших требований, предъявляемых к системам автоматического управления. Так как в реальных условиях действующие на систему управляющие (входные) и возмущающие воздействия носят случайный характер, приходится рассматривать ее свойства при действии различных типовых воздействий.

Оценку САУ проводят обычно для четырех наиболее часто применяемых режимов: неподвижное состояние, движение с постоянной скоростью, движение с постоянным ускорением, движение по гармоническому (синусоидальному) закону.

При постоянных управляющих X(t)=X₀=Const и возмущающих F(t)=F₀=Const воздействиях устанавливают статическую ошибку, которую определяют соответствующими передаточными функциями системы

₀=_x0+_F0= . (1.7.1)

С учетом W(0)=K и W_F(0)=K_F - коэффициентов передачи разомкнутой системы получим

. (1.7.2)

Статическая ошибка в астатических системах теоретически отсутствует, а практически имеется из-за недостаточной чувствительности. Также отсутствует теоретическая ошибка по скорости из-за _ск=0.

В статических системах ошибка складывается из статической ошибки ₀ и скоростной _ск:

_уст.ск.=₀+_ск.=₀+v₀/K_ск. (1.7.3)

Астатизм (ошибка по ускорению) систем 2-го порядка оценивается

_уск=v/K_уск.

Ошибки системы по ускорению, если задано его значение, легко определить по логарифмической амплитудно-частотной характеристике, продолжив ее вторую асимптоту до пересечения с осью частот, найдя ₀, а затем и K_уск = .

Пример. Для заданных воздействий: скоростное v=20мм/с, постоянное ускорение =3мм/c²,гармоническое с амплитудой X_max=4мм и период T_n=8c, определим ошибки астатической системы автоматической ориентации сварочного электрода.

,

где K=6,6, T₁=0,12 с; T₂=0,05 с.

Чувствительность двигателя U_тр=6B (напряжение трогания). Находим статическую ошибку, исходя из параметров системы:

₀=U_тр/K=6/6,6=0,9мм.

Скоростная ошибка

_ск=v/K₀=20/6,6=3мм.

Для определения ошибки при воспроизведении гармонического воздействия сначала находим его частоту _n=2/T_п=0,8c^-1, затем модуль частотной функции L'() на этой частоте по ЛАЧХ (рис.1.5.5) A(_n)=6,3.

_{max уст}=X_max(_n)=4/6,3=0,6мм.

Таким образом, исследованная на точность система, содержащая только функционально необходимые элементы, характеризуется очень малой точностью при всех видах воздействий и нуждается в совершенствовании с помощью коррекции.