Контрольные карты (карты шухарта) по количественным признакам в программе excel

Цель работы: ознакомиться с методикой построения контрольных карт по количественным признакам с помощью программы Excel.

Задание: 1. Построить контрольные карты по количественным признакам в программе Excel.

2. Определить причины появления дефектов и разработать рекомендации по устранению брака.

Основные сведения

Контрольные карты представляют собой разновидности графиков, но отличаются тем, что имеют контрольные границы (границы регулирования). Если все значения (точки) окажутся внутри контрольных границ (рис. 4.1 а), то процесс рассматривается как управляемый (стабильный).

Рис. 4.1. Контрольные карты и контрольные границы

Если на графике есть точки, выходящие за пределы контрольных границ (рис. 4.1 б), то это свидетельствует о наличии погрешности и неуправляемости процесса. Различают контрольные карты двух типов: - для непрерывных и дискретных значений или по качественным и количественным признакам.

Контрольные карты по количественным признакам в Excel

Контрольные карты по количественным признакам (табл. 4.1) используются для статистического контроля и регулирования технологического процесса. Регулирование по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у выборки продукции. Затем по фактическим значениям контролируемого показателя определяются статистические характеристики процесса и по ним принимаются решения о его состоянии.

Таблица 4.1. Виды контрольных карт

Значение характеристики	Название карты	Применение
Непрерывные. Регулирование по количественному признаку.	- карта ( -среднее значение и R - выборочный размах)	Для анализа и управления процессами показатели, качества которых представляют собой непрерывные величины.
	x - карта медиан (измеряемое значение)	Если группирование данных не эффективно или данные о процессе поступают через большие интервалы. В этом случае данные отдельными точками наносятся на график по мере их поступления.
	s-карта – средних квадратичных отклонений
Дискретные. Регулирование по качественному признаку.	рn-карта числа дефектных единиц продукции	Для контроля числа дефектов при постоянном объеме выборки п.
	р - карта доли дефектной продук-ции контрольной выборки	При контроле и регулировании технологического процесса.
	с - карта числа дефектов	Для числа дефектов в изделиях одинакового размера
	и - карта числа дефектов на единицу продукции	Для числа дефектов изделий разного размера

Такими характеристиками являются выборочное среднее и медиана (характеристики положения), а также размах и выборочное среднее квадратическое отклонение (характеристики рассеяния случайной величины Х).

На контрольную карту наносят значения некоторой статистической характеристики (точки), которые рассчитываются по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы Кв (или UCL) и Кн (или LCL), верхнюю и нижнюю границы технических допусков Тв и Тн (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы Кп.

Для расчета границ и построения контрольной карты используют обычно 20 … 30 точек.

По расположению точек относительно границ судят о настроенности или разладки технологического процесса. Обычно процесс считается разлаженным в следующих случаях:

1. Некоторые точки выходят за контрольные пределы.

2. Серия из семи точек оказывается по одну сторону от средней линии.

Кроме того, если по одну сторону от средней линии находятся:

А) десять из серии в одиннадцать точек;

Б) двенадцать из серии в четырнадцать точек;

В) шестнадцать из серии в двадцать точек.

3. Есть дрейф, т.е. точки образуют возрастающую или нисходящую непрерывно кривую.

4. Две — три точки оказываются за предупредительными двухсигмовыми границами.

5. Приближение к центральной линии. Если большинство точек находится внутри полуторасигмовых линий, это значит, что в подгруппах смешиваются данные из различных распределений.

6. Имеет место периодичность, т.е. то подъем, то спад с примерно одинаковыми интервалами времени.

7. Контрольные границы шире поля допуска. В идеальном случае достаточно, чтобы контрольные границы составляли 3/4 величины поля допуска.

Если процесс отлажен (достигнута необходимая точность и стабильность), на контрольную карту продолжают наносить точки, но через 20…30 точек пересчитывают контрольные границы. Они должны совпадать с исходными границами.

Если контрольная карта показывает, что процесс разлажен, находят причины разладки и устраняют их.

По количественным признакам используют в основном следующие контрольные карты:

- карта средних арифметических значений ( — карта);

- карта медиан ( — карта);

- карта средних квадратичных отклонений (s-карта);

- карта размахов (R-карта).

Для – карты и - карты – рассчитывают две границы регулирования или контроля: верхнюю и нижнюю.

Для s– карты и R- карты – достаточно рассчитать по одной границе контроля - верхней, так как можно следить лишь за увеличением рассеивания.

Карта средних арифметических значений ( —карта) используется для контроля отклонения параметра от нормы и настройки в норму. Точки на контрольной карте — это средние значения небольших выборок, обычно одинакового объема, с 3 до 10 элементов:

,

где n — объем выборки (подгруппы).

Для получения выборок можно использовать результаты измерений, проводившихся через равные промежутки времени, путем разбиения их на группы.

Среднюю линию рассчитывают как среднее из средних значений выборок:

,

где k — число подгрупп (число точек). Обычно k = 20 … 30.

Контрольные границы рассчитывают по формуле:

, где

σ- среднее квадратическое отклонение всей совокупности данных.

В этом выражении (как и при расчете контрольных границ для других видов контрольных карт) коэффициент 3 используется, исходя из правила трех сигм.

Карта медиан ( -карта) используется вместо карты средних значений, когда хотят упростить расчеты. Точки на карте - это медианы выборок одинакового объема с 3 до 10 элементов. Медиана - это при нечетном объеме выборки середина вариативного ряда, при четном объеме выборки - среднее из двух значений середины вариативного ряда.

Средняя линия - это среднее из медиан выборок. Контрольные границы определяют по формуле:

Карта медиан менее точная, чем карта средних значений.

При использовании для расчетов компьютера применения карты медиан вместо карты средних значений вряд ли оправдано.

Карта среднего квадратического отклонения (СКО) (s-карта) используется для контроля рассеяния показателя. Точки на карте - средние квадратические отклонения выборок одинакового объема с 3 до 10 элементов. Средняя линия - это среднее по СКО выборок. Контрольные границы:

, ,

где χ² - критерий Пирсона, n - объем выборки, α - уровень значимости. Обычно принимают α = 0,0027, что соответствует доверительной вероятности 0,9973. Часто на s-карте используют только верхнюю границу.

Карта размахов (R-карта) используется вместо карты средних квадратических отклонений, когда хотят упростить расчеты. При этом карта размахов менее точна.

При построении R-карты берут 20…30 выборок одинакового объема от 2 до 10 элементов. Точки на карте - размахи выборок.

Размах выборки R — это разность между максимальным x_max и минимальным x_min значениями выборки. Средняя линия 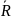- это среднее размахов выборок. Контрольные границы рассчитывают по формулам:

,

При уровне значимости 0,0027 коэффициенты D₃ и D₄ можно найти из табл. 4.2. При n <7 нижняя контрольная граница не используется.

Таблица 4.2. Значение коэффициентов для R-карты

N	2	3	4	5	6	7	8	9	10
D3	-	-	-	-	-	0,076	0,136	0,184	0,223
D4	3,267	2,575	2,282	2,115	2,004	1,924	1,864	1,816	1,777

Часто при статистическом регулировании технологических процессов используют двойные карты, указывающие как отклонение параметра от нормы, так и его рассеивание. Это могут быть, например, -карты или другие.

Таким образом, для определения границ регулирования необходимо знать параметры нормального распределения (математического ожидания) μ и среднего квадратического отклонения σ.

Пример 4.1. В швейном цехе принято решение перевести на статистическое регулирование технологический процесс дублирования деталей. Показателем качества избрана прочность клеевого соединения, равная 8,5 Н/см, и допускаются её отклонения: верхнее отклонение ES= -1,5 Н/см и нижнее - EI=-2,0 Н/см. Построить контрольную -карту и провести статистический анализ процесса.

Реализация статистического метода регулирования процесса дублирования осуществляется в три этапа:

1. Проводится предварительное исследование состояния процесса и определяется вероятная доля дефектной продукции и коэффициент воспроизводимости.

2. Строится контрольная карта и выбирается план контроля.

3. Проводится статистическое регулирование процесса дублирования.

На первом этапе для проведения исследований необходима информация о процессе. Для испытания отбираем выборку из 100 проб, контроль прочности клеевого соединения проводят через каждый час, при этом испытывают по пять проб, т.е. проводим 20 серий измерений. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества (8,5Н/см) приведены в табл. 4.3.

Таблица 4.3. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества

Цех швейный	Оборудование — пресс №1	Контролируемая операция — дублирование	Контроли-руемый параметр - ES= -1,5; 8,5; EI=-2,0
Объем контроля N = 100	Объем выборки n = 5	Средство контроля — прочность при расслаивании
Время	№ выборки	Результаты контроля - отклонение от показателя качества (8,5)
1	2	3	4	5	6	7
7.00	1	0,2	0,5	1	0,5	1
8.00	2	1,5	1	1	1,5	1,5
9.00	3	1,5	1,5	1	2	0,5
10.00	4	1,5	0,9	1,5	1,5	0,5
11.00	5	1,5	0,8	1,1	1	0,2
12.00	6	1	0,5	0,6	0,1	0,3
13.00	7	0,2	0,5	1	0,5	1
14.00	8	1,5	1	1	1,5	1,5
15.00	9	1,5	1,5	1	2	0,5
16.00	10	1,5	0,9	1,5	1,5	0,5
7.00	11	1,5	0,8	1,1	1	0,2
8.00	12	1	0,5	1,5	0,1	0,3
9.00	13	2	0,5	1	0,5	1
10.00	14	1,5	1	1	1,5	1,5
11.00	15	1,5	1,5	1	2	0,5
12.00	16	1,5	0,7	1,5	1,5	0,5
13.00	17	1,5	0,8	1,1	1	0,2
14.00	18	1	0,5	0,6	0,1	0,3
15.00	19	2	0,5	1	0,5	1
16.00	20	1,5	1	1	1,5	1,5

Определим среднее арифметическое каждой серии измерений:

,

где п =5, объем подгруппы (серии).

Вычисляем среднее значение всех опытов или среднее значение средних арифметических в каждой серии опытов. Оно является математическим ожиданием отклонения μ . и является средней линией диаграммы. Вычисляем контрольные линии. Строим график с нанесением всех точек.

Алгоритм построения контрольных карт по количественным признакам в Excel.

Новый лист Excel. В ячейку А1 вводим номер выборки, в ячейку В1 – контролируемый показатель (отклонение прочности при расслаивании от выбранного 8,5 Н/см). В диапазон А4:А23 вводим номера выборки (1-20).

В ячейки В4:F23 вводим данные результатов контрольных измерений - отклонения.

Сначала рассчитываем данные для построения контрольной карты средних арифметических значений ( —карта).

В ячейке G4 рассчитываем среднее значение первой выборки с помощью статистической функции СРЗНАЧ. Полученную формулу копируем в диапазон G5:G23.

В ячейке Н4 рассчитываем значение (Среднюю линию) как среднее из средних значений выборок с помощью статистической функции СРЗНАЧ.

В полученной формуле для диапазона ячеек вводим абсолютную адресацию и копируем формулу в диапазон Н5:Н23. Это необходимо для того, чтобы в дальнейшем можно было провести среднюю линию на контрольной карте.

В ячейке G27 рассчитываем среднее квадратическое отклонение (σ) всей совокупности результатов измерений s с помощью статистической функции СТАНДОТКЛОН для диапазона В4: F23.

В ячейке I4 рассчитываем нижнюю контрольную границу Кн. Формула в ячейке будет выглядеть так:=H4-3*G$27/КОРЕНЬ(5).

Указав абсолютную адресацию для имен ячеек, копируем значение из ячейки I4 в диапазон I5: I23. Это необходимо, чтобы в дальнейшем провести границу на карте.

В ячейке J4 рассчитываем верхнюю контрольную границу Кв. Формула в ячейке будет выглядеть так: =H4+3*G$27/КОРЕНЬ(5).

После указания абсолютной адресации для имен ячеек копируем формулу из ячейки J4 в диапазон J5: J23.

В ячейках К4 и L4 рассчитываем значение верхнего и нижнего технических допусков с учетом принятых допусков отклонения (+1,5 Æ 8,5-2,0).

В ячейках К5 вводим формулу: =8,5+1,5, затем копируем ее К5:К23 и получим верхнюю техническую границу Тв.

В ячейках L4 вводим формулу: =8,5-2 , затем копируем ее L5: L23 и получим нижнюю техническую границу Тн.

Таблица -карты имеет вид, табл. 4.4.

Таблица 4.4. Таблица данных для построения -карты

Номер подгруппы выборки			Кн	Кв	Тв	Тн
1	0,64	1,02	0,350476	1,689524	10	6,5
2	1,30	1,02	0,350476	1,689524	10	6,5
3	1,30	1,02	0,350476	1,689524	10	6,5
4	1,18	1,02	0,350476	1,689524	10	6,5
5	0,92	1,02	0,350476	1,689524	10	6,5
6	0,50	1,02	0,350476	1,689524	10	6,5
7	0,64	1,02	0,350476	1,689524	10	6,5
8	1,30	1,02	0,350476	1,689524	10	6,5
9	1,30	1,02	0,350476	1,689524	10	6,5
10	1,18	1,02	0,350476	1,689524	10	6,5
11	0,92	1,02	0,350476	1,689524	10	6,5
12	0,68	1,02	0,350476	1,689524	10	6,5
13	1,00	1,02	0,350476	1,689524	10	6,5
14	1,30	1,02	0,350476	1,689524	10	6,5
15	1,30	1,02	0,350476	1,689524	10	6,5
16	1,14	1,02	0,350476	1,689524	10	6,5
17	0,92	1,02	0,350476	1,689524	10	6,5
18	0,50	1,02	0,350476	1,689524	10	6,5
19	1,00	1,02	0,350476	1,689524	10	6,5
20	1,30	1,02	0,350476	1,689524	10	6,5

Cтроим -карту в программе Еxsel.

Во вкладке Вставка/ Диаграммы/ Точечная диаграмма с маркерами, на которой значение соединены отрезками. Для этого перед столбцом данных «средние арифметические подгрупп» вставьте столбец и скопируйте в него номера подгрупп от 1 до 20.

Выделить ячейки G4:K23, т.е все данные: номер подгруппы выборки, , верхнюю Кв и нижнюю Кн контрольные границы и строим диаграмму (рис. 4.2).

Полученную диаграмму редактируем с помощью контекстного меню - подписываем оси Работа с диаграммами/ Макет / Подписи/ название осей.

Наносим обозначения контрольных границ с помощью инструмента Надпись панели инструментов Работа с диаграммами/ Макет/Вставить/ Надпись.

Рис. 4.2. -карта - контрольная карта процесса дублирования

Далее рассчитываем данные для построения контрольной карты средних квадратических отклонений (s-карты).

Для удобства скопируем исходные данные в ячейку В30F49. В ячейках G4 рассчитываем среднее квадратическое отклонение выборки по формуле: =СТАНДОТКЛОН(В30:F30) и копируем полученную формулу в диапазон G31: G49.

В ячейке H30 рассчитываем среднее по СКО выборок по формуле: =СРЗНАЧ(G30: G49), и после указания абсолютной адресации, копируем формулу в диапазон H31: H49 – это середина поля допуска.

В ячейке I30 рассчитываем верхнюю контрольную границу по формуле: =H30*КОРЕНЬ(ХИ2ОБР(1-0,0027/2;4)/КОРЕНЬ(4) и копируем значение ячейки I30 в диапазон I31: I49.

В ячейке J30 рассчитываем нижнюю контрольную границу по формуле: =H30*КОРЕНЬ(ХИ2ОБР(0,0027/2;4)/КОРЕНЬ(4) и копируем содержимое ячейки в диапазон J31: J49.

Полученная электронная таблица s-карты представлена в (табл. 4.5), а графическое изображение контрольной s-карты показано на рис. 4.3.

Таблица 4.5. Таблица для построения s-карты

Номер подгруппы выборки	s		Кн	Кв
1	0,350714	0,441288	0,101481	1,316505
2	0,273861	0,441	0,101414	1,315645
3	0,570088	0,441	0,101414	1,315645
4	0,460435	0,441	0,101414	1,315645
5	0,476445	0,441	0,101414	1,315645
6	0,339116	0,441	0,101414	1,315645
7	0,350714	0,441	0,101414	1,315645
8	0,273861	0,441	0,101414	1,315645
9	0,570088	0,441	0,101414	1,315645
10	0,460435	0,441	0,101414	1,315645
11	0,476445	0,441	0,101414	1,315645
12	0,56745	0,441	0,101414	1,315645
13	0,612372	0,441	0,101414	1,315645
14	0,273861	0,441	0,101414	1,315645
15	0,570088	0,441	0,101414	1,315645
16	0,497996	0,441	0,101414	1,315645
17	0,476445	0,441	0,101414	1,315645
18	0,339116	0,441	0,101414	1,315645
19	0,612372	0,441	0,101414	1,315645
20	0,273861	0,441	0,101414	1,315645

По расчетных значениях строим -карту.

Чтобы получить из двух построенных карт единый объект, соединяем их по длине, например, прижав к левому краю электронной таблицы, или располагая диаграммы одна под другой.

Затем одновременно выделяем щелчками левой кнопкой мыши на каждой диаграмме при нажатой клавише Shift и группируем таблицы командой Группировать, вызываемого из Данные/Структура/Группировать.

Диаграммы группировать командой Работа с диаграммами / Формат / Упорядочить / Группировать.

(в Еxsel 2003 – в панели инструментов Рисование).

Полученная контрольная -карта показана на рис. 4.4.

Рис. 4.3. -карта - контрольная карта процесса дублирования

Анализ контрольной карты показывает, что рассеяние прочности клеевого соединения приемлемое, и по рассеянию процесс стабильный (оборудование настроено достаточно точно), поскольку на s-карте нет показаний разлаженности процесса.

Рис. 4.4. -карта - контрольная карта процесса дублирования