Построение диаграммы разброса в программе excel

Цель работы: ознакомиться с методикой оценки связей между двумя и более показателями и построения диаграммы разброса в программе Excel.

Задание: 1. Определить вид корреляционной связи между двумя переменными.

2. Построить диаграмму разброса в программе Excel.

Основные сведения

Диаграмма разброса (рассеяния) показывает взаимосвязь между двумя видами связанных данных и подтверждает их зависимость. Такими двумя видами данных могут быть характеристика качества и фактор, влияющий на нее, две разные характеристики качества одной продукции, два фактора, влияющих на одну характеристику качества, и т. д.

Для построения диаграммы рассеяния требуется не менее 30 пар данных (x, y).

Этапы построения диаграммы разброса:

1. Собрать парные данные (x, y), между которыми необходимо исследовать зависимость.

2. Найти минимальное и максимальное значения для x и y. Выбрать шкалу для горизонтальной и вертикальной осей так, чтобы длины рабочих частей осей x и y были приблизительно равны.

3. На диаграмму наносят точки (x, y), название диаграммы, интервал времени, число пар данных, названия осей, ФИО, должность исполнителя, и т. д.

Точки, которые далеко отстоят от основной группы распределения точек, является выбросами, и их исключают.

Возможны различные варианты скоплений точек. Для установления силы связи необходимо вычислить коэффициент корреляции r по формуле:

где n – число пар данных;

x_i, y_i - собранные статистические данные;

, - средние арифметические значения x и y;

r – коэффициент корреляции (множественный R ).

Коэффициент корреляции r используют только при линейной связи между величинами. Значение r находится в пределах от -1 до +1. Если r по модулю в диапазоне от 0,7 до 1, то проявляется сильная связь между рядами данных. Если коэффициент корреляции по модулю меньше 0,7, но больше 0,5 – говорят о связи средней силы; меньше 0,5 – говорят о слабой связи х и у. Если r, близко к нулю, корреляция слабая, а при нуле - отсутствует.

Можно оценить вероятность коэффициента корреляции m_r. Для этого вычисляют его среднюю ошибку по формуле

При r/m_r > 3 коэффициент корреляции считается достоверным, то есть связь доказана. При r/m_r <3 связь недостоверна, то есть, не доказана, а коэффициент корреляции незначим.

Пример 3.1. По экспериментальным данным (табл. 3.1), где: y - разрывное усилие, даН, и x - толщину ткани, см. Необходимо оценить уровень связи между этими показателями качества ткани, построить диаграмму рассеяния, рассчитать коэффициент корреляции оценить достоверность коэффициента корреляции.

В пакете Анализ данных инструмент Корреляция используется для количественной оценки взаимосвязи между двумя диапазонами данных, представленных в безразмерном виде. Коэффициент корреляции выборки представляет собой ковариацию двух наборов данных, деленную на произведение их стандартных отклонений.

Таблица 3.1. Экспериментальные данные

№	1	2	3	4	5	6	7	8	9	10
X	0,20	0,19	0,28	0,26	0,23	0,21	0,24	0,26	0,28	0,25
Y	64	65	69	69	66	65	67	67	70	68
№	11	12	13	14	15	16	17	18	19	20
X	0.25	0.22	0.18	0.26	0.17	0.30	0.19	0.25	0.29	0.27
Y	67	66	63	68	62	70	64	68	69	68
№	21	22	23	24	25	26	27	28	29	30
X	0,20	0,19	0,29	0,31	0,24	0,22	0,27	0,23	0,25	0,17
Y	63	66	70	72	66	65	69	65	69	61

Алгоритм действий следующий:

Формируют таблицу исходных данных в программе Excel. В ячейки А1 внести Х и В1- У.

Далее в ячейки А2:А31 располагаем значения Х. В ячейки В2:В31- значения У.

Открыть пакет Данные / Анализ / Анализ данных/ Корреляция / ОК.

Входной интервал: $А$1: $В$31 (или выделить диапазон данных ХУ).

Поставить галочку: метка в первой строке.

Выходной интервал: $D$1.

Нажать кнопку ОК.

Excel представит результаты решения в виде (табл. 3.2).

Таблица 3.2. Данные связи двух переменных Х и У (данные Корреляции)

	Столбец Х	Столбец У
Столбец Х	1
Столбец У	0,683269863	1

Полученные результаты свидетельствуют о сильной связи между данными х и у , т.к. коэффициент корреляции r ≈0,7.

Чтобы построить диаграмму разброса и получить его статистические характеристики воспользуемся инструментом Регрессия. Этот инструмент используется для анализа воздействия на зависимую переменную у одного или несколько независимых переменных х.

Алгоритм действий следующий:

Открыть пакет Данные / Анализ / Анализ данных / Регрессия / ОК.

Входной интервал У: $А$1: $А$31 (или выделить диапазон данных У).

Входной интервал Х: $В$1: $В$31 (или выделить диапазон данных Х).

Поставить галочки: константа-ноль, метка, уровень надежности (95%), график подбора, график нормальной вероятности.

Выходной интервал: $Е$6. Нажать кнопку ОК.

Excel представит результаты решения в виде (табл. 3.3 и 3.4, рис. 3.1 и 3.2).

Таблица 3.3. Данные регрессионной статистики

связи толщины и прочности ткани

Регрессионная статистика
Множественный R (коэффициент корреляции)	0,683269863
R-квадрат	0,466857706
Нормированный R-квадрат	0,44781691
Стандартная ошибка	1,972317081
Наблюдения	30

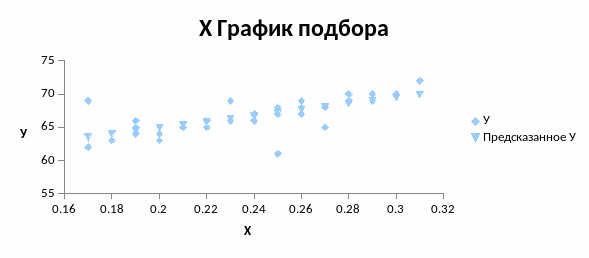
Рис. 3.1. Диаграмма разброса парных данных двух переменных Х и У

Таблица 3.4. Статистические данные дисперсионного анализа

связи толщины и прочности ткани

Дисперсионный анализ
	df	SS - суммы квадратов разностей	MS – оценки дисперсий	F –Расчетное значение критерия Фишера	Значимость F (табличное)
Регрес-сия	1	95,37902934	95,37902934	24,51881217	3,16536 α=E=0,5
Остаток	28	108,9209707	3,890034667
Итого	29	204,3

Рис. 3.2. График нормального распределения взаимосвязанных парных данных

Учитывая, что расчетное значение коэффициента Фишера больше чем табличное (табл. 3.4), то можно с 95 % уверенность утверждать, что прочность ткани зависит от её толщины, а коэффициенты корреляции значимы.

График нормального распределения (рис. 3.2) позволяет оценить сорт и качество ткани. График свидетельствует, что более 20% проб имеют стабильные значения, многократно повторяющиеся, что свидетельствует о высоком качестве ткани.

Персентиль – рассчитывается для каждого значения У, как сумма предшествующего вычисленного значения персентиля и h=(100% / наблюдения).

Начальное и конечное значение персентиля рассчитывается как (0+ h/2) и (100- h/2), соответственно.