МИНИСТЕРСТВО ОБРАЗОВАНИя И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ДИЗАЙНА И ТЕХНОЛОГИИ»

(ФГБОУ ВПО «МГУДТ»)

СТАТИСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ

И УПРАВЛЕНИЯ КАЧЕСТВОМ. Часть 1.

Методические указания

Учебно-методический комплекс

по направлению подготовки 270301Стандартизация и метрология

Составитель: Бесшапошникова В.И., проф., д. т. н.

Москва

МГУДТ 2016

УДК [67:001](075)

Б 53

Б 53 Статистические методы управления качеством, часть 1 : Методические указания /Сост. Бесшапошникова В. И. – М. : МГУДТ, 2016. - 64 с.

Рецензент: д.т.н., проф. Родэ С.В.. (ФГБОУ ВПО «МГУДТ»)

Методические указания предназначены для обучающихся по направлению подготовки 27.03.01 – Стандартизация и метрология всех форм обучения и будут использованы при изучении дисциплины «Статистические методы контроля и управления качеством».

Методические указания содержат 7 практических работ по 4 основным темам дисциплины. В каждой работе изложены краткие теоретические сведения, рассмотрены примеры и подготовлены задания для самостоятельной работы, дана методика и порядок проведения работы, в том числе с применением программного обеспечения ПК.

УДК [67:001](075)

Подготовлено к печати на кафедре «Материаловедение»

Печатается в авторской редакции

		СОДЕРЖАНИЕ		стр.
1.	Лабораторная работа №1 Статистические методы контроля качества в программе Excel. Выборка.……………………………………………………………..		4
2.	Лабораторная работа №2 Статистические методы контроля качества в программе Еxcel. Карты Парето ………………………………………..……………….		11
3.	Лабораторная работа №3 Построение диаграммы разброса в программе Excel .……………		16
4.	Лабораторная работа №4 Контрольные карты (карты Шухарта) по количественным признакам в программе Excel ..…………………………….……...		22
5.	Лабораторная работа №5 Контрольные карты (карты Шухарта) по качественным признакам в программе Excel ..…………………………………...		38
6.	Лабораторная работа №6 Статистические методы оценки погрешности измерений и характеристик приборов …………………………..………………..		45
7	Лабораторная работа №7 Статистические методы оценки погрешности измерений и характеристик двух сравниваемых приборов		54
	Список рекомендуемой литературы……………………………….		60
	Приложения…………………………………………………………..		61

Лабораторная работа №1

Статистические методы контроля качества в программе excel. Выборка.

Цель работы: Приобретение навыков обрабатывать статистические данные оценки качества продукции на ПК в программе Excel.

Задание: 1. Изучить математический редактор программы Excel.

2. Выполнить задание статистической обработки данных на ПК. Произвести выборку данных.

Основные сведения

Словом «совокупность» (статистическая совокупность) принято в статистике обозначать множество объектов, из которых извлекается выборка. Она называется генеральной совокупностью.

Генеральную совокупность можно изучать путем сплошного наблюдения ее объектов (элементов) или некоторой части, которую называют выборочной совокупностью или просто выборкой.

Количество объектов генеральной или выборочной совокупности называют объемом.

Сплошное наблюдение применяют тогда, когда объем небольшой, или наблюдение имеет основной задачей полный учет всех элементов совокупности, составляющих изучаемое явление. Например, при инвентаризации — полный учет всех материальных средств на балансе предприятия.

Выборочная совокупность в одних случаях используется для оценки среднего значения некоторого признака генеральной совокупности, а в других — доли членов генеральной совокупности с другим признаком. В первом случае это может быть средняя заработная плата, средняя продолжительность жизни и т.д., а во втором — доля стандартных деталей, удельный вес отличников в вузе и т.д.

Чтобы по данным выборки можно было с уверенностью судить об интересующем признаке генеральной совокупности, выборка должна быть представительной (репрезентативной).

Выборка является репрезентативной, если она образована случайно. Существуют различные способы отбора. В зависимости от способа отбора различают выборки следующих типов: собственно случайная выборка и механическая выборка.

Образование собственно случайных выборок. Если выборку производят из массы изделий, то после тщательного перемешивания следует брать объекты случайно, т.е. так, чтобы все они имели одинаковую вероятность попасть в выборку. Часто для образования случайной выборки элементы генеральной совокупности предварительно нумеруют, а каждый номер записывают на отдельную карточку. В результате получают пачку карточек, число которых совпадает с объемом генеральной совокупности. После тщательного перемешивания из этой пачки берут по одной карточке. Объект, имеющий одинаковый номер с карточкой, считается попавшим в выборку.

При большом объеме генеральной совокупности пользуются таблицами случайных чисел, в которых числа расположены в случайном порядке. Для того чтобы отобрать, например, 50 объектов из пронумерованной генеральной совокупности, открывают любую страницу таблицы случайных чисел и выписывают подряд 50 чисел; в выборку попадают те объекты, номера которых совпадают со случайными числами. Если случайное число таблицы окажется больше объема генеральной совокупности, то такое число пропускают.

При механическом способе образования выборочной совокупности, подлежащие обследованию элементы генеральной совокупности, отбирают через определенный интервал. Так, например, если выборка должна составить 50% генеральной совокупности, то отбирают каждый второй элемент генеральной совокупности. Если выборка 10%-я, то отбирают каждый 10-й ее элемент и т.д.

Выполняют выборку на ПК в программе Excel. Пакет Анализ/Анализ данных инструмент Выборка используется для создания выборки из генеральной совокупности данных. Инструмент Выборка предлагает два способа формирования выборки.

1. Периодический. Это механический способ формирования выборки. В качестве параметра Excel предлагает Период — периодический интервал, в соответствии с которым будет произведена выборка. Входное значение, номер которого совпадает с номером, заданным в поле Период, и каждое последующее с номером, кратным периоду, будет скопировано в выходной столбец. Процесс создания выборки прекратится при достижении конца входного диапазона.

2. Случайный. Это собственно случайный способ формирования выборки. В качестве параметра Excel предлагает Число выборок — число случайных значений (объем выборки), которые необходимо разместить в выходном столбце. Позиция каждой извлекаемой переменной во входном диапазоне выбирается случайным образом.

Пример 1.1. Для оценки качества партии шелковых тканей из 20 рулонов провели испытание 200 проб, определяя прочность при растяжении до разрыва ткани. Результаты представлены в табл. 1.1. Провести статистическую обработку данных на ПК и оценить качество партии продукции.

Решение 1. Сформировать 2%-ю выборку данных испытания проб (табл. 1.1).

Таблица 1.1. Совокупность данных прочности шелковой ткани

Номер	А	В	С	D	E	F	G	H	I	J
1	25	24	25	24	24	24	24	23	23	25
2	25,5	24,3	25,2	24,1	24,6	24,4	24,7	23,8	23,9	25,3
3	26	24,6	25,4	24,2	25,2	24,8	25,4	24,6	24,8	25,6
4	26,5	24,9	25,6	24,3	25,8	25,2	26,1	25,4	25,7	25,9
5	27	25,2	25,8	24,4	26,4	25,6	26,8	26,2	26,6	26,2
6	27,5	25,5	26	24,5	27	26	27,5	27	27,5	26,5
7	28	25,8	26,2	24,6	27,6	26,4	28,2	27,8	28,4	26,8
8	28,5	26,1	26,4	24,7	28,2	26,8	28,9	28,6	29,3	27,1
9	29	26,4	26,6	24,8	28,8	27,2	29,6	29,4	30,2	27,4
10	29,5	26,7	26,8	24,9	29,4	27,6	30,3	30,2	31,1	27,7
11	25	24	25	24	24	24	24	23	23	25
12	25,5	24,3	25,2	24,1	24,6	24,4	24,7	23,8	23,9	25,3
13	26	24,6	25,4	24,2	25,2	24,8	25,4	24,6	24,8	25,6
14	26,5	24,9	25,6	24,3	25,8	25,2	26,1	25,4	25,7	25,9
15	27	25,2	25,8	24,4	26,4	25,6	26,8	26,2	26,6	26,2
16	27,5	25,5	26	24,5	27	26	27,5	27	27,5	26,5
17	28	25,8	26,2	24,6	27,6	26,4	28,2	27,8	28,4	26,8
18	28,5	26,1	26,4	24,7	28,2	26,8	28,9	28,6	29,3	27,1
19	29	26,4	26,6	24,8	28,8	27,2	29,6	29,4	30,2	27,4
20	29,5	26,7	26,8	24,9	29,4	27,6	30,3	30,2	31,1	27,7

Алгоритм действий следующий.

Откройте лист Excel

В ячейки А1:А200 занесите данные таблицы 1.1.

Офис/параметры/надстройка/Пакет анализа/Перейти.

В открывшемся окне доступные надстройки установить флажок Пакет анализа и нажать кнопку ОК. Установленный пакет анализа доступен на ленте во вкладке Данные в окне Анализ /пакет Анализ данных. Пакет Анализ данных содержит 19 команд, найдите инструмент Выборка и нажмите ОК. В результате появится диалоговое окно выбранного режима для выбора параметров Выборки:

Входной интервал — $А$1: $А$200

Метод выборки —Случайный

Число выборок: 100

Выходной интервал - $В$1

ОК.

Результат решения будет представлен в виде (табл. 1.2):

Таблица 1.2.

Номер опыта	А	В	С	D	E	F	G	H	I	J
1	24	26,4	24,4	28,4	29,3	27,5	26	25,4	25	27,5
2	25,4	25,2	24	26,7	25,4	29,5	26	27,6	28	25,4
3	27,5	26,5	28	26,8	26,5	27,5	26,8	24,3	26,8	26,2
4	23	31,1	24	26,8	25,2	25	25	25	26,8	24,8
5	26,8	27,5	26	26,8	26,4	26	25,9	23	24,3	27
6	27,7	26,7	24,1	24,8	24	30,2	29,4	26,1	25	25
7	26	26,8	28,9	25,5	29,4	27,5	25,5	24	26,4	27,6
8	24	24	29,4	24,6	25,2	24,2	24,5	26,8	27,2	27,2
9	26	24,6	25,8	27,8	29,5	27,8	24,3	24	27,5	26,8
10	26,7	24	24,4	24,8	25	26,6	27,1	27,5	24,6	31,1

Примечание. Результат решения (табл. 1.2) будет размещен в диапазоне $В$1:$В$100 (в один столбец), однако для наглядности примера полученная выборка объемом 100 разбита на 10 равных частей.

Решение 2. Найти среднее арифметическое, дисперсию, стандартное отклонение и другие статистические характеристики значений результатов испытания по данным выборки (табл. 1.2).

Алгоритм действий следующий.

В таблице лист Excel данные выборки, расположены в столбце В1:В100.

Анализ данных можно проводить как с помощью специализированных статистических функций, так и с помощью пакета Анализа данных.

Выполните команды: Данные/Анализ/Анализ данных.

В появившемся списке Инструменты анализа выбрать строку Описательная статистика.

В появившемся диалоговом окне в поле Входной интервал укажите входной диапазон В1:В100.

Установите флажок Группирование в команду по столбцам.

Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон - ячейку В101.

Установите флажок в поле Итоговая статистика. Уровень надежности задайте 95%. Нажмите ОК.

В результате анализа получите в диапазоне В101:В116 наименования основных показателей описательной статистики и их значения в С103:С116 (табл. 1.3).

Таблица 1.3. Статистические показатели анализа данных

испытания проб шелковой ткани

Столбец1
Среднее	26,24
Стандартная ошибка	0,174362
Медиана	26,15
Мода	24
Стандартное отклонение	1,743618
Дисперсия выборки	3,040202
Эксцесс	0,076475
Асимметричность	0,566625
Интервал (размах выборки)	8,1
Минимум	23
Максимум	31,1
Сумма	2624
Счет	100
Уровень надежности(95,0%)	0,345972

Результаты в (табл. 1.3) были получены с помощью инструмента Описательная статистика и вычисления по формулам:

• среднее (статистическая оценка математического ожидания)

• стандартная ошибка (среднего)

• медиана (Me) - значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности;

• мода (Мо) — значение изучаемого признака, повторяющегося с наибольшей частотой;

• дисперсия выборки

• стандартное отклонение (среднее квадратическое отклонение)

• Эксцесс

• Асимметричность (асимметрия)

• Интервал (размах выборки) R = х_тах - x_min;

• Минимальное значение выборки x_min;

• Максимальное значение выборки х_тах;

• Сумма всех значений выборки.

• Объем выборки n;

• наибольшее значение признака, имеющее разность с порядком х_тах k единиц;

• наименьшее значение признака, имеющее разность с порядком x_min k единиц;

• уровень надежности (предельная ошибка выборки)

;

где t — параметр распределения Стьюдента, определяемый по уровню значимости α = 1-р и числу степеней свободы k = п - 1.

Доверительный интервал (Интервал) находился по формуле:

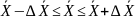
где – средняя арифметическая выборки (среднее);

- предельная ошибка выборки (показатель уровня надежности в 95%).

Коэффициент ковариации (корреляции) рассчитывается по формуле

где k- коэффициент ковариации (корреляции), σ – стандартное отклонение по выборке.

Коэффициент ковариации значительно меньше 50%, что свидетельствует о небольших отклонениях показателей разрывной нагрузки проб в анализируемой партии шелковых тканей.