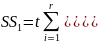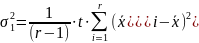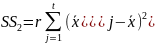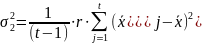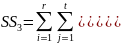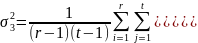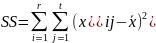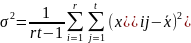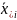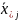Самостоятельная работа по теме 3.1

Задание 3.1. Имеется пять партий обуви. Из каждой партии отобрано по пять образцов и проведены испытания на определение величины разрывной нагрузки кожи. Результаты испытаний приведены в табл. 3.6.

Таблица 3.6

Номер партии, т	Разрывная нагрузка, даН, п
1	230	240	210	215	205
2	200	202	240	195	230
3	230	220	209	196	208
4	220	238	194	230	180
5	209	232	240	224	217

Требуется выяснить, существенно ли влияние различных партий сырья на величину разрывной нагрузки обуви.

Задание 3.2. Имеется четыре партии детской одежды. Из каждой партии отобрано по пять образцов и проведены испытания на определение гигроскопичности. Результаты испытаний приведены в табл. 3.7.

Таблица 3.7

Номер партии, т	Гигроскопичность, %, п
1	16,5	13,8	14,5	16,8	17,2
2	14,9	16,2	16,8	15,9	17,6
3	15,5	15,6	16,5	16,1	17,8
4	15,7	16,1	16,7	17,3	15,2

Требуется выяснить, существенно ли влияние различных партий сырья на величину гигроскопичности одежды.

3.2. Двухфакторный дисперсионный анализ

Если на исследуемый признак влияют несколько факторов одновременно, то имеет место многофакторный дисперсионный анализ, который имеет свои особенности, так как имеет место дополнительное влияние взаимодействия между факторами.

Рассмотрим на примере задачу оценки влияния двух одновременно действующих факторов. Предположим, что имеется несколько однотипных прессов, формования деталей обуви, и несколько видов сырья. Требуется выяснить, значимо ли влияние различных прессов и качество сырья в партиях на качество обрабатываемых деталей обуви. Это типичная задача двухфакторного дисперсионного анализа.

Считаем, что предпосылки дисперсионного анализа выполнены. Пусть фактор А - влияние настройки прессов, фактор В - влияние качества сырья. Имеем r станков, следовательно, r уровней фактора A, t партий сырья, следовательно, t уровней фактора В. Матрицу наблюдений представим в виде (табл. 3.8).

Таблица 3.8

Пресса, i	Партии сырья, j
	B1	B2	…	BJ	…	Bt	i*
A1	x11	x12	…	…	…	x1t	1*
A2	x21	x22	…	…	…	x2t	2*
…	…	…	…	…	…	…	…
Ai	…	…	…	xij	…	…	…
…	…	…	…	…	…	…	…
Ar	xr1	xr2	…	…	…	xrt	r*
*j	*1	*2	…	…	…	*t

Пересечение i-го уровня фактора A с j-м уровнем фактора В образует ij-ю ячейку, в которую записывают наблюдения, полученные при одновременном исследовании факторов А и В на i-м и j-м уровнях.

Для простоты можно предположить, что имеем в ячейке только одно наблюдение x_ij. Предположим также, что между факторами А и В нет взаимодействия и что на i-м уровне фактора А наблюдения имеют среднюю β_iA, а на j-м уровне фактора В наблюдения - среднюю β_jB. Тогда одно наблюдение можно представить в виде

x_ij = µ + γ_i + γ_j +e_ij (3.3)

где µ - общая средняя; γ_i - эффект, обусловленный влиянием i-го уровня фактора А; γ_j — эффект, обусловленный влиянием j-го уровня фактора В; e_ij - вариация результатов внутри отдельной ячейки (в случае одного наблюдения вариация равна нулю).

Оценками µ, β_iA , β_jB - являются соответственно:

общая средняя

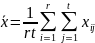
и средние по уровням

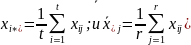
В двухфакторном дисперсионном анализе общая сумма квадратов отклонений от общей средней раскладывается согласно формуле (3.3) на три части: часть общей суммы квадратов, обусловленную влиянием фактора А, часть, обусловленную влиянием фактора В, и часть, обусловленную влиянием факторов взаимодействия АВ. Сумма квадратов отклонений (табл. 3.9) рассчитывается по формуле:

SS=SS₁+SS₂+SS₃,

где SS₁, представляет собой сумму квадратов разностей между средними по строкам и общим средним и характеризует изменение признака по фактору A.

SS₂ представляет собой сумму квадратов разностей между средними по столбцам и общим средним и характеризует изменение признака по фактору В.

SS₃ называется остаточной суммой квадратов и характеризует влияние факторов взаимодействия.

SS называется общей или полной суммой квадратов отклонений отдельных наблюдений от общей средней.

Таблица 3.9

Компоненты дисперсии	Сумма квадратов	Оценка дисперсии
Между средними по строкам
Между средними по столбцам
Остаточная
Полная (общая)

В двухфакторном анализе для выяснения значимости влияния факторов А и В на исследуемый признак сравнивают дисперсии по факторам с остаточной дисперсией. Оценим дисперсии по формулам (табл. 3.9).

Для оценки существенности влияния факторов А и В и их взаимодействия АВ достаточно проверить нулевую гипотезу H₀.

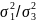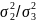Для этого вычисляют критерий Фишера F₁ = , с числом степеней свободы k₁= r - 1 и k₂ = (r-1)(t - 1) и F₂ = , с числом степеней свободы k₁= t - 1 и k₂ = (r-1)(t - 1).

Затем по таблице F-распределения (см. таблицу распределения критерия Фишера) для уровня значимости α находят критическое значение F_кр. Если F_1,2 > F_кр то нулевая гипотеза отвергается.

При F_1,2 < F_кр нет основания отвергать нулевую гипотезу.

Сравнение отношений дисперсии между средними по строкам и столбцам с остаточной дисперсией, т.е. отношений и по их величине судят, насколько сильно проявляется влияние факторов на исследуемый объект.

Рассмотрим пример 3.2. В раскройном цехе работает три закройщика. Лекала конструкции одежды разрабатывали два конструктора. Требуется выяснить, значимо ли влияние качества конструкции лекал и качество работы закройщиков на качество готовой одежды. Количество настилов тканей раскроенных каждым закройщиком по лекалам конструкторов представлено в (табл. 3.10).

Таблица 3.10. Матрица наблюдений

	В1	В2	В3
А1	1	2	3	2
А2	5	6	10	7
	3	4	6,5	4,5

Решение.

Пусть фактор А (А₁ и А₂) – влияние работы конструкторов, а фактор В (В₁, В₂, В₃) влияние качества работы закройщиков. Имеем r = 2, t = 3, п = rv = 6.

В матрице наблюдений (табл. 3.10) нижняя строка содержит средние значения по столбцам, а в правом крайнем столбце приведены средние значения по строкам, т.е. по уровням факторов. Общее среднее = 4,5.

По формулам (табл. 3.9) вычислим суммы квадратов:

SS₁ = 37,5; SS₂ = 13; SS₃ = 3; SS= 53,5.

Рассчитаем оценки дисперсий:

= 37,5/1 = 37,5; = 13/2 = 6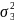,5; = 3/(1 ∙ 2) = 1,5;

σ² = 53,5/(2∙3- 1) = 10,7.

Вычисляем F_a и F_В: F_А = =37,5/1,5=25

и F_В = =6,5/1,5=4,3

Для уровня значимости α = 0,05 и к₂ = 2, к₁ = 1 степеней свободы по таблице F-распределения (см. приложения) находим значения F_кр: F_крА=18,51 и F_крВ=19,0

Сравнивая табличные значения с вычисленными, имеем:

F_a > F_KрА; F_B < F_крB.

Полученные результаты позволяют сделать следующие выводы:

1 - нулевая гипотеза о равенстве средних по строкам не подтверждается, т.е. влияние фактора А на исследуемый признак значимо;

2 - нулевая гипотеза о равенстве средних по столбцам не опровергается, т.е. влияние фактора В на исследуемый признак незначимо.

Выполним расчеты в программе Excel.

В пакете Анализ данных инструмент Двухфакторный дисперсионный анализ без повторений представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности)

Алгоритм действий следующий.

Формируем в Excel таблицу исходных данных:

	A	B	C	D
1		В1	В2	В3
2	А1	1	2	3
3	А2	5	6	10

Сервис / Анализ данных / Двухфакторный дисперсионный анализ без повторений / ОК.

Входной интервал: $A$1:$D$3.

Поставить флажок в поле Метки.

Альфа: 0,05.

Выходной интервал: $A$6. ОК.

Excel представит результаты решения в следующем виде (табл. 3.11).

Таблица 3.11. Результаты Двухфакторного дисперсионного анализа без повторений

Двухфакторный дисперсионный анализ без повторений
ИТОГИ	Счет	Сумма	Среднее	Дисперсия
A1	3	6	2	1
A2	3	21	7	7
B1	2	6	3	8
B2	2	8	4	8
B3	2	13	6,5	24,5
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Зна-чение	F крити-ческое
Строки	37,5	1	37,5	25	0,03775	18,51282
Столбцы	13	2	6,5	4,33333	0,1875	19
Погрешность	3	2	1,5
Итого	53,5	5

Результаты представлены в виде двух таблиц:

1) Итоги. В данной таблице представлены промежуточные данные расчетов для каждой строки и столбца: число элементов (счет), суммы величин (сумма), среднее арифметическое величин (среднее), дисперсия величин (дисперсия);

2) Дисперсионный анализ. В данной таблице представлены соб­ственно результаты дисперсионного анализа: компоненты дисперсии (источник вариации), суммы квадратов (SS), число степеней свободы (df), средний квадрат (MS), статистика F_B (F), вероятность значимости (Р-значение), статистика F (F критическое).

Если выборочное значение статистики (F) оказалось меньше критического (F критическое) то нулевая гипотеза - принимается, в противном случае – отвергается.

Сравнивая табличные значения критерия Фишера с вычисленными, имеем:

F_a > F_KрА; F_B < F_крB.

Таким образом, нулевая гипотеза о равенстве средних по строкам не подтверждается, т.е. влияние фактора А значимо, т.е. качество работы конструктора оказывает непосредственное влияние на качество изделия;

Влияние фактора В незначимо, т.е. работа закройщика не оказывает значительного влияния на качество одежды.