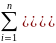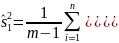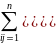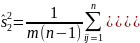Самостоятельная работа по теме 2.3

Задача 2.7. Проведено 100 опытов оценки качества 7 партий тканей. Используя критерий 𝜒² при уровне значимости α = 0,05, необходимо проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки объема п=100 из этой генеральной совокупности. Выборка представлена интервальным рядом:

Интервал	5-10	10-15	15-20	20-25	25-30	30-35	40-45
Частота, тi	6	7	9	30	25	15	8

Сделайте выводы по полученным данным.

Задача 2.8. Проведено 200 опытов оценки качества 6 партий обуви. Используя критерий 𝜒² при уровне значимости α = 0,05, необходимо проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки объема п=200 из этой генеральной совокупности. Выборка представлена интервальным рядом:

Интервал	5-13	13-21	21-29	29-37	37-45	45-53
Частота, тi	5	35	65	50	38	7

Сделайте выводы по полученным данным.

Практическая работа №3 факторный анализ. Дисперсионный анализ

Дисперсионный анализ - это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния. В дисперсионном анализе исследуется влияние одного или нескольких качественных факторов на количественный результативный признак. Суть анализа заключается в разложении общей вариации случайной величины на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Этот метод находит применение в различных областях науки и техники.

Факторами обычно называют внешние условия, влияющие на изучаемый объект. Например: температура, давление, время, тип оборудования и т.п. Действие фактора на объект должно быть значительно и должно поддаваться проверке. Факторы могут варьировать, благодаря чему можно исследовать влияние контролируемого фактора на объект. При этом фактор варьирует на разных уровнях или имеет несколько уровней. В зависимости от количества факторов, включенных в анализ, различают: однофакторный, двухфакторный анализ и многофакторный анализ.

Для проведения дисперсионного анализа необходимо соблюдать следующие условия:

• результаты наблюдений должны быть независимыми случайными величинами,

• иметь нормальное распределение

• иметь одинаковую дисперсию.

Только в этом случае можно оценить значимость полученных оценок дисперсий и математических ожиданий и построить доверительные интервалы.

3.1. Однофакторный дисперсионный анализ

Предположим, что на автоматической линии несколько станков параллельно выполняют одинаковую операцию. Для правильного планирования последующей обработки важно знать, насколько однотипны средние размеры деталей, получаемые на параллельно работающих станках. Здесь имеет место лишь один фактор, влияющий на размер деталей, это станки, на которых они изготовляются. Необходимо выяснить, насколько существенно влияние этого фактора на размеры деталей. Предположим, что совокупности размеров деталей, изготовленных на каждом станке, имеют нормальное распределение и равные дисперсии.

Имеем т станков, следовательно, т совокупностей или уровней, на которых произведено n₁, n₂,..., п_т наблюдений. Для простоты рассуждений предположим, что n₁=n₂=…=п_т. Размеры деталей, составляющие n_i наблюдений на i-м уровне, обозначим х_i1,х_i2,..., x_in. Тогда все наблюдения можно представить в виде таблицы, которая называется матрицей наблюдений (табл. 3.1).

Таблица 3.1

Уровни	Результаты наблюдений
	1	2	…	j	…	n
1	x11	x12	…	x1j	…	x1n
2	x21	x22	…	x2j	…	x2n
3	x31	x32	…	x3j	…	x3n
…	…	…	…	…	…	…
i	xi1	xi2	…	xij	…	xin
…	…	…	…	…	…	…
m	xm1	xm2	…	xmj	…	xmn

Будем полагать, что для i-го уровня п наблюдений имеют среднюю β_i, равную сумме общей средней µ и вариации ее, обусловленной i-м уровнем фактора, т.е. β_i = µ + γ_i. Тогда одно наблюдение можно представить в следующем виде:

x_ij = µ + γ_i. +ε_ij= β_i +ε_ij (3.1)

где µ — общая средняя; γ_i — эффект, обусловленный i-м уровнем фактора; ε_ij — вариация результатов внутри отдельного уровня.

Член ε_ij характеризует влияние всех не учтенных моделью (3.1) факторов. Согласно обшей задаче дисперсионного анализа нужно оценить существенность влияния фактора γ на размеры деталей. Общую вариацию переменной x_ij можно разложить на части, одна из которых характеризует влияние фактора γ, другая — влияние неучтенных факторов. Для этого необходимо найти оценку общей средней µ и оценки средних по уровням β_i. Очевидно, что оценкой β является средняя арифметическая п наблюдений i-го уровня, т.е.

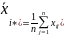
Звездочка в индексе при х означает, что наблюдения фиксированы на i-м уровне. Средняя арифметическая всей совокупности наблюдений является оценкой общей средней µ, т.е.

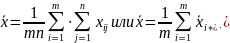
Найдем сумму квадратов отклонений x_ij от 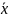, т.е.

Представим ее в виде (3.2)

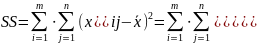
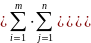
(3.2)

Причем =

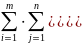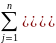
Но = 0, так как это есть сумма отклонений переменных одной совокупности от средней арифметической этой же совокупности, т.е. вся сумма равна нулю. Второй член суммы (3.2) запишем в виде:

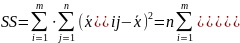
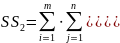
Или

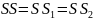
Слагаемое 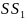является суммой квадратов разностей между средними уровней и средней всей совокупности наблюдений. Эта сумма называется суммой квадратов отклонений между группами и характеризует расхождение между уровнями. Величину , называют также рассеиванием по факторам, т.е. рассеиванием за счет исследуемого фактора.

Слагаемое 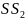является суммой квадратов разностей между отдельными наблюдениями и средней i-го уровня. Эта сумма назы­вается суммой квадратов отклонений внутри группы и характеризует расхождение между наблюдениями i-го уровня. Величину называют также остаточным рассеиванием, т.е. рассеиванием за счет неучтенных факторов.

Величину 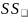называется общей или полной суммой квадратов отклонений отдельных наблюдений от общей средней .

Зная суммы квадратов SS, SS₁ и SS₂, можно оценить несмещенные оценки соответствующих дисперсий - общей, межгрупповой и внутригрупповой (таблица 3.2).

Если влияние всех уровней фактора γ одинаково, то 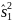и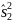 - оценки общей дисперсии.

Тогда для оценки существенности влияния фактора γ достаточно проверить нулевую гипотезу H₀: = .

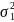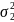Для этого вычисляют критерий Фишера F_B = 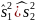, с числом степеней свободы k₁= т - 1 и k₂ = т(п - 1). Затем по таблице F-распределения (см. таблицу распределения критерия Фишера) для уровня значимости α находят критическое значение F_кр.

Таблица 3.2

Компоненты дисперсии	Сумма квадратов	Число степеней свободы k	Оценка дисперсии
Межгрупповая		т-1
Внутри-групповая		m(n - 1)
Полная (общая)		тп - 1

Если F_B > F_кр то нулевая гипотеза отвергается и делается заключение о существенном влиянии фактора γ.

При F_B < F_кр нет основания отвергать нулевую гипотезу и можно считать, что влияние фактора γ несущественно.

Сравнивая межгрупповую и остаточную дисперсии, по величине их отношения судят, насколько сильно проявляется влияние факторов.

Пример 3.1. Имеется четыре партии тканей для спецодежды. Из каждой партии отобрано по пять образцов и проведены испытания на определение величины разрывной нагрузки. Результаты испытаний приведены в табл. 3.3.

Таблица 3.3

Номер партии, т	Разрывная нагрузка, даН, п
1	200	140	170	145	165
2	190	150	210	150	150
3	230	190	200	190	200
4	150	170	150	170	180

Требуется выяснить, существенно ли влияние различных партий сырья на величину разрывной нагрузки.

Решение.

В данном случае т = 4, п = 5. Среднюю арифметическую каждой строки вычисляем по формуле

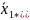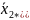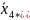Имеем: =(200+140+170+145+165)/5=164; =170; =202; = 164.

Найдем среднюю арифметическую всей совокупности:

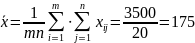
Вычислим величины, необходимые для построения табл. 3.4:

• сумму квадратов отклонений между группами SS₁, с k₁=т –1=

=4-1=3 степенями свободы:

• сумму квадратов отклонений внутри группы SS₂ с k₂ = тп – т= =20-4=16 степенями свободы:

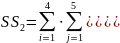
• полную сумму квадратов SS c k=mn-1=20-1=19 степенями свободы:

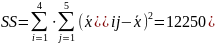
По найденным значениям оценим дисперсию, по формулам (табл. 3.2) составим (табл. 3.4) для рассматриваемого примера.

Таблица 3.4

Компоненты дисперсии	Суммы квадратов	Число степеней свободы	Оценка дисперсий
Межгрупповая	4980	3	1660,0
Внутригрупповая	7270	16	454,4
Полная	12250	19	644,7

Проведем статистический анализ по критерию Фишера. Вычислим F_B = =(4980• 1/3)/(7270 • 1/16) =1660/454,4= 3,65.

По таблице F-распределения (см. приложения) находим значение F_Kp при k₂ = 16 и k₁ = 3 степенях свободы и уровне значимости α = 0,01. Имеем F_Kp = 5,29.

Вычисленное значение F_B меньше табличного, поэтому можно утверждать, что нулевая гипотеза не отвергается, а это значит, что различие между тканями в партиях не влияет на величину разрывной нагрузки.

В пакете Анализ данных инструмент Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности. Рассмотрим работу пакета для проведения однофакторного дисперсионного анализа.

Решим пример 3.1, используя инструмент Однофакторный дисперсионный анализ.

Алгоритм действий следующий.

1. Формируем таблицу исходных данных:

	A	B	C	D	E	F
1	Номер партии, т	Разрывная нагрузка, п
2	1	200	140	170	145		165
3	2	190	150	210	150		150
4	3	230	190	200	190		200
5	4	150	170	150	170		180

2.Сервис /Анализ данных / Однофакторный дисперсионный анализ /ОК.

3. В диалоговое окно внести:

• Входной интервал: $A$2:$F$5.

• Группирование: по строкам.

• Поставить флажок в поле Метки в первом столбце.

• Альфа: 0,01.

• Выходной интервал: $A$8. ОК.

Excel представит результаты решения в виде двух таблиц, представленных в (табл. 3.5).

Таблица 3.5

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
1	5	820	164	567,5
2	5	850	170	800
3	5	1010	202	270
4	5	820	164	180
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	4980	3	1660	3,65337	0,035248	5,292214
Внутри групп	7270	16	454,3
Итого	12250	19

В первой части таблице (табл. 3.5) приводятся статистические характеристика для каждой партии тканей. Они представлены таблицей «ИТОГИ» - промежуточные данные расчетов для каждой партии (группы): число образцов (счет), суммы величин разрывной нагрузки (сумма), среднее арифметическое величин разрывной нагрузки (среднее), дисперсия величин разрывной нагрузки (дисперсия).

Во второй части (табл. 3.5) таблица «Дисперсионный анализ» - в которой представлены собственно результаты дисперсионного анализа: компоненты дисперсии (источник вариации), суммы квадратов (SS), число степеней свободы (df), средний квадрат (MS), статистика F_B (F), вероятность значимости (P-значение), статистика F_кр (F-критическое).

Вероятность значимости (P-значение) определяется так же, как при рассмотрении двухвыборочного F-теста для дисперсий.

Если выборочное значение статистики (F) оказалось меньше критического (F критическое) то нулевая гипотеза, что различие между тканями в партиях не влияет на величину разрывной нагрузки - принимается, в противном случае – отвергается.