Самостоятельная работа по теме 2.3

Задание 2.5. Имеется нормально распределенная совокупность из 200 данных испытания партии костюмной ткани на прочность со средним значением 72 даН. Сделайте случайную выборку 20 элементов из этой совокупности. Используя критерий 𝜒² (хи-квадрат), проверьте, действительно ли выборка сделана из нормально распределенной генеральной совокупности. Сделайте выводы по полученным данным.

Задание 2.6. Имеется нормально распределенная совокупность из 150 данных испытания партии шелковой ткани на усадку со средним значением 2,5% и стандартным отклонением 0,25. Сделайте случайную выборку 15 элементов из этой совокупности. Используя критерий 𝜒² (хи-квадрат), проверьте, действительно ли выборка сделана из нормально распределенной генеральной совокупности. Сделайте выводы по полученным данным.

Пример 2.4. Задачи с интервальным вариационным рядом.

Используя критерий 𝜒² при уровне значимости α = 0,05, необходимо проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки объема п=100 из этой генеральной совокупности. Выборка представлена интервальным рядом:

Интервал	3-8	8-13	13-18	18-23	23-28	28-33	33-38
Частота, тi	6	8	15	40	16	8	7

Решение.

1. Определяем статистические оценки параметров распределения по формулам и результаты заносим в таблицу 2.10:

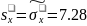
2. Вычисляем вероятность попадания нормальной случайной величины с параметрами и 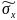в интервал, для этого используем функцию Лапласа, приняв х₁ = - , х_j = .

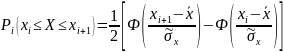
где

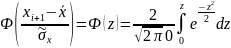
- функция Лапласа (см. таблицу «Значения функции Лапласа» приложения 2).

Составляем следующую расчетную таблицу 2.10:

Таблица 2.10. Статистические оценки параметров распределения

Интервал	3-8	8-13	13-18	18-23	23-28	28-33	33-38
Рi	0,0405	0,1045	0,2103	0,2687	0,2181	0,1124	0,0455
nPi	4,05	10,45	21,03	26,87	21,81	11,24	4,55

3. Вычисляем опытное значение критерия:

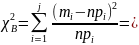13,46

и число степеней свободы k: = 7 - 2 - 1=4.

4. По таблице распределения 𝜒² (см. таблицу распределения Пирсона (𝜒²-распределение), приложение 3) определяем вероятность (можно использовать рассмотренную функцию ХИ2РАСП, см. пример 2.3.):

α = Р(Y> ) = 0,036.

Так как α < α_кр = 0,05, то гипотезу о нормальном распределении генеральной совокупности отвергаем.

Решим данный пример с использованием функции ХИ2ТЕСТ.

Алгоритм действий следующий.

1. Формируем рабочую таблицу 2.11 в программе Ехсеl, где будут производиться промежуточные расчеты:

Таблица 2.11

	A	B	C	D	E	F	G	H	I	J	K	L		N		M		O
1	Границы интервалов,хi,	3	8	8	13	13	18	18	23	23	28	28		33		33		38
2	Середины интервалов,	5,5		10,5		15,5		20,5		25,5			30,5				35,5
3	-	-15,2		-10,2		-5,2		-0,2		4,8			9,8				14,8
4		231,04		104,04		27,04		0,04		23,04			96.04				219,04
5	zi	-1376,97	-1,75	-1,75	-1,06	-1,06	-0,37	-0,37	0,32	0,32	1,0	1,0		1,69		1,69		1371,28
	Pi	0,0405		0,1045		0,2103		0,2687		0,2181			0,1124				0.0455
6	nPi	4,05		10,45		21,03		26,87		21,81			11,24				4,55
7	Частоты, mi	6		8		15		40		16			8				7
8
9	20,7
10	52,96
11	7,26

В таблице 2.11 приведены следующие данные:

• в первой строке рабочей таблицы приведены значения границ интервалов х_i;

• вторая строка таблицы содержит значения середин интервалов ;

• в третьей строке рассчитываются значения ;

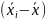• в четвертой строке рассчитываются значения ²;

• в пятой строке рассчитываются значения z= 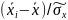, приняв

• х₁ = - , х_j = ;

• шестая строка содержит значения вероятностей попадания случайной величины в интервалы, рассчитанные с помощью функции НОРМСТРАСП: р_i - НОРМСТРАСП (z_i+1) НОРМ- СТРАСП (z_i);

• в седьмой строке приведены значения произведений пр_i;

• восьмая строка содержит значения эмпирических частот;

• девятая строка содержит значение ;

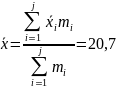• десятая строка содержит значение

• 

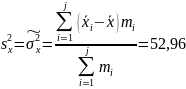
• одиннадцатая строка содержит значение ;

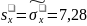2. Выбираем ячейку, в которую будет выведен результат вычислений ($А$14) и вызываем Мастер функций, нажав кнопку f_x - на панели инструментов. В Мастере функций из категории Статистические выбираем функцию ХИ2ТЕСТ 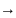ОК, появится окно функции ХИ2ТЕСТ.

Нажав кнопку в поле Фактический интервал и в таблице выделяем мышью строку 7 (В7:О7).

Нажав кнопку в поле Ожидаемый интервал, вводим данные выделяя мышью (В6:О6). В окне функции появится результат решения.

Нажмем кнопку ОК, в ячейке $А$14 появится результат вычислений α = Р(Y> ) = 0,036.

Вывод: Учитывая, что расчетное значение α = 0,036 α_кр = 0,05 то гипотеза о нормальности распределения выборки отвергается.
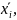
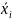