2.3. Проверка гипотезы о виде распределения по 𝜒2-критерию
Если закон распределения генеральной совокупности не известен, то по выборке проверяется гипотеза о виде закона распределения при помощи критериев согласия. Одним из наиболее используемых критериев является критерий 𝜒2-критерий.
Согласно этому критерию, наблюдаемое эмпирическое распределение выборки, выраженное абсолютными и относительными частотами сгруппированного ряда, сравнивается с гипотетическим теоретическим распределением соответствующей генеральной совокупности. Для этого выдвигается нулевая гипотеза Н0, утверждающая, что признак генеральной совокупности имеет функцию распределения F(x), которая сопоставляется с выборочной функцией и, в зависимости от величины отклонения эмпирического распределения от теоретического, выдвинутая гипотеза принимается или отвергается.
При проверке статистических гипотез о виде закона распределения строится интервальный (табл. 2.8) или дискретный вариационный ряд (табл. 2.7), где рi — вероятность попадания случайной величины в данный интервал для непрерывной случайной величины т.е. вероятность того, что случайная величина приняла данное значение для дискретной случайной величины, определяется согласно выдвинутой гипотезе, п — объем выборки.
Таблица 2.7. Дискретный вариационный ряд
Варианты, хi |
Х1 |
Х2 |
… |
хi |
… |
Xj |
Частоты, mi. |
m1 |
т2 |
… |
mi |
… |
mj. |
Вероятность, pi |
p1 |
p2 |
… |
pi |
… |
pj |
npi |
np1 |
пр2 |
… |
npi |
… |
npj |
Таблица 2.8. Интервальный вариационный ряд
Интервалы |
x1-x2 |
x2-x3 |
|
xi-1-xi |
xj-xj+1 |
Частоты, mi |
m1 |
т2 |
… |
mi |
… |
Вероятность, pi |
p1 |
p2 |
… |
pi |
… |
npi |
np1 |
пр2 |
… |
npi |
… |
По данным вариационного ряда определяется опытное значение критерия:
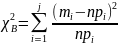
(2.4)
число степеней свободы k = j-r- 1,
где j — число вариант (интервалов) вариационного ряда, r — число оцениваемых параметров распределения.
Определяется
вероятность того, что случайная величина
Y
примет
значение больше
,
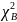т.е.
α = P(Y> ) = 1-F(y), (2.5)
где F(y) — функция распределения 𝜒2 которая определяется зависимостью:
.
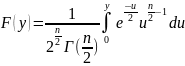По величине вероятности (2) принимается или отвергается выдвинутая гипотеза H0 о виде закона распределения случайной величины. Для принятия гипотезы используются стандартные вероятности αкр= 0,05; αкр = 0,10. При α > αкр гипотеза принимается, в противном случае гипотеза отвергается.
Пример 2.3. Задачи с дискретным вариационным рядом. Имеется нормально распределенная совокупность из 100 данных испытания ткани на гигроскопичность со средним значением 12% и стандартным отклонением 0,25. Сделайте случайную выборку 20 элементов из этой совокупности. Используя критерий 𝜒2 (хи-квадрат), проверьте, действительно ли выборка сделана из нормально распределенной генеральной совокупности.
В качестве точечных оценок математического ожидания и дисперсии примем соответствующие выборочные характеристики. Найдем их, используя инструменты пакета «Анализ данных».
Для этого в таблицу Excel в ячейки $А$2: $А$101 заносим данные генеральной совокупности, результаты испытаний. С помощью пакета Анализ данных и инструмента Выборка в ячейку В2 сделать выборку объемом 20 (табл. 2.9).
С помощью инструмента «Гистограмма» найдем опытные частоты m1.
В диалоговое окно входной интервал заносим исходные данные ячейки $А$2: $А$101, в интервал кармана заносим данные выборки $В$2: $В$21.
При использовании критерия ХИ-квадрат количество опытных значений в каждом интервале, т.е. частот, должно быть не менее пяти. Например, если в каком-то интервале их меньше, то интервалы объединяют, суммируя частоты, при этом значение берется как среднее арифметическое соответствующих им значений кармана.
С учетом данного условия перестроим таблицу частот вручную, и сформируем границы в ячейки Е2Е12, а соответствующие им опытные частоты mi в ячейки F2:F12.
Функция стандартного нормального распределения вычисляется с помощью встроенной статистической функции НОРМРАСП (х, среднее значение, стандартное отклонение, интегральный).
Таблица 2.9. Результаты вычислений
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
1 |
Результаты испы-таний, генсово-купнос-ти, ni
|
Выбор-ка |
|
|
Границы Интерва-ла |
Опыт-ные частоты mi |
НОРМ-РАСП |
Вероят-ности pi |
Расчет-ные частоты npi |
2 |
12,50 |
12,03 |
Кар-ман |
Часто-та |
|
|
|
|
|
3 |
12,63 |
11,9 |
11,29 |
4 |
11,3 |
8 |
0,00255 |
0,00255 |
0,2555 |
4 |
11,9 |
11,32 |
11,32 |
4 |
11,69 |
16 |
0,10748 |
0,10493 |
10,49326 |
5 |
11,65 |
12,4 |
11,32 |
0 |
11,9 |
6 |
0,34457 |
0,23709 |
23,70906 |
6 |
11,81 |
12,5 |
11,69 |
16 |
12,09 |
6 |
0,64057 |
0,29599 |
29,59982 |
7 |
11,41 |
12,5 |
11,8 |
2 |
12,28 |
8 |
0,86864 |
0,22806 |
22,80667 |
8 |
11,69 |
11,69 |
11,9 |
6 |
12,4 |
14 |
0,94520 |
0,07655 |
7,655759 |
9 |
11,32 |
12,68 |
11,9 |
0 |
12,5 |
12 |
0,97725 |
0,03204 |
3,204916 |
10 |
11,54 |
11,32 |
12,03 |
2 |
12,63 |
14 |
0,99413 |
0,01688 |
1,688239 |
11 |
11,29 |
11,9 |
12,03 |
0 |
12,64 |
10 |
0,99476 |
0,00063 |
0,063413 |
12 |
12,68 |
12,5 |
12,03 |
0 |
12,68 |
6 |
0,99673 |
0,00197 |
0,196951 |
13 |
12,56 |
11,8 |
12,28 |
8 |
итого |
100 |
|
|
|
14 |
12,32 |
12,03 |
12,4 |
14 |
|
|
|
хи2тест |
0,001 |
15 |
12,49 |
12,5 |
12,45 |
2 |
|
|
|
хи2обр |
2,16735 |
16 |
12,28 |
12,45 |
12,5 |
12 |
|
|
|
|
|
17 |
12,34 |
11,29 |
12,5 |
0 |
|
|
|
|
|
18 |
13,03 |
12,63 |
12,5 |
0 |
|
|
|
|
|
19 |
13,05 |
12,03 |
12,5 |
0 |
|
|
|
|
|
20 |
13,6 |
12,28 |
12,63 |
14 |
|
|
|
|
|
21 |
11,8 |
12,63 |
12,63 |
0 |
|
|
|
|
|
22 |
12,5 |
|
12,68 |
6 |
|
|
|
|
|
23 |
13,2 |
|
Еще |
10 |
|
|
|
|
|
24 |
12,4 |
|
итого |
100 |
|
|
|
|
|
25 |
12,56 |
|
|
|
|
|
|
|
|
26 |
12,6 |
|
|
|
|
|
|
|
|
… |
… |
|
|
|
|
|
|
|
|
Для этого выделить ячейку G3, и в диалоговое окно функции НОРМРАСП в поле Х вводим значения границ интервала, значение «интегральный» = 1 (истина), в поле «среднее значение» вводим 12 и «стандартное отклонение» 0,25 (из условий задачи). Если эти данные не заданы, то их можно получит с помощью инструмента «Описательная статистика» при этом входной интервал укажите $Е$3:$Е$12 и выходной $К$3.
В результате в ячейке G3 записывается формула (=НОРМ.РАСП(E3;12;0,25;1)) и значение нормального распределения. Потянуть за крестик до ячейки G12.
Вероятность pi - вычисляется как разность между значениями НОРМРАСП в последующей и предыдущей строках. Для этого в ячейку Н3 первое значение переносим без изменения, а далее результат вычисления.
Расчетные частоты npi вычисляем (в ячейки I3:I12) через вероятность попадания нормально распределенной величины в соответствующий интервал. Для этого значение вероятности умножаем на объем совокупности п. В нашем случае п=100.
Для вычисления статистики ХИ-квадрат в Excel встроена статистическая функция ХИ2ТЕСТ. В ячейку, например, Н14 записываем ХИ2ТЕСТ, в ячейке I14 ставим знак «=» и выбираем функцию ХИ2ТЕСТ, в открывшемся диалоговом окне в качестве «фактического интервала» вводятся опытные частоты (F3:F12), в качестве «ожидаемого» - расчетные частоты (I3:I12).
Граница критической области - квантиль распределения ХИ-квадрат может быть найдена с помощью встроенной статистической функции ХИ20БР. Аргумент «вероятность» - это уровень значимости (α = 0,05), а степени свободы k=j-r-1определяются как количество интервалов (в нашем случае k=10) за вычетом количества оцениваемых параметров (здесь - два: т и σ) минус единица, т.е.
k=10-2-1 =7
Гипотеза о нормальности распределения принимается, если выборочное значение статистики ХИ2ТЕСТ окажется меньше критического ХИ20БР.
Вывод. Учитывая, что выборочное значение статистики ХИ2ТЕСТ меньше критического ХИ20БР, т.е. 0,001 2,16735, то гипотеза о нормальности распределения выборки принимается.