2.2. Проверка гипотезы о равенстве средних. Двухвыборочный z-tect для средних

Пусть генеральные совокупности X и Y распределены нормально, причем их дисперсии известны (из предшествующего опыта или найдены теоретически). По независимым выборкам объемов п₁ и п₂ извлеченным из этих совокупностей, определены статистические оценки математического ожидания 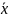и .

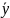Требуется по этим оценкам, при заданном уровне значимости α, проверить нулевую гипотезу, состоящую в том, что математические ожидания рассматриваемых совокупностей равны между собой.

Если окажется, что нулевая гипотеза справедлива, то различие статистических оценок математических ожиданий (выборочных средних) незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки.

Например, если физические величины А и В имеют одинаковые истинные размеры, а выборочные средние и . результатов измерений этих величин различны, то это различие незначимое.

Если нулевая гипотеза будет отвергнута, то различие выборочных средних значимо и не может быть объяснено случайными причинами, а объясняется тем, что сами генеральные средние различны.

В качестве критерия проверки нулевой гипотезы принимают случайную величину, имеющую нормальное распределение

Критическая область строится в зависимости от вида конкурирующей гипотезы, при этом рассматриваются три случая.

1. Нулевая гипотеза Н₀: М[Х] = М[Y].

Конкурирующая гипотеза H₁: М[Х] М[Y].

В этом случае строят двустороннюю критическую область исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости α.

Вычисляется наблюдаемое значение критерия 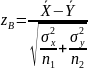(2.2):

(2.2)

Вычисляется значение функции Лапласа в критической точке:

Ф(z_кр) = 1-α

По значению функции Лапласа (см. приложение 2) определяют критическую точку z_кp.

Если |Z_B| < z_кp нет оснований отвергнуть нулевую гипотезу.

Если |Z_B| > z_кp, нулевую гипотезу отвергают.

2. Нулевая гипотеза H₀: М[Х] = M[Y].

Конкурирующая гипотеза H₁: М[Х] > М[Y].

На практике такой случай имеет место, если практические соображения позволяют предположить, что генеральная средняя одной совокупности больше генеральной средней другой совокупности. Например, если введено усовершенствование технологического процесса, то естественно допустить, что оно приведет к увеличению выпуска продукции.

В этом случае строят правостороннюю критическую область.

Вычисляются наблюдаемое значение критерия по формуле (2.3) и значение функции Лапласа в критической точке:

Ф(z_кр) = 1-α₂ (2.3)

По значению функции Лапласа определяют критическую точку z_кp.

Если z_B < z_кр, нет оснований отвергнуть нулевую гипотезу.

Если z_B > z_кр, нулевую гипотезу отвергают.

3. Нулевая гипотеза H₀: М[X] = M[Y].

Конкурирующая гипотеза H₁: М[Х] < М[Y].

В этом случае строят левостороннюю критическую область. Приняв во внимание, что критерий Z распределен симметрично относительно нуля, для нахождения критической точки необходимо ее определить, как во втором случае, а затем взять найденное значение со знаком «минус».

Если z_B > -Z_Kp, нет оснований отвергнуть нулевую гипотезу.

Если z_B < -z_кр, нулевую гипотезу отвергают.

Пример 2.2. Имеются две независимые выборки изделий из генеральных совокупностей X и Y, (табл. 2.4) генеральные дисперсии известны: 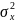= 25,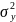0, = 4,0.

Таблица 2.4. Результаты замеров

Пресс 1 -Х	6,63	6,64	4,56	9,73	11,56	14,99	14,77	6,33	4,61	5,73
Пресс 2 -У	5,05	5,84	5,74	6,44	7,09	9.82	9.11	7,5	2.89	6,55

При уровне значимости α=0,01 проверить нулевую гипотезу Н₀:

М[Х] = М[Y] о равенстве генеральных математических ожиданий при конкурирующей гипотезе H₁: М[Х] М[Y].

Решение.

Рассчитываем средние значения выборок:

Вычисляем наблюдаемое значение критерия и значение

= 1,15

функции Лапласа в критической точке Ф(z_кр) = 1 - α= 0,99.

По значению функции Лапласа по таблице критических точек (см. приложение 2) определяем критическую точку z_кр = 2,58.

Так как z_B < z_Kp, нет оснований отвергнуть нулевую гипотезу, т.е. генеральные средние различаются незначимо.

Вероятность значимости для статистики z_B определяется следующим образом:

• рассчитывается величина Ө = arctg

• вероятность значимости находится с помощью интерполяции с использованием специальных таблиц Сукхатма (см. Fisher and Yates, 1974), где приведены 1%-е и 5%-е значения z для п₁ и п₂ равных 6, 8, 12, 24 и 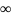, а также для Ө, равного 0°, 15°, 45°, 60°, 75°, и 90°.

Для z=1.15, Ө = arctg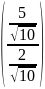 =68,3^о

с помощью линейной интерполяции находим P(Z z) = 0,25.

В пакете Анализ данных инструмент Двухвыборочный Z-тест для средних используется для проверки гипотезы о различии между средними двух генеральных совокупностей.

В категории Входные данные необходимо указать, кроме Интервалов переменной 1 и 2, Гипотетическую среднюю разность ∆ (для данного теста Excel использует вместо формулы (2.3) зависимость

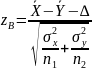значения Дисперсий переменной 1 (известной) и 2 (известной), а также значение Альфа — уровень значимости α.

Рассмотрим работу пакета анализа для проверки гипотезы о различии между средними.

Алгоритм действий следующий.

Формируем таблицу исходных данных:

	А	В	С	D	Е	F	G	Н	1	J	K
1	Пресс 1 -Х	6,63	6,64	4,56	9,73	11,56	14,99	14,77	6,33	4,61	5,73
2	Пресс 2 -У	5,05	5,84	5,74	6,44	7,09	9.82	9.11	7,5	2.89	6,55

Сервис /Анализ данных / Двухвыборочный Z-тест для средних -/ОК.

• Интервал переменной 1: $А$ 1 :$К$ 1.

• Интервал переменной 2: $А$2:$К$2.

• Гипотетическая средняя разность: 0 (значение по умолчанию).

• Дисперсия переменной 1 (известная): 25,0.

• Дисперсия переменной 2 (известная): 4,0.

• Альфа: 0,01.

• Выходной интервал: $А$6. ОК.

Excel представит результаты решения в следующем виде (рис. 2.3).

Двухвыборочный z-тест для средних
	Х	У
Среднее	8,555	6,603
Известная дисперсия и	25	4
Наблюдения	10	10
Гипотетическая разность средних (∆)	0
ZВ	1,146254
P(Z<=z) одностороннее (односторонняя вероятность значимости )	0,125845
z критическое одностороннее	1,644854
P(Z<=z) двухстороннее (двухсторонняя вероятность значимости)	0,25169
z критическое двухстороннее	1,959964

Рис. 2.3. Результаты решения задачи с помощью инструмента Двухвыборочный Z-тест для средних

Вывод: Так как z_B < z_Kp, нет оснований отвергнуть нулевую гипотезу, т.е. генеральные средние различаются незначимо. Следовательно, оба пресса выпускают продукцию отвечающую требованиям.