Контрольные вопросы

1. Чем вызвана необходимость применения статистических методов в управление процессом производства?

2. Сфера применения стандарта ГОСТ Р ИСО 10017-2005. Какие основные группы методов рекомендуются стандартом ГОСТ Р ИСО 10017-2005?

3. Назовите получаемые преимущества, ограничения и особенности и применение методов: описательной статистики, планирования экспериментов, моделирования и карт статистического управления процессом по ГОСТ Р ИСО 10017-2005?

4. Назовите получаемые преимущества, ограничения и особенности и применение методов: проверки гипотез, измерительного анализа, выборочного контроля и статистического назначения допусков по ГОСТ Р ИСО 10017-2005?

5. Назовите получаемые преимущества, ограничения и особенности и применение методов: регрессионного анализа, анализа возможностей процесса, анализа надежности и анализа временных рядов по ГОСТ Р ИСО 10017-2005?

6. В каких разделах стандартов ISO серии 9000 имеется ссылка на применение статистических методов?

7. Перечислите статистические методы, полезные для поддержки требований стандарта ИСО 9001.

8. От чего зависит выбор метода и способ его применения?

9. Назовите термины и определения в области статистического приемочного контроля по ГОСТ Р 50779.30-2000?

10. Назовите термины и определения в области статистического управления качеством по ГОСТ Р 50779.11-2000?

11. Назовите основные положения ГОСТ 24297-87(2001)?

12. Как осуществляется входной контроль продукции по ГОСТ 24297-87(2001)?

13. В чем сущность процедуры выборочного контроля по альтернативному признаку в соответствии с ГОСТ Р ИСО 2859-10-2008?

14. Назовите термины и определения ГОСТ Р 50779.10-2000 Статистические методы. Вероятность и основы статистики?

15. Назовите термины и определения ГОСТ Р 50779.52-95 Статистический приемочный контроль по альтернативному признаку.

16. Какие планы контроля предусмотрены стандартом ГОСТ Р 50779.52-95 Статистический приемочный контроль по альтернативному признаку?

17. Назовите термины, определения и применение ГОСТ Р 50779.70-99 Статистические методы. Процедуры выборочного контроля по альтернативному признаку?

18. Назовите термины, определения и применение ГОСТ Р 50779.50-95 Статистические методы. Приемочный контроль качества по количественному признаку?

19. Какие планы контроля предусмотрены стандартом ГОСТ Р 50779.50-95 Приемочный контроль качества по количественному признаку?

Практическая работа №2 проверка статистических гипотез

2.1. Проверка гипотезы о равенстве дисперсий - двухвыборочный f-tect для дисперсий

На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, самих методов измерений и т.д. Очевидно, предпочтительнее тот прибор, инструмент и метод, который обеспечивает наименьшее рассеивание результатов измерений, т.е. наименьшую дисперсию.

Проверяемая гипотеза называется нулевой и обозначается Н₀. Альтернативная гипотеза Н₁ - эта гипотеза, противоречащая нулевой.

Пусть генеральные совокупности Х и У распределены нормально. По независимым выборкам объемов п₁, и п₂, извлеченным из этих совокупностей, определены несмещенные статистические оценки дисперси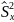й и :

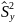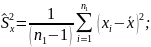
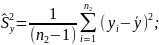
Требуется по этим дисперсиям при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой.

Если окажется, что нулевая гипотеза справедлива, т.е. генеральные дисперсии одинаковы, то различие вычисленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие вычисленных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность.

Если нулевая гипотеза будет отвергнута, т.е. генеральные дисперсии не одинаковы, то различие вычисленных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны. Например, если различие вычисленных дисперсий результатов измерений, произведенных двумя приборами, оказалось значимым, то точность приборов различна.

Критическая область строится в зависимости от вида конкурирующей гипотезы, при этом рассматривают два случая.

1. Нулевая гипотеза H₀: D[X] = D[Y].

Конкурирующая гипотеза H₁: D[X] > D[ У].

Вычисляется наблюдаемое значение критерия (отношение большей дисперсии к меньшей) (2.1):

F_B= 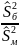(2.1)

По таблице критических точек распределения Фишера (см. приложения 1) по заданному уровню значимости α и числам степеней свободы f₁=n₁-1, f₂ =n₂-1 (f₁ — число степеней свободы большей дисперсии) определяют критическую точку F_kp (α, f₁, f₂).

Если F_B< F_кр, нет оснований отвергнуть нулевую гипотезу.

Если F_B > F_кр, нулевую гипотезу отвергают.

2 Нулевая гипотеза Н₀: D[X] = D[Y].

Конкурирующая гипотеза Н₁: D[X] 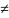D[Y].

Вычисляется наблюдаемое значение критерия по формуле (2.1).

Критическую точку F_КР (α/2, f₁, f₂) определяют по уровню значимости α/2, так как критическая область двусторонняя.

Если F_B < F_кр, нет оснований отвергнуть нулевую гипотезу.

Если F_B> F_кр, нулевую гипотезу отвергают.

Для измерения значимости рассматриваемого критерия (например, F_B) при отклонении нулевой гипотезы Н₀ используется односторонняя вероятность значимости P(F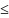 f), которая определяет вероятность принадлежности критерия множеству области принятия гипотезы в предположении, что верна нулевая гипотеза H₀. В этом случае выборка согласуется с нулевой гипотезой H₀, когда вероятность значимости в определенном смысле велика, и не согласуется, когда эта вероятность мала.

Чем меньше значение односторонней вероятности значимости P(F f), тем сильнее это свидетельствует против гипотезы H₀. С помощью вероятности значимости измеряют так называемую степень недоверия к основной гипотезе H₀. Она представляет собой дополнительную к вероятности значимости величину:

S_H=1-P(F f).

Близкая к нулю вероятность значимости интерпретируется как близость степени недоверия к единице, т.е. как очень сильный довод против гипотезы H₀. Близкая же к единице вероятность значимости показывает, что степень недоверия близка к нулю, т.е. доводы против H₀ слабы, что фактически указывает на согласие выборки с гипотезой H₀.

Вероятность значимости для первого случая проверки гипотезы определяется как:

P[F(n₁-l, n₂ -1) ],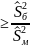

для второго случая: 2Р[F(n₁-l, n₂ -1) ], с использованием таблиц критических точек распределения Фишера.

Пример 2.1. Имеются две независимые выборки измерений точности размеров деталей обуви, полученных на двух прессах Х и У (табл. 1):

Таблица 1. Результаты замеров

Пресс 1- X	6,63	6,64	4,56	9,73	11,56	14,99	14,77	6,33	4,61	5,73
Пресс 2 - У	5,05	5,84	5,74	6,44	7,09	9,82	9,11	7,50	2,89	6,55

При уровне значимости α = 0,1 проверить нулевую гипотезу H₀:

D[X]=D[У] о равенстве генеральных дисперсий при конкурирующей гипотезе H₁: D[X] D[Y].

Решение.

Рассчитываем средние значения выборок:

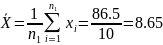
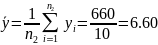
Рассчитываем статистические оценки дисперсий:

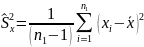=1/9 ∙[(6,63-8,65)²+ (6,64-8,65)²+(4,56-8,65)²+(9,73-8,65)²+(11,56-8,65)²+(14,99-8,65)²+(14,77-8,65)²+(6,33-8,65)²+(4,61-8,65)²+(5,73-8,65)²=15,81

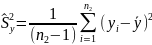=1/9 ∙[(5,05-6,60)²+(5,84-6,60)²+(5,74-6,60)²+(6,44-6,60)²+(7,09-6,60)²+(9,82-6,60)²+(9,11-6,60)²+(7,50-6,60)²+(2,89-6,60)²+(6,55-6,60)²=3,92

Вычисляем наблюдаемое значение критерия

F_B= =15,81/3,92=4,03

По таблице критических точек распределения Фишера (см. приложение 1) по заданному уровню значимости α = 0,05 и числам степеней свободы f₁ = п₁ - 1 = 9 и f₂ = п₂ - 1 = 9 определяем критическую точку F = 3,18. Так как F_B > F_Kp, нулевую гипотезу о равенстве генеральных дисперсий отвергаем.

Вероятность значимости определяется по таблице критических точек распределения Фишера P[F(9,9) 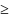4,04] = 0,025, при этом используем следующие данные таблицы:

		п1 = 9
п2=9	α = 0,05		3,18
	α = 0,01		5,35

В пакете «Анализ данных» инструмент «Двухвыборочный F-тест для дисперсий» применяется для сравнения дисперсий двух генеральных совокупностей (рис. 2.1).

Рис. 2.1. Окно Двухвыборочный F-тест для дисперсий

Алгоритм действий в Excel:

1. Формируем таблицу исходных данных:

	А	В	С	D	Е	F	G	Н	1	J	K
1	Пресс 1 -Х	6,63	6,64	4,56	9,73	11,56	14,99	14,77	6,33	4,61	5,73
2	Пресс 2 -У	5,05	5,84	5,74	6,44	7,09	9.82	9.11	7,5	2.89	6,55

2. Открыть Сервис / Анализ данных / Двухвыборочный F-тест для дисперсий / ОК.

3. Интервал переменной 1: $А$1:$К$1.

4. Интервал переменной 2: $А$2:$К$2.

5. Альфа: 0,05.

6. Выходной интервал: $А$6. И ОК.

Excel представит результаты решения в следующем виде (рис. 2.2).

Двухвыборочный F-тест для дисперсии
	Х	У
Среднее	8,555	6,603
Дисперсия	15,80814	3,91449
Наблюдения	10	10
df= п1 - 1	9	9
F	4,038365
P(F<=f) одностороннее	0,024765
F критическое одностороннее	3,178893

Рис. 2.2. Результаты решения задачи с помощью инструмента Двухвыборочный F-тест для дисперсий

Так как F > F_Kp, нулевую гипотезу о равенстве генеральных дисперсий отвергаем. Так как нулевая гипотеза отвергнута, и генеральные дисперсии не одинаковы, то различие вычисленных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны. Следовательно, качество деталей на 1 и 2 прессах различно.

При использовании данного Двухвыборочный F-тест для дисперсий рассчитывается только односторонний критерий, т.е. соответствующий первому случаю проверки гипотезы. Когда необходимо использовать двусторонний критерий, надо уровень значимости α уменьшить в два раза и использовать полученное значение для двустороннего критерия.