4.2. Корреляционный анализ
Диаграмма разброса показывает взаимосвязь между двумя видами данных и подтверждает их зависимость: это могут быть характеристика качества и влияющий на неё фактор, две различных характеристики качества, два фактора, влияющих на одну характеристику качества и т. д.
Для построения диаграммы рассеяния нужно не менее 30 пар данных (x,y). Оси x и y строят так, чтобы длины рабочих частей были примерно одинаковы. На диаграмму наносят точки (x,y), название диаграммы, а также интервал времени, число пар данных, названия осей, ФИО, должность исполнителя. Точки, далеко отстоящие от основной группы, являются выбросами, и их исключают (рис. 4.2).
Рис. 4.2. Диаграммы рассеяния: а) положительная корреляция, б) отрицательная корреляция, в) корреляция отсутствует, г) выбросы измерений из поля корреляции
Возможны различные варианты скоплений точек. Для установления силы связи полезно вычислить коэффициент корреляции r по формуле
где n – число пар данных;
xi, yi - собранные статистические данные;
, - средние арифметические значения x и y;
r – коэффициент корреляции (Множественный R ).
Коэффициент корреляции используют только при линейной связи между величинами. Значение r находится в пределах от –1 до +1. Считается, что при |r| < 0,2 линейная связь между переменными практически отсутствует, при 0,2 < |r| < 0,5 связь слабая, при 0,5 < |r| < 0,75 – средняя, при 0,75 < |r| < 0,95 – сильная. При |r| > 0,95 практически имеет место функциональная связь.
Можно оценить вероятность коэффициента корреляции mr. Для этого вычисляют его среднюю ошибку по формуле
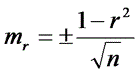
При r/mr > 3 коэффициент корреляции считается достоверным, то есть связь доказана. При r/mr <3 связь недостоверна, то есть, не доказана, а коэффициент корреляции незначим.
Также для проверки значимости полученных результатов необходимо найти критическое значение и вычислить значение статистики t, имеющей распределение Стьюдента с числом степеней свободы (n – 2).
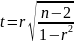
Пример 4.2. По экспериментальным данным (табл. 4.7), которые показывают: y, даН - разрывное усилие и x, см - толщину ткани. Необходимо оценить уровень связи между этими показателями качества ткани, построить диаграмму рассеяния, рассчитать коэффициент корреляции оценить достоверность коэффициента корреляции.
В пакете Анализ данных инструмент Корреляция используется для количественной оценки взаимосвязи между двумя диапазонами данных, представленных в безразмерном виде. Коэффициент корреляции выборки представляет собой ковариацию двух наборов данных, деленную на произведение их стандартных отклонений.
Таблица 4.7. Экспериментальные данные
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
0,20 |
0,19 |
0,28 |
0,26 |
0,23 |
0,21 |
0,24 |
0,26 |
0,28 |
0,25 |
Y |
64 |
65 |
69 |
69 |
66 |
65 |
67 |
67 |
70 |
68 |
№ |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
X |
0.25 |
0.22 |
0.18 |
0.26 |
0.17 |
0.30 |
0.19 |
0.25 |
0.29 |
0.27 |
Y |
67 |
66 |
63 |
68 |
62 |
70 |
64 |
68 |
69 |
68 |
№ |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
X |
0,20 |
0,19 |
0,29 |
0,31 |
0,24 |
0,22 |
0,27 |
0,23 |
0,25 |
0,17 |
Y |
63 |
66 |
70 |
72 |
66 |
65 |
69 |
65 |
69 |
61 |
Алгоритм действий следующий:
Формируем таблицу исходных данных в программе Excel.
В ячейки А1 внести Х и В1- У.
В ячейки А2:А31 располагаем значения Х.
В ячейки В2:В31- значения У.
Следующим шагом является построение диаграммы рассеяния, для этого необходимо выделить две строки значений х и у, далее выбрать на панели инструментов «Мастер диаграмм», выбрать тип диаграммы – «Точечная → Далее».
В следующем диалоговом окне – «Далее», в открывшемся окне заполняем поля заголовков (рис. 4.3), «отменить легенду → Далее → Готово». Диаграмма рассеяния готова.
Рис. 4.3. Диалоговое окно инструмента «Мастер диаграмм»
Для расчета выборочного коэффициента корреляции воспользуемся статистической функцией КОРРЕЛ. В ячейку, например А9, запишем коэффициент корреляции, а в ячейке В9 ставим знак «=» и в окне функции выбираем КОРРЕЛ (рис. 4.4).
Рис. 4.4. Диалоговое окно функции КОРРЕЛ
В открывшемся диалоговом окне заполняем поля: в «Массив 1» заносим значения Х, в «Массив 2» – значения У, затем ОК. Получаем коэффициент корреляции, равный 0,6834. Значение данного коэффициента свидетельствует о сильной связи между данными х и у , т.к. коэффициент корреляции r ≈0,7.
Коэффициент корреляции можно определить используя пакет Данные / Анализ / Анализ данных / Корреляция / ОК.
Входной интервал: $А$1: $В$31 (или выделить диапазон данных ХУ).
Поставить галочку: метка в первой строке.
Выходной интервал: $D$1.
Нажать кнопку ОК.
Excel представит результаты решения в виде (табл. 4.8).
Таблица 4.8. Данные связи двух переменных Х и У
(данные Корреляции)
|
Столбец Х |
Столбец У |
Столбец Х |
1 |
|
Столбец У |
0,683269863 |
1 |
Полученные результаты свидетельствуют о сильной связи между данными х и у , т.к. коэффициент корреляции r ≈0,7.
Далее требуется на заданном уровне значимости α=0,05 проверить нулевую гипотезу о равенстве нулю коэффициента корреляции для генеральной совокупности Н0: r = 0. Если нулевая гипотеза будет отвергнута, имеет место корреляция между х и у. Если же нулевая гипотеза принимается, то корреляция незначима: х и у некоррелированы (несмотря на то, что выборочный коэффициент корреляции r ≠ 0).
По условию нашей задачи нулевая гипотеза Н0: r = 0, альтернативная Н1: r > 0, следовательно, критическая область будет находиться в правом хвосте. Для проверки значимости вычисляем значение статистики t и находим критическое значение.
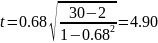
По условию задачи задан односторонний (правосторонний) критерий, выборочное значение статистики попало в критическую область, следовательно, нулевая гипотеза отвергается и наличие связи между Х и У подтверждается.
Далее определяем достоверность коэффициента корреляции: mr =(1-0,682)/301/2=0,098, а r/mr=0,68/0,098=6,94 > 3, следовательно, коэффициент корреляции является достоверным.