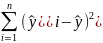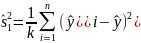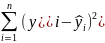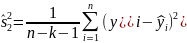- •Содержание
- •Введение
- •Практическая работа №1 статистические методы управления качеством в международных и российских стандартах
- •Контрольные вопросы
- •Практическая работа №2 проверка статистических гипотез
- •2.1. Проверка гипотезы о равенстве дисперсий - двухвыборочный f-tect для дисперсий
- •Самостоятельная работа по теме 2.1
- •2.2. Проверка гипотезы о равенстве средних. Двухвыборочный z-tect для средних
- •Самостоятельная работа по теме 2.2
- •2.3. Проверка гипотезы о виде распределения по 𝜒2-критерию
- •Самостоятельная работа по теме 2.3
- •Пример 2.4. Задачи с интервальным вариационным рядом.
- •Самостоятельная работа по теме 2.3
- •Практическая работа №3 факторный анализ. Дисперсионный анализ
- •3.1. Однофакторный дисперсионный анализ
- •Самостоятельная работа по теме 3.1
- •3.2. Двухфакторный дисперсионный анализ
- •Самостоятельная работа по теме 3.2
- •Практическая работа №4 корреляционный и регрессионный анализ
- •4.1. Регрессионный анализ
- •Самостоятельная работа по теме 4.1
- •4.2. Корреляционный анализ
- •Самостоятельная работа по теме 4.2
- •Список литературы
- •Значения критерия фишера (f-критерия)
- •115035, Москва, ул. Садовническая, 33, стр. 1
Самостоятельная работа по теме 3.2
Задание 3.3. В текстильном производстве выработана ткань на трех ткацких станках из пряжи двух поставщиков. Требуется выяснить, значимо ли влияние качества пряжи и настройки ткацких станков на качество готовой ткани, если разрывная нагрузка тканей составила (табл. 3.12). Сделайте выводы по результатам дисперсионного анализа.
Таблица 3.12. Разрывная нагрузка тканей
|
В1 |
В2 |
В3 |
А1 |
91 |
98 |
103 |
А2 |
85 |
96 |
105 |
Задание 3.4. В швейном цеху по производству верхней одежды имеется по два пресса для дублирования деталей одежды клеевым прокладочным материалом, который поступает от трех разных поставщиков. Требуется выяснить, значимо ли влияние настройки прессов и качества прокладочных материалов на качество готовой одежды, если прочность при расслаивании клеевого соединения дублированных деталей составила (табл. 3.13). Сделайте выводы по результатам дисперсионного анализа.
Таблица 3.13. Прочность при расслаивании клеевого соединения
|
В1 |
В2 |
В3 |
А1 |
7,5 |
9,3 |
10,1 |
А2 |
7,9 |
8,9 |
9,4 |
Сделайте выводы по результатам дисперсионного анализа.
Практическая работа №4 корреляционный и регрессионный анализ
4.1. Регрессионный анализ
При построении уравнения регрессии сначала необходимо установить наличие статистически значимых связей между переменными и оценить степень их тесноты. Виды корреляционных связей между измеренными признаками могут быть линейными и нелинейными, положительными или отрицательными. Возможна также ситуация, когда между переменными невозможно установить какую- либо зависимость. В этом случае говорят об отсутствии корреляционной связи. С целью выявления характеристик корреляционных зависимостей применяют корреляционный анализ. В задачи корреляционного анализа входит:
установление направления (положительное или отрицательное) и формы (линейная или нелинейная) связи между варьирующими признаками,
измерение тесноты связи (значения коэффициентов корреляции),
проверка уровня значимости коэффициентов корреляции.
Затем с использованием регрессионного анализа переходят к математическому описанию данного вида зависимостей. С этой целью определяют вид функций, связывающий результативный показатель у и аргументы х1, х2,..., хк, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных коэффициентов уравнения регрессии и анализируют точность полученной математической модели.
Уравнением регрессии называется функция, описывающая зависимость среднего значения результативного признака у от заданных значений аргументов х, т.е.
у = f(х1, х2,..., хк,, β0, β1,..., βk.).
Зависимость результативного показателя (отклика системы) у от аргументов (факторов) х1, х2,..., хк описывается полиномом вида:
y=
bo
+b1x1
+b2x2+b3x3+…+
bixi
+ b11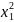 +
b22
+
b22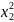 +
b33
+
b33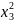 +
bij
+
bij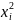 +…+ +
b12x1х2
+
b12x1х2+
b13x1х3+
b23x2х3+
b123x1х2
х3
+…+ bijxiхj
+…
+…+ +
b12x1х2
+
b12x1х2+
b13x1х3+
b23x2х3+
b123x1х2
х3
+…+ bijxiхj
+…
Данный полином называют регрессионной зависимостью (оценкой уравнения регрессии), а коэффициенты bi bii, bij - статистическими оценками коэффициентов регрессии. При этом bi - линейные коэффициенты, bii— нелинейные коэффициенты, bij — коэффициенты, учитывающие взаимное влияние факторов.
Задача регрессионного анализа заключается в экспериментальном определении коэффициентов регрессии b путем наблюдения за характером изменения входных переменных (факторов) и выходной величины (результативного показателя).
Значимость коэффициентов регрессии проверяется с помощью t-критерия Стьюдента.
При проведении регрессионного анализа рассчитываются показатели так называемой регрессионной статистики:
множественный коэффициент корреляции
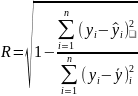 (4.1)
(4.1)
где
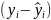 – регрессионные остатки;
– регрессионные остатки;
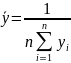 - среднее
результативного признака;
- среднее
результативного признака;
квадрат множественного коэффициента корреляции - коэффициент детерминации- R2;
нормированный коэффициент детерминации:
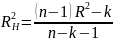 (4.2)
(4.2)
стандартную ошибку
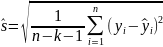 (4.3)
(4.3)
Для исходных данных проводится однофакторный дисперсионный анализ, при этом рассчитываются (табл. 4.1):
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Оценка дисперсии |
Межгрупповая |
|
k |
|
Остатки |
|
n-k-1 |
|
Полная (общая) |
|
п - 1 |
|
расчетное значение F-критерия FB = / ;
значимость F определяется так же, как при рассмотрении двухвыборочного F -теста о равенстве дисперсий (см. лаб работу №2/1);
Р – вероятность значимости определяется так же, как при рассмотрении парного двухвыборочного t-теста.
Расчетное значение FB сравнивается с FKp(α; к; п-к-1), определяемого по таблице критических точек распределения Фишера (см. приложения). При этом проверяется нулевая гипотеза Н0: β = 0.
Если FB > FKр, гипотеза Н0 отвергается, т.е. хотя бы один коэффициент регрессии bj. не равен нулю. В множественном регрессионном анализе исследуется зависимость величины у от нескольких независимых переменных х1, х2,..., хк.
Пример 4.1. На основе линейной регрессионной модели исследовать зависимость прочности ткани (у) от прочности нитей (х1), плотности ткани (х2) и количества аппрета (х3). Имеются данные 15 наблюдений (табл. 4.2)
Таблица 4.2
Номер опыта |
Y |
Х1 |
Х2 |
Х3 |
1 |
60 |
60 |
300 |
5 |
2 |
58 |
60 |
300 |
2 |
3 |
66 |
60 |
400 |
5 |
4 |
62 |
60 |
400 |
2 |
5 |
69 |
60 |
500 |
2 |
6 |
68 |
70 |
300 |
5 |
7 |
65 |
70 |
300 |
2 |
8 |
70 |
70 |
400 |
5 |
9 |
72 |
70 |
400 |
2 |
10 |
75 |
70 |
500 |
2 |
11 |
90 |
80 |
500 |
5 |
12 |
80 |
80 |
400 |
2 |
13 |
85 |
80 |
400 |
5 |
14 |
83 |
80 |
300 |
5 |
15 |
75 |
80 |
300 |
2 |
Решение.
В программе Excel в пакете Анализ данных инструмент Регрессия предлагает линейный регрессионный анализ, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.
Рассмотрим работу пакета для проведения регрессионного анализа.
В открывшееся окно в категории Входные данные необходимо указать:
Входной интервал у — диапазон анализируемых зависимых данных, диапазон должен состоять из одного столбца;
Входной интервал X — диапазон независимых данных, подлежащих анализу. Excel располагает независимые переменные этого диапазона слева направо в порядке возрастания. Максимальное число входных диапазонов равно 16;
Константа ноль — установите флажок, чтобы линия регрессии прошла через начало координат (коэффициент b0 = 0);
Уровень надежности — установите флажок, чтобы включить в выходной диапазон дополнительный уровень. В соответствующее поле введите уровень надежности, который будет использован дополнительно к уровню 95%, применяемому по умолчанию.
Excel предлагает в качестве параметров вывода Остатки (Остатки; Стандартизованные остатки; График остатков; График подбора) и Нормальную вероятность (График нормальной вероятности) - везде установить флажок.
Алгоритм действий следующий.
Формируем таблицу исходных данных (табл. 4.3):
Сервис / Анализ данных / Регрессия / ОК.
Входной интервал Y: $А$ 1: $А$ 16.
Входной интервал X: $В$1:$D$ 16.
Уровень надежности: 90 %.
Выходной интервал: $А$18.
Поставить флажки в категории Остатки и Нормальная вероятность.
ОК.
Excel представит результаты решения таблично в следующем виде (табл. 4.4).
Таблица 4.3
|
А |
В |
С |
D |
E |
1 |
Номер опыта |
Y |
Х1 |
Х2 |
Х3 |
2 |
1 |
60 |
60 |
300 |
5 |
3 |
2 |
58 |
60 |
300 |
2 |
4 |
3 |
66 |
60 |
400 |
5 |
5 |
4 |
62 |
60 |
400 |
2 |
6 |
5 |
69 |
60 |
500 |
2 |
7 |
6 |
68 |
70 |
300 |
5 |
8 |
7 |
65 |
70 |
300 |
2 |
9 |
8 |
70 |
70 |
400 |
5 |
10 |
9 |
72 |
70 |
400 |
2 |
11 |
10 |
75 |
70 |
500 |
2 |
12 |
11 |
90 |
80 |
500 |
5 |
13 |
12 |
80 |
80 |
400 |
2 |
14 |
13 |
85 |
80 |
400 |
5 |
15 |
14 |
83 |
80 |
300 |
5 |
16 |
15 |
75 |
80 |
300 |
2 |
Таблица 4.4
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|||||||||
Регрессионная статистика |
|
|
|
|
|
|||||||||||
Множественный R |
0,978659 |
|
|
|
|
|
|
|
||||||||
R-квадрат |
0,9577 |
|
|
|
|
|
|
|
||||||||
Нормированный R-квадрат |
0,9462 |
|
|
|
|
|
|
|
||||||||
Стандартная ошибка |
2,1902 |
|
|
|
|
|
|
|
||||||||
Наблюдения |
15 |
|
|
|
|
|
|
|
||||||||
|
||||||||||||||||
Дисперсионный анализ |
|
|
|
|
|
|
||||||||||
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
||||||||
Регрессия |
3 |
1196,963 |
398,987 |
83,16 |
7,64E-08 |
|
|
|
||||||||
Остаток |
11 |
52,77078 |
4,79734 |
|
|
|
|
|
||||||||
Итого |
14 |
1249,733 |
|
|
|
|
|
|
||||||||
|
||||||||||||||||
|
Коэффициенты |
Стандартная ошибка |
t-статис-тика |
P-значение |
Нижние 95% |
Верхние 95% |
Нижние 90,0% |
Верхние 90,0% |
||||||||
Y-пересечение |
17,462 |
5,721653 |
3,05191 |
0,011 |
-30,05 |
-4,86 |
-27,73 |
-7,186 |
||||||||
Х1 |
0,9464 |
0,070221 |
13,4787 |
0,034 |
0,791 |
1,101 |
0,820 |
1,072 |
||||||||
Х2 |
0,0507 |
0,007602 |
6,67273 |
0,035 |
0,034 |
0,067 |
0,037 |
0,064 |
||||||||
Х3 |
1,1171 |
0,385304 |
2,89940 |
0,014 |
0,269 |
1,965 |
0,425 |
1,809 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
ВЫВОД ОСТАТКА |
|
|
|
ВЫВОД ВЕРОЯТНОСТИ |
|
|||||||||||
Наблюдение |
Предсказанное Y |
Остатки |
Стандарт. остатки |
|
Персентиль |
Y |
|
|
||||||||
1 |
60,1310 |
-0,13108 |
-0,06751 |
|
3,3333 |
58 |
|
|
||||||||
2 |
56,7796 |
1,22038 |
0,628583 |
|
10 |
60 |
|
|
||||||||
3 |
65,2038 |
0,796198 |
0,410099 |
|
16,666 |
62 |
|
|
||||||||
4 |
61,8523 |
0,147657 |
0,076054 |
|
23,333 |
65 |
|
|
||||||||
5 |
66,9250 |
2,074934 |
1,068739 |
|
30 |
66 |
|
|
||||||||
6 |
69,5959 |
-1,59593 |
-0,82202 |
|
36,666 |
68 |
|
|
||||||||
7 |
66,2444 |
-1,24447 |
-0,64099 |
|
43,333 |
69 |
|
|
||||||||
8 |
74,6686 |
-4,66866 |
-2,40469 |
|
50 |
70 |
|
|
||||||||
9 |
71,3172 |
0,682803 |
0,351692 |
|
56,666 |
72 |
|
|
||||||||
10 |
76,3899 |
-1,38992 |
-0,71591 |
|
63,333 |
75 |
|
|
||||||||
11 |
89,2062 |
0,793767 |
0,408846 |
|
70 |
75 |
|
|
||||||||
12 |
80,7820 |
-0,78205 |
-0,40281 |
|
76,666 |
80 |
|
|
||||||||
13 |
84,1335 |
0,86649 |
0,446304 |
|
83,333 |
83 |
|
|
||||||||
14 |
79,0607 |
3,939213 |
2,028975 |
|
90 |
85 |
|
|
||||||||
15 |
75,7093 |
-0,70933 |
-0,36535 |
|
96,666 |
90 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
Регрессионная статистика в (табл. 4.4) представлена:
- множественный R - множественный коэффициент корреляции (формула 4.1);
- R-квадрат - квадрат множественного коэффициента корреляции - коэффициент детерминации;
- нормированный R-квадрат - нормированный квадрат множественного коэффициента корреляции (формула 4.2);
 стандартная
ошибка (формула
4.3);
стандартная
ошибка (формула
4.3);наблюдения - количество наблюдений.
Дисперсионный анализ в таблице 4.4 представлен для регрессии и остатков:
df — число степеней свободы;
SS— суммы квадратов разностей;
MS — оценки дисперсий;
F— вычисленное значение критерия Фишера (FB),
значимость F.
Данные для уравнения регрессии в таблице представлены:
для переменной xQ (Y— пересечение),
коэффициенты — bQ, b1, b2и b3;
стандартная ошибка (10.3) -
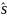 b0,
b1,
b2
и
b2;
b0,
b1,
b2
и
b2;t-статистика — tb0, tb1, tb2, и tb3.
P-значение — вероятность значимости;
нижние 95% и верхние 95%, нижние 90% и верхние 90% - интервальные оценки для коэффициентов регрессии с доверительной вероятностью р=0,95 и р=0,90 соответственно.
ВЫВОД ОСТАТКА в данной таблице представлены:
наблюдения - порядковый номер значения прочности ткани (у) в таблице исходных данных;
предсказанное у - значение производительности труда (
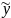 ),
рассчитанное
по уравнению регрессии;
),
рассчитанное
по уравнению регрессии;остатки -
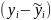 ;
;стандартные остатки.
ВЫВОД ВЕРОЯТНОСТИ в (табл. 4.4) представлены:
персентиль — рассчитывается для каждого значения у как сумма предшествующего вычисленного значения
персентиля и h=(100%/наблюдение);
начальное и конечное значения персентиля рассчитываются как (0 + h/2) и (100 - h/2) — соответственно;
у — значения производительности труда, расположенные в порядке возрастания.
Кроме таблиц Excel представит следующие графики.
График нормального распределения, построенный по данным таблицы ВЫВОД ВЕРОЯТНОСТИ (рис. 4.1).
Рис. 4.1. График нормального распределения
А также графики остатков для переменных х1 , х2 и х3 и графики подбора для переменных х1 , х2 и х3.
Таким образом, уравнение регрессии имеет вид:
У=17,462 + 0,946485Х1 + 0,050727Х2 + 1,117153Х3
Проверяем значимость коэффициентов уравнения регрессии по критерию Стьюдента. При нулевой гипотезе Но: β=0, если tВ tкр нулевая гипотеза отклоняется, и принимается гипотеза, что коэффициенты значимы.
Значение t-критерия
табличного при числе степеней свободы
f=15-3-1=11
и α=0,05, tкр=2,201.
Если
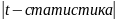 tкр,
то коэффициенты значимы. Учитывая, что
tb1=13,47871>tкр,
tb2=6,672734>
tкр
и tb3=2,899409>
tкр,
то коэффициенты уравнения регрессии
значимы.
tкр,
то коэффициенты значимы. Учитывая, что
tb1=13,47871>tкр,
tb2=6,672734>
tкр
и tb3=2,899409>
tкр,
то коэффициенты уравнения регрессии
значимы.
Учитывая, что расчетное значение критерия Фишера FB=83,168 больше табличного Fкр=7,64, то нулевая гипотеза, что β=0, отвергается, т.е. полученное уравнение регрессии значимо и
хотя бы один из коэффициентов уравнения не равен нулю.
Р-значение оценивает значимость математической модели. Регрессионная модель значима, если вероятность ошибки Р меньше заданного уровня значимости (по умолчанию 0,05). В нашем случае все р-значения для переменных х меньше 0,05. Значит модель значима.
Если окажется, что некоторые из факторов незначимы, то в этом случае надо строить новую модель, удалив незначимые факторы, воспользовавшись пошаговой регрессией.