Метрические задачи

Положение точки относительно плоскостей проекций. Точка принадлежит плоскости, если проекции точки лежат на соответствующих проекциях прямой, принадлежащих данной плоскости. Если точка лежит в плоскости проекций, то ее проекция на эту плоскость совпадает с самой точкой, а две другие проекции располагаются на осях проекций (рис. 21).

с

Две проекции точки, лежащие на оси проекций, совпадают с самой точкой, а третья находится в начале координат.

с

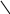
Рис. 21. Проекции точек, лежащих на плоскостях проекций

Нахождение натуральной величины треугольника способом перемены плоскостей. Введем две дополнительные плоскости проекций (рис. 22):

1. V₁ H и V₁ ABC.

2. H₁ V₁ и H₁ ABC.

l₁

l₂

l₃

n₁

n₂

n₃

Р ис. 22. Определение натуральной величины треугольника способом перемены плоскостей

1. Так как V₁ H и V₁ ABC, то ABC является проецирующим в плоскости V₁. Для построения проекции ABC в плоскости V₁ построим горизонталь (А1): ее фронтальная проекция (a’1’), горизонтальная проекция (a1).

2. Перпендикулярно горизонтальной проекции (a1) проведем ось X₁ — горизонтальный след плоскости V₁.

3. Проведем через точки a, b, c прямые l₁, l₂, l₃ (a1).

4. От оси X₁ на l₁, l₂, l₃ отложим отрезки z_A, z_B, z_C, которые должны лежать на одной прямой. Отрезок (c₁b₁) — фронтальная проекция ABC в плоскости V₁.

5. Рассмотрим плоскости H₁ V₁ и H₁ ABC, в ней ABC является треугольником уровня и виден в натуральную величину. Проведем ось X₂ (c₁b₁) — след плоскости H₁ в плоскости V₁.

6. Проведем через точки a₁, b₁, c₁ прямые n₁, n₂, n₃ X₂.

7. На прямых n₁, n₂, n₃ отложим от оси X₂ расстояния y_A, y_B, y_C и получим точки a₂, b₂, c₂.

8. a₂ b₂ c₂ является натуральной величиной ABC.

Нахождение натуральной величины треугольника способом вращения без указания на чертеже осей вращения, перпендикулярных плоскостям V и H. Порядок построения указан на рис. 23.

Рис. 23. Определение натуральной величины треугольника методом вращения

Поворот вокруг оси H, проходящей через точку a до положения ABC V

1. В ABC проводим горизонталь (А1): в a’b’c’ проведем прямую (a’1’) X.

2. В abc найдем проекцию горизонтали (a1).

3. На свободном поле чертежа проведем прямую (a₁1₁) V, или, что то же самое (a₁1₁) X.

4. От точки a₁ сделаем засечку радиусом r₁, от точки 1₁ сделаем засечку радиусом r₂ и на пересечении получим точку b₁.

5. Проведем прямую через точки b₁ и 1₁ и на ней от точки 1₁ радиусом r₃ получим точку c₁.

6. Из точек a’, b’, c’ проведем прямые параллельно оси X, из точек a₁, b₁, c₁ проведем перпендикуляры к оси X, на их пересечении получаем точки a₁’, b₁’, c₁’. Отрезок (b₁’ c₁’) — фронтальная проекция ABC.

Поворот вокруг оси V, проходящей через точку c₁ до положения ABC H

1. Через точку c₁’ проведем прямую l X.

2. Радиусами (c₁’a₁’), (c₁’b₁’) сделаем засечки на прямой l и получим точки a₂’, b₂’.

3. Из точек a₂’, b₂’, c₁’ проведем прямые перпендикулярно X, из точек a₁, b₁ проведем прямые параллельно X, на их пересечении получим точки a₂, b₂.

4. a₂ b₂ c₁ — натуральная величина ABC.