Раздел 2. Основы алгоритмизации. Программирование.

1. Основные понятия и определения

Алгоритмизация - это процесс построения алгоритма решения задачи, результатом которого является выделение этапов процесса обработки данных, формальная запись содержания этих этапов и определение порядка их выполнения.

Алгоритм - это точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату.

Свойства алгоритма:

1. детерминированность - точность указаний, исключающая их произвольное толкование;

2. дискретность - возможность расчленения вычислительного процесса на отдельные элементарные операции, возможность выполнения которых не вызывает сомнений;

3. результативность - прекращение процесса через определенное число шагов с выдачей искомых результатов или сообщения о невозможности продолжения вычислительного процесса;

4. массовость - пригодность алгоритма для решения всех задач заданного класса.

Алгоритмический язык - набор символов и правил образования и истолкования конструкций их этих символов для записи алгоритмов.

Язык программирования - предназначен для реализации программ на

ЭВМ.

Программа - это алгоритм, записанный в форме, воспринимаемой машиной. Программа содержит наряду с описанием данных команды, в какой последовательности, над какими данными и какие операции должна выполнять машина, а также в какой форме следует получить результат. Это обеспечивают различные операторы.

Данные - это факты и идеи, представленные в формализованном виде, позволяющем передавать или обрабатывать эти факты и идеи с помощью некоторого процесса.

Оператор - совокупность символов, указывающих операцию и значения, либо местонахождение ее элементов.

А:= В+С; {А, В, С - переменные}

К:=2;

IF T< 0 THEN . . .

Переменная - это объект, который в ходе выполнения программы может менять свое значение.

Свойства переменной:

1. переменная называется неопределенной до тех пор, пока она не получит значение:

а) вводом извне;

б) занесением константы;

в) занесением значения другой, уже ранее определенной переменной;

35

2. в каждый момент времени переменная может иметь определенное значение, либо быть неопределенной;

3. последующее значение уничтожает (стирает) предыдущее значение. Выбор (чтение) из переменной и ее использование не изменяют значения переменной.

Предметом курса являются методы и средства составления алгоритмов и программ с целью решения задач на ЭВМ.

Для разработки программ используются системы программирования.

Система программирования - средство автоматизации

программирования, включающее язык программирования, транслятор этого языка, документацию, а также средства подготовки и выполнения программ.

Транслятор - это программа, которая переводит с одного языка на другой.

Интерпретатор - это программа, которая сразу выполняет переводимые команды.

Компилятор - это программа, которая переводит конструкции алгоритмического языка в машинные коды.

2. Алгоритмизация линейных вычислительных процессов

Для записи линейных алгоритмов применяются следующие блоки (рис.1):

начало, f ^ ввод, вывод / 7 вычисления

конец ^{4 J} *- '

Рисунок 2.1 - Основные элементы схем линейных алгоритмов.

Этапы решения задачи на ЭВМ

Словесная постановка задачи. Этот этап предполагает точную формулировку задачи и цели, которые необходимо достигнуть при ее решении. Определение целей сводится к нахождению исходных и промежуточных величин, а также результатов, т.е.

дано:

определить:

промежуточные величины.

Математическая постановка задачи заключается в записи условия задачи в виде математических соотношений с использованием выше выбранных переменных. На этом же этапе осуществляется выбор математического метода решения задачи согласно составленной математической модели. Метод должен обеспечить решение задачи выполнением последовательности четырех арифметических операций и функций. Для простых задач обычно метод решения очевиден, и этот этап опускается.

Разработка алгоритма и его графическое описание. Алгоритмизация задачи представляет собой первый этап программирования. В процессе его выполнения устанавливается необходимая последовательность арифметических и логических действий, с помощью которых реализуется выбранный численный метод. Эту последовательность можно записать в виде схемы алгоритма.

36

Запись алгоритма на языке программирования. Алгоритм, записанный в графическом виде, далее записывается в виде последовательности операторов выбранного языка программирования, т.е. составляется программа решения задачи.

Разработка контрольного теста и отладка программы. Отладка программы необходима для выявления и устранения ошибок, допущенных на предыдущих этапах. Правильность выполнения программы осуществляется сравнением результатов, полученных при расчете нескольких вариантов задачи вручную и на ЭВМ. Полученный вручную расчет является контрольным тестом. Такой метод называется тестированием программы.

Работа на ЭВМ с получением результатов. После решения задачи на ЭВМ необходим анализ результатов. Решение задачи на ЭВМ производится по отлаженной программе для всего множества исходных данных. Анализ результатов выполняется, как правило, лицом, в интересах которого решалась задача.

Разработка алгоритмов линейных процессов

Пример 1

Словесная постановка задачи. Определить площадь и длину второго катета прямоугольного треугольника, если известны длина одного катета и длина гипотенузы.

Дано: а - длина катета,

с - длина гипотенузы.

Определить: b - длина искомого катета,

S - площадь треугольника.

Промежуточные величины: нет.

Математическая постановка. По теореме Пифагора имеем: с² = а² + b², откуда b = V с² — а ²

Тогда площадь

Разработка схемы алгоритма. В первую очередь необходимо вычислить b = V с² — а², затем s = а - Ь/2 .

Схема алгоритма будет иметь вид (рис.2):

вывод b,S

Рисунок 2.2 - Схема алгоритма Так как алгоритм состоит из последовательно выполняемых действий, то он описывает линейный процесс.

37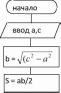

Пример 2

Словесная постановка. Определить длину ломаной линии, состоящей из трех звеньев, если известны координаты вершин (рис.2.3).

Дано: координаты вершин x1,y1,x2,y2,x3,y3,x4,y4.

Определить: L - длина ломаной.

Промежуточные величины: LI, L2, L3 - длины звеньев ломаной.

Рисунок 2.3

Математическая постановка. Для определения длин составляющих звеньев воспользуемся формулой для вычисления расстояния между двумя точками плоскости.

L1 = yl((x2 - x1)² + (y2 - y1)²) , L2 =yj((x3 - x2)² + (y3 - y2)²) ,

L3 =yj((x4 — x3)² + (y4 — y3)²) , откуда L = L1 + L2 + L3 .

Разработка схемы алгоритма.

Схема алгоритма будет иметь вид:

("начало '')

/ввод x1,y1,x2,y2, x4,y4

I

вычисл. L1

~ I

вычисл. L2

: I zz

вычисл. L3

I ZZ L=L1+L2+L3

I вывод L J

конец

Рисунок 2.4 - Схема алгоритма

Пример 3

Словесная постановка задачи. Тело брошено вертикально вверх с некоторой скоростью V. Определить время, за которое тело пролетит заданное расстояние S.

Дано: V - скорость; S - расстояние; g = 9,8 - ускорение свободного падения.

Определить: t - время.

Промежуточные величины: D.

Математическая постановка задачи. Расстояние рассчитывается по формуле, известной из физики:

S = Vt - —;

2

38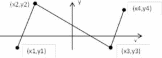

отсюда 2S = 2Vt - gt².

Так как нам нужно определить t, запишем это выражение в виде квадратного уравнения: gt² - 2Vt + 2S = 0.

Получена математическая модель задачи в виде квадратного уравнения.

Выбор численного метода решения задачи. Этот этап в предыдущих задачах отсутствовал, т.к. метод решения был очевиден (с использованием полученных расчетных формул). В этой задаче необходимо применить формулы решения квадратного уравнения.

В общем виде уравнение имеет вид:

ах + Ьх + с = 0.

Определим дискриминант и корни: D = b - 4ac ;

x1 = -ь + Ур ;

2a

x2 = ^-ь .

2a

Для данной задачи справедливы следующие соотношения: a = g; b = -2v; c = 2s; x = t.

Тогда: D = 4V² - 4g2s = 4V² - 8gS;

2. _ 2v+VD .

²g ;

^2 = 2v -Vd ²g

Разработка схемы алгоритма. Вычисляем последовательно D, t1, Схема алгоритма приведена на рисунке 2.5.

С начало ^

• J

t2.

ввод s,v,g

вывод t1,t2

г

Л

.конец j

Рисунок 2.5 - Схема алгоритма

3. Разветвляющиеся вычислительные процессы

1. Типы разветвляющихся алгоритмов

Второй типовой структурой алгоритмов является разветвляющийся вычислительный процесс, в котором направление вычислений зависит от результата проверки некоторого условия. Направления, по которым может

39

следовать вычислительный процесс, называются ветвями. В программах разветвляющихся процессов естественный порядок выполнения операторов нарушается и обеспечивается выполнение той последовательности операторов, которая соответствует выбранным условиям. В языке Паскаль это реализуется специальными управляющими операторами или операторными структурами, которые называются операторами перехода.

Схему алгоритма разветвленной структуры характеризует наличие блока "условие", который имеет два выхода, помеченные словами "да" и "нет". Еще этот блок называют логическим блоком. В этом блоке осуществляется проверка выполнения некоторого логического условия. Если условие "истинно", вычислительный процесс идет по выходу "да", в противном случае - по выходу "нет".

Различают три типа разветвляющихся алгоритмов, функциональные схемы которых приведены на рисунке 2.6.

выход

в

Рисунок 2.6 - Функциональные схемы разветвляющихся процессов

Ветвление, представленное на рис.6(а), называется обходом, так как оператор S, записанный в арифметическом блоке, не выполняется, если условие В ложно. При реализации вычислительного процесса арифметический блок будет обойден, и направление вычислений пойдет по ветви "нет".

Выбор из двух возможностей, или альтернатива, представлен на рис.6(б). Если проверяемое условие В будет истинным, выполнится оператор S1, в противном случае выполнится оператор S2. Отметим, что алгоритм обхода является частным случаем альтернативы.

Выбор из многих возможностей представлен на рис.6(в). Здесь В^ i=1,K представляют собой условия выбора, в зависимости от значений которых выполняется один из соответствующих им операторов S1, S2, . . , SK.

40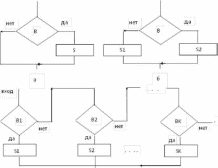

2. Операторы перехода.

Назначение операторов перехода состоит в организации безусловных и условных переходов в программе в зависимости от результата проверки логического условия В.

2. . Операторная запись обхода. Разветвление такого типа может быть записано с помощью условного оператора, который имеет вид на псевдоязыке:

ЕСЛИ < выражение > ТО < оператор > , где ЕСЛИ (IF) и ТО (THEN) - ключевые слова;

• выражение > - логическое условие;

• оператор > - оператор.

При решении практических задач бывает необходимо в зависимости от результата проверки, выполнить (или обойти) группу операторов. На алгоритмическом языке предоставляет возможность сделать из группы операторов один составной оператор, заключив группу операторов в операторные скобки НАЧАЛО и КОНЕЦ.

Тогда условный оператор для записи обхода группы операторов имеет

вид:

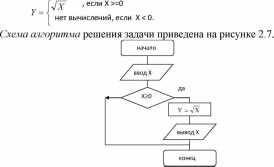
ЕСЛИ < выражение > ТО Начало < S1, S2, . . , SN > Конец;. Пример. Вычислить и вывести на экран корень квадратный из положительного числа Х, значение которого не превышает 1000. В случае отрицательного числа никаких вычислений в программе не производится. Дано: Х - исходное число.

Математическая запись задачи:

Рисунок 2.7

Программа на псевдоязыке.

Начало ВВОД( X );

ЕСЛИ X >= 0 ТО

• :=SQRT ( X );

ВЫВОД( ' Корень из Х равен ', Y : 6:2) Конец ЕСЛИ

41

Конец.

2. Операторная запись альтернативы. Выбор из двух возможностей реализуется условным оператором, имеющим следующий синтаксис:

ЕСЛИ <выражение> ТО <оператор 1> ИНАЧЕ <оператор 2>; где ИНАЧЕ (ELSE) - ключевое слово.

Если <выражение> истинно, то выполняется <оператор 1>, в противном случае - <оператор 2>.

Оператор, стоящий после ключевого слова ИНАЧЕ, может быть любым оператором, в том числе и условным. Кроме того, <оператор 1> и <оператор2> могут быть составными операторами.

Ниже приведена одна из возможных конструкций условного оператора:

ЕСЛИ B1 ТО Начало <S 1, S2> Конец

ИНАЧЕ ЕСЛИ B2 ТО <S3> ИНАЧЕ <S4>;

Здесь B1 и B2 - логические условия. <Оператор 1> представляет собой составной оператор, а <оператор 2> - условный оператор ЕСЛИ - ТО - ИНАЧЕ. Если логическое условие В1 истинно, выполнятся S1 и S2, и управление будет передано следующему в программе оператору. Если логическое условие В1 ложно, выбирается <оператор 2>. При его выполнении проверяется условие В2: в случае истинности выражения В2 выполняется оператор S3, в противном случае - S4.

Пример.

Словесная постановка задачи. Вычислить корни квадратного уравнения. Квадратное уравнение имеет вид:

aX² + bX + c = 0.

Словесное описание задачи:

1. Ввести значения коэффициентов квадратного уравнения a, b и с.

2. Вычислить значение D = b - 4ac.

3. Сравнить D с нулем. Если D < 0, перейти к п. 6.

4. Вычислить X1 = ( -b + Vd )/( 2a); X2 = ( -b -Vd )/( 2a ).

5. Вывести на печать значения X1 и X2. Перейти к п. 7.

6. Вывести сообщение об отсутствии действительных корней уравнения.

7. Прекратить вычисления.

Схема алгоритма решения задачи приведена на рисунке 2.8.

D = Ь²-4ас

Рисунок 2.8. Схема алгоритма

42

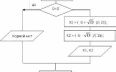
ВЫБОР I
ПРИ 1	: X	= Sin( X );
ПРИ 2	: X	= tas( X );
ПРИ 3	: X	= Exp( X );
ПРИ 4	: X	= Ln( X )
ВСЕ;

КОНЕЦ.

Пример 2.

43

ВЫБОР I
ПРИ 1	X := Sin( X );
ПРИ 2	X := tas( X );
ПРИ 3	X := Exp( X );
ПРИ 4	X := Ln( X )

ИНАЧЕ

ВЫВОД ( ' Значение индекса выбора не соответствует заданным константам .' );

ВСЕ

КОНЕЦ.

4. Организация итерационных циклических процессов

Краткие сведения из теории. Большинство вычислительных процессов обладает следующей особенностью: отдельные участки

вычислений повторяются многократно, при этом всякий раз используются новые значения исходных данных.

Такие вычислительные процессы называют циклическими, а их повторяющиеся участки - циклами.

Применение циклов в программе позволяет эффективно использовать вычислительную машину, приводит к уменьшению длины программы и сокращению времени на ее составление и отладку.

Циклы бывают арифметическими и структурными. Арифметические циклы связаны, в основном, с изменением одной переменной. Они делятся на два типа: циклы на достижение заданной точности (итерационные) и циклы с известным числом повторений.

Циклический процесс называется итерационным, если заранее неизвестно количество повторений цикла, а конец вычисления определяется при достижении некоторой величиной заранее заданной точности вычисления.

Примерами итерационных циклов являются вычисления:

• корней алгебраических и трансцендентных уравнений численными методами;

• корней линейных алгебраических и нелинейных уравнений;

• вычисление квадратного корня по итерационной формуле и т.д.

При программировании итерационных процессов принято их разделять

на циклы с "предусловием" и с "постусловием". Их отличие заключается в том, что проверка достижения некоторой величиной заданной точности вычисления осуществляется соответственно либо в начале цикла, либо в конце цикла. Особенность цикла с "постусловием" заключается в том, что повторяющийся участок алгоритма выполнится хотя бы один раз, в то время как в цикле с "предусловием" этот участок может не выполниться ни разу.

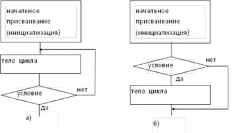
Для графического изображения итерационных процессов используется блок "условие". Функциональная схема итерационных процессов с "постусловием" приведена на рисунке 2.9,а) и с "предусловием" - на рисунке 2.9,б).

44

Инициализация представляет собой задание начальных значений переменным, которые используются в теле цикла.

Тело цикла - это последовательность действий, которые выполняется многократно.

Для записи итерационных процессов имеется два вида операторов цикла:

1. оператор с предварительным условием (предусловием);

2. оператор цикла с последующим условием (постусловием).

Операторы для записи циклов являются сложными, так как в их состав

входят другие операторы.

Для всех операторов цикла характерны следующие особенности:

• повторяющиеся вычисления записываются лишь один раз;

• вход в цикл возможен только через его начало;

• переменные оператора цикла должны быть определены до входа

в циклическую часть;

• необходимо предусмотреть выход из цикла: или по

естественному его окончанию, или по оператору перехода. Если этого не

предусмотреть, то циклические вычисления будут повторяться бесконечно и это приведет к "зацикливанию" программы.

Рисунок 2.9. Функциональная схема итерационных циклов.

2.4.1 Оператор цикла с предварительным условием

Синтаксис оператора цикла с "предусловием":

НЦ ПОКА <логическое выражение>

<предложения тела цикла>

КЦ

Здесь ПОКА (WHILE) - служебное слово, НК и КЦ - операторные скобки, указывают начало и конец цикла соответственно.

Оператор цикла действует следующим образом. Предварительно проверяется значение логического выражения. Пока оно истинно, выполняются предложения циклической части. Как только оно становится ложным, происходит выход из цикла. Если с самого начала значение логического выражения ложно, то предложения циклической части не выполнятся ни разу.

Обратите внимание на то, что предложения циклической части, заключенные в операторные скобки НЦ и КЦ, представляют собой составной оператор.

45

Пример. Словесная постановка задачи. Вычислить приближенное значение суммы S=1/ i с точностью до Eps. При этом i может принимать целочисленные значения с заданным шагом. Дано: Eps - точность приближения; Step - шаг изменения переменной i; iStart - начальное значение переменной i. Результат: S - приближенное значение суммы. Промежуточные данные: а - текущее значение слагаемого 1/ i. Текстуальное описание алгоритма. ввод значений переменных iStart, Step, Eps; S = 0; i = iStart; a = 1/iStart; если a < Eps, перейти на п.10; S = S + a; i = i + Step; a = 1/ i; перейти на п.5; вывод результата. Схема алгоритма. Г рафическая схема алгоритма приведена на рисунке 2.10 ^ Hat	ало}
/ ввод Eps,	Step.
S=0, i=iStart
a = l/iStart

нет

а < Eps

f да Г ]

^ВЬ|В0Д

/ оезультат I

I

i = i + Step а = 1/1 ( ^И°^Н-^Ц )

Рисунок 2.10 - Принципиальная схема циклического алгоритма с "предусловием"

Запись алгоритма на псевдокоде (операторная запись алгоритма).

НАЧАЛО

ВЫВОД('Введите значения переменных iStart, Step, Eps:');

ВВОД(iStart, Step, Eps);

{ инициализация }

46

	1-й шаг	2-й шаг	3-й шаг	4-й шаг	5-й шаг	6-й шаг
i	2	4	6	8	10	12
a	0.5	0.25	0.1999	0.125	0.01	0.0083
S	0.5	0.75	0.9499	1.0749	1.0849	-
a >= Eps	0.5>=0.01	0.25>=0.01	0.1999>=0.01	0.125>=0.01	0.01>=0.01	0.0083>=0.0 1
Значение условия	Истинно	Истинно	Истинно	Истинно	Истинно	Ложно

Таким образом, предложения, составляющие тело цикла, выполнились пять раз. На шестом шаге вычислений, при i=12 и а=0.0083, логическое выражение становится ложным, и управление передается за пределы цикла.

47

2. Оператор цикла с последующим условием

Синтаксис оператора цикла с "постусловием" :

ВЫПОЛНЯТЬ < предложения тела цикла >

ПОКА < логическое выражение > ; .

Здесь ВЫПОЛНЯТЬ и ПОКА - служебные слова.

Оператор с "постусловием" работает следующим образом. Предложения циклической части выполняются повторно (по крайней мере один раз) до тех пор, пока значение логического выражения ложно. Условием прекращения циклических вычислений является истинное значение логического выражения. Итак, сначала выполняется циклическая часть, а затем проверяется условие. Обратите внимание, что эти действия прямо противоположны действиям оператора цикла с "предусловием", где сначала проверяется условие, а затем выполняются предложения циклической части.

Следует подчеркнуть, что нижняя граница предложений циклической части четко обозначена словом ПОКА, поэтому нет необходимости заключать предложение циклической части в скобки вида НЦ - КЦ.

Если в циклической части встречается оператор перехода, указывающий на метку за пределами цикла, то цикл может завершиться до его естественного окончания.

Рассмотрим использование данного оператора на предыдущем примере. Основные изменения претерпевают только схема алгоритма и программа, поэтому рассмотрим только их.

Схема алгоритма

^ конец ^

Рисунок 2.11 - Принципиальная схема циклического алгоритма с "постусловием".

48

	1-й шаг	2-й шаг	3-й шаг	4-й шаг	5-й шаг	6-й шаг
i	2	4	6	8	10	12
a	0.5	0.25	0.1999	0.125	0.01	0.0083
S	0.5	0.75	0.9499	1.0749	1.0849	-
a < Eps	0.5<0.01	0.25<0.01	0.1999<0.01	0.125<0.01	0.01<0.01	0.0083<0.01
Значение условия	Ложно	Ложно	Ложно	Ложно	Ложно	Истинно

Предложения, составляющие тело цикла, выполнились снова пять раз. На шестом шаге вычислений, при i=12 и a=0.0083, логическое выражение становится истинным, и управление передается за пределы цикла.

Примечание: Как видно из примеров, использование оператора с "постусловием" сократило программу на одно предложение и пару операторных скобок.

49

Задания для самостоятельного выполнения.

Вариант 1.

1. Запишите данное математическое выражение на алгоритмическом языке (возведение в степень обозначим через значок ^А):

B = arctg (

x

■Jl^x²' 2

2. Составьте блок -схему алгоритма для вычисления объем V шара, по заданному радиусу R.

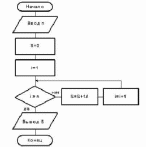
3. Внимательно изучите блок-схему алгоритма. Определите значение S после выполнения алгоритма при n=4.

Вариант 2.

Внимательно просмотрите псевдокод. Определите значение переменной d после выполнения алгоритма.

2. Составьте блок-схему нахождения в заданной последовательности из 10 натуральных чисел числа кратные 3 и 5.

3. Запишите математическое выражение на алгоритмическом языке:

• = e^{sm x} cos x

Вариант 3.

1. Запишите математическое выражение на алгоритмическом языке( возведение в степень обозначим через значок А):

1

• =

i - ¹

a + b

2. Внимательно изучите блок-схему алгоритма.

50

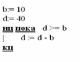
Определите результат выполнения алгоритма, если значения А и В заданы соответственно 25 и 5. Сколько раз выполняется цикл? Что определяется по данному алгоритму?

3. Дано натуральное число N. Составьте блок-схему определения, является ли данное число простым. Простым называется число, которое имеет один делитель равный ему самому.

Вариант 4.

1. Внимательно изучите блок-схему фрагмента алгоритма.

Определите, что ищется по заданному алгоритму.

2. Составьте блок-схему перевода температуры из шкалы Цельсия в шкалу Фаренгейта для заданного диапазона температур. Формула преобразования:

180

Температура по Фаренгейту = (температура по Цельсию) • + 32

3. Запишите математическое выражение на алгоритмическом языке( возведение в степень обозначим через значок ^А):

а^ь *2 + 3.456у Вариант 5.

1. Внимательно просмотрите псевдокод. Определите значение Y в результате выполнения алгоритма, если при вводе были заданы значения :10, 3, 14, 4.

2. Внимательно изучите блок-схему алгоритма.

51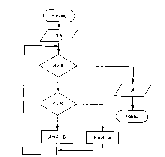

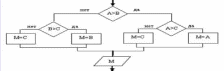
Определите последовательность выполнения блоков алгоритма и значения Х1 и Х2, если введены числа -4, 4, 1.

3. Составьте блок-схему алгоритма вычисления произвольной целочисленной степени числа по ее словесной записи:

1. ввести значения x и n;

2. присвоить z₀ начальное значение 1;

3. присвоить вспомогательной переменной i начальное значение 0;

4. присвоить z результат выполнения операции z*x;

5. присвоить переменной i значение суммы i+1;

6. если i<n, перейти к шагу 4), иначе - остановить работу алгоритма.

Вариант 6.

1. Внимательно просмотрите псевдокод. Определите значение переменной d после выполнения фрагмента алгоритма.

2. Вводиться последовательность ненулевых чисел, 0 - конец

последовательности. Составьте блок-схему для определения: содержит ли последовательность хотя бы два соседних числа с одинаковыми знаками. (Произведение двух чисел с одинаковыми знаками - есть положительное число).

3. Внимательно просмотрите псевдокод. Какие числа будут выведены в результате выполнения алгоритма.

алг «Вывод чисел» нц для i:=2 до б

52

Вариант 7.

1. Внимательно просмотрите псевдокод. Известно, что в результате работы данного алгоритма переменная Y приняла значение 5. Определите, каким было заданно значение переменной X.

• X

Y

X - 5

2 * (Y + 1) X + Y

вывод Y

Запишите данное математическое выражение на алгоритмическом

языке( возведение в степень обозначим через значок ^А):

• 2

. Sin X _ _ , 4/5 x.

А = — + 0.5( x +—)

cos y y

Задана числовая последовательность из десяти натуральных чисел. Составьте блок-схему алгоритма определения количества чётных чисел в заданной числовой последовательности.

Вариант 8.

Заданы значения двух сторон прямоугольного треугольника. Составьте блок-схему вычисления гипотенузы треугольника.

Внимательно изучите фрагмент блок-схемы. Определите, каким будет результат выполнения алгоритма, если переменная Х=14

3. Составьте блок-схему алгоритма, вычисляющего сумму только 5 отрицательных чисел, вводимых с клавиатуры( хотя числа вводятся и положительные и отрицательные в любом порядке и количестве). Вариант 9.

1. Запишите данное математическое выражение на алгоритмическом языке( возведение в степень обозначим через значок а): Y=e^x +|x| + x²

2. Внимательно просмотрите псевдокод. Определите, что выполняет данный фрагмент алгоритма:

ЕСЛИ X =: V ТО

ECJHI X «с Z ТО М := X ИНАЧЕ М = Z ВСЕ ИНАЧЕ

ЕС ЛИ Y =: Z ТО М := V ИНАЧЕ JV1 = Z ВСЕ ВСЕ

3. Дан одномерный массив С(5). Составьте блок-схему алгоритма вычисления произведения для положительных элементов массива С. Вариант 10.

53

1. Внимательно просмотрите псевдокод (операция mod(x,y) - получение остатка целочисленного деления x на у). Определите значение переменной d после выполнения этого фрагмента алгоритма:

к := 70 выб О]*

| гл>и mocI( 1с, 12 > = 7

| щ>и 11юс1( 1^- 12 ) < 5

| иди iiiocl( к, 12 ) > 9

| 1шп^ж1е

все

2. Запишите данное математическое выражение на алгоритмическом языке(

D

• = ^— + A^x+¹

возведение в степень обозначим через значок а): ^x +¹

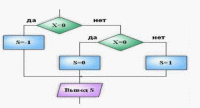
3. Дано число Х. Если его значение положительное, извлечь квадратный корень из числа Х. Если число Х отрицательное, то возвести его в квадрат. Составьте блок-схему алгоритма для решения данной задачи.

cl := к:

cl 2,1 cl := 3; ct := 1

54