МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Восточно-Сибирский государственный университет технологий и управления»

Кафедра «Системы информатики»

Методические рекомендации по выполнению индивидуальных заданий по дисциплине «теоретические основы информатики» для студентов заочной формы обучения

Составитель: Базарон С.А.

Улан-Удэ, 2013

Порядок выполнения контрольной работы

В лабораторном практикуме по дисциплине «Теоретические основы информатики» в конце каждой темы приведены задания для самостоятельного выполнения. Выберите свой вариант и выполните его.

Для успешного выполнения контрольной работы вначале изучите теоретический материал, разберите примеры решения подобных задач.

Порядок выбора номера варианта контрольной работы

Вариант контрольной работы выбирается по последним двум цифрам зачетной книжки. Например, если номер зачетной книжки Б662-003, то номер варианта 3.

По каждой теме десять вариантов индивидуальных заданий, поэтому если номер зачетной книжки превышает число 10, то от последних двух цифр зачетной книжки нужно отнять 10. Если в результате вычитания получилось число большее 10, то процедуру вычитания необходимо повторять до получения числа меньшего 10. Например, если номер зачетной книжки Б662-032, то номер варианта вычисляется следующим образом: 32-10=22-10=12- 10=2, т.е. номер варианта 2.

Требования к оформлению контрольных работ

Структура оформления контрольной работы:

1. Титульный лист, оформляется в соответствии с Приложением 1

2. Содержание.

3. Основная часть:

Раздел 1. Основы теории информации

1. Меры и единицы количества и объема информации. Использование формул Хартли и Шеннона.

2. Системы счисления. Представление и обработка в компьютере вещественных чисел.

3. Основные понятия алгебры высказываний

4. Логические основы ЭВМ.

Раздел 2. Основы алгоритмизации. Программирование.

4. Список литературы.

Разрешается два варианта оформления контрольной работы:

1. В виде документа MS Word. При этом используется шрифт 12 - 13 пт, 1,5 интервал, выравнивание по ширине, абзацный отступ 1,25.

2. В тетради в клетку.

2

Приложение 1

Министерство образования и науки РФ ФГБОУ ВПО «Восточно-Сибирский государственный университет

технологий и управления»

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Теоретические основы информатики» студента заочной формы обучения направления подготовки ... «...»

Выполнил: Ф.И.О

Улан-Удэ, год

3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ Кафедра систем информатики

ЛАБОРАТОРНЫЙ ПРАКТИКУМ по дисциплине «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ» для студентов заочной формы обучения

Улан-Удэ, 2013

4

Оглавление

Раздел 1. Основы теории информации 6

1. Меры и единицы количества и объема информации. Использование формул Хартли и

Шеннона 6

Задания для самостоятельного выполнения 13

2. Системы счисления. Представление и обработка в компьютере вещественных чисел 15

Представление и обработка в компьютере вещественных чисел 19

Задания для самостоятельного выполнения 22

3. Основные понятия алгебры высказываний 24

Задания для самостоятельного выполнения 26

4. Логические основы ЭВМ 30

Задания для самостоятельного выполнения 33

Раздел 2. Основы алгоритмизации. Программирование 35

Задания для самостоятельного выполнения 53

5

Раздел 1. Основы теории информации

1. Меры и единицы количества и объема информации. Использование формул Хартли и Шеннона.

Количество информации измеряется размером двоичного кода, с помощью которого эта информация представлена

Поскольку любые виды информации представляются в компьютерной памяти в форме двоичного кода, то это определение универсально. Оно справедливо для символьной, числовой, графической и звуковой информации.

Один знак (разряд) двоичного кода несет 1 бит информации.

Бит (binary digit) - минимальная единица измерения информации, которая представляет собой двоичный знак двоичного алфавита {0;1}.

Байт (bate) - единица количества информации в СИ, представляющая собой восьмиразрядный двоичный код, с помощью которого можно представить один символ. 1 байт = 8 бит

Информационный объем сообщения (информационная емкость сообщения) - количество информации в сообщении, измеренное в стандартных единицах или производных от них (Кбайтах, Мбайтах и т.д.).

1 байт = 8 бит

1 Кбайт = 210 байт = 1024 байт

1 Мбайт = 210 Кбайт = 220 байт

1 Гбайт = 210 Мбайт = 220 Кбайт = 230 байт

В теории информации количеством информации называют числовую характеристику сигнала, не зависящую от его формы и содержания, и характеризующую неопределенность, которая исчезнет после получения сообщения в виде данного сигнала. В этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.

Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность равна 1) количество информации в сообщении о нем равно 0. Чем неожиданное событие, тем больше информации он несет.

Лишь при равновероятных событиях: ответ «да» или «нет», несет 1 бит. Количество информации. Формулы Хартли и Шеннона В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Предложенная им формула имела следующий вид:

I = log2 K ,

где K - количество равновероятных событий; I - количество бит в сообщении, такое, что любое из K событий произошло. Тогда K=2^I. Иногда формулу Хартли записывают так:

I = log2K = log2 (1 / р) = - log2 р, т. к. каждое из K событий имеет равновероятный исход р=1/£, то K=1^. Пример 1. Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В.

Решение. Такое сообщение содержит I=log₂ 3 = 1,585 бита информации.

6

Но не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или "правило бутерброда".

"Однажды в детстве я уронил бутерброд. Глядя, как я виновато вытираю масляное пятно, оставшееся на полу, старший брат успокоил меня:

• не горюй, это сработал закон бутерброда.

• Что еще за закон такой? - спросил я.

• Закон, который гласит: "Бутерброд всегда падает маслом вниз". Впрочем, это шутка, - продолжал брат.- Никакого закона нет. Просто бутерброд действительно ведет себя довольно странно: большей частью масло оказывается внизу.

• Давай-ка еще пару раз уроним бутерброд, проверим, - предложил я. - Все равно ведь его придется выкидывать.

Проверили. Из десяти раз восемь бутерброд упал маслом вниз.

И тут я задумался: а можно ли заранее узнать, как сейчас упадет бутерброд маслом вниз или вверх?

Наши опыты прервала мать." ( Отрывок из книги "Секрет великих полководцев", В.Абчук).

В 1948 г. американский инженер и математик К Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями. Если I - количество информации, K - количество возможных событий, рi - вероятности отдельных событий, то количество информации для событий с различными вероятностями можно определить по формуле:

I = - Е р log2 р_ь

где i принимает значения от 1 до K.

Формулу Хартли теперь можно рассматривать как частный случай формулы Шеннона:

I = - Е 1 / К log2 (1 / К) = I = log2 К.

При равновероятных событиях получаемое количество информации максимально.

Пример 2. Определить количество информации, получаемое при реализации одного из событий, если бросают

а) несимметричную четырехгранную пирамидку;

б) симметричную и однородную четырехгранную пирамидку.

Решение.

а) Будем бросать несимметричную четырехгранную пирамидку. Вероятность отдельных событий будет такова:

р1 = 1/2, р2 = 1/4, р3 = 1/8, р4 = 1/8,

тогда количество информации, получаемой после реализации одного из этих событий, рассчитывается по формуле:

I = -(1/2 log₂ 1/2 + 1/4 log₂ 1/4 + 1/8 log₂ 1/8 + 1/8 log₂ 1/8) = 1/2 + 2/4 + 3/8 + 3/8 = 14/8 = 1,75 (бит).

7

б) Теперь рассчитаем количество информации, которое получится при бросании симметричной и однородной четырехгранной пирамидки:

I = log₂ 4 = 2 (бит).

Приме 3. Сколько различных чисел можно закодировать с помощью 8 бит?

Решение: I=8 бит, K=2^I=2⁸=256 различных чисел.

При передаче и хранении информации с помощью различных технических устройств информацию следует рассматривать как последовательность знаков (цифр, букв, кодов цветов точек изображения), не рассматривая ее содержание.

Считая, что алфавит (набор символов знаковой системы) - это событие, то появление одного из символов в сообщении можно рассматривать как одно из состояний события. Если появление символов равновероятно, то можно рассчитать, сколько бит информации несет каждый символ. Информационная емкость знаков определяется их количеством в алфавите. Чем из большего количества символов состоит алфавит, тем большее количество информации несет один знак. Полное число символов алфавита принято называть мощностью алфавита.

Молекулы ДНК (дезоксирибонуклеиновой кислоты) состоят из четырех различных составляющих (нуклеотидов), которые образуют генетический алфавит. Информационная емкость знака этого алфавита составляет:

4. = 2¹, т.е. I = 2 бит.

Каждая буква русского алфавита (если считать, что е=е) несет информацию 5 бит (32 = 2¹).

При таком подходе в результате сообщения о результате бросания кубика, получим различное количество информации. Чтобы его подсчитать, нужно умножить количество символов на количество информации, которое несет один символ.

Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении.

Задачи на определение количества информации.

З-1. Текстовое сообщение, содержащее 1048576 символов общепринятой кодировки, необходимо разместить на дискете ёмкостью 1,44Мб. Какая часть дискеты будет занята?

Дано:

K=1048576 символов;

i=8 бит/символ

Решение:

V=K*i=1048576*8=8388608 бит=1048576 байт=1024 Кб=1Мб,

что составляет 1Мб*100%/1,44Мб=69% объёма дискеты

Ответ: 69% объёма дискеты будет занято переданным сообщением.

8

З-2. Информация в кодировке Unicode передается со скоростью 128 знаков в секунду в течение 32 минут. Какую часть дискеты ёмкостью 1,44Мб займёт переданная информация?

Дано:

v=128 символов/сек;

t=32 минуты=1920сек; i=16 бит/символ

Решение:

К^^=245760символов

У=К^=245760*16=3932160бит=491520байт=480 Кб=0,469Мб, что составляет 0,469Мб*100%/1,44Мб=33% объёма дискеты Ответ: 33% объёма дискеты будет занято переданным сообщением З-З. Видеопамять компьютера имеет объем 512 Кб, размер графической сетки 640х200, в палитре 16 цветов. Какое количество страниц экрана может одновременно разместиться в видеопамяти компьютера?

Дано:

К=640х200=128000 пикселей;

N=16 цветов;

Увп=512 Кб Решение:

Используем формулы

V=K*i; N=2ⁱ; m= Увп/V,

где m - это количество страниц экрана

16=2⁴ & i=4 бита/пиксель;

K=640 '200=128000пикселей

V=128000*4=512000бит=64000байт=62,5Кб на один экран M=512/62,5=8 страниц

Ответ: 8 полных страниц экрана можно одновременно хранить в видеопамяти компьютера

З-4. В результате преобразования растрового графического

изображения количество цветов уменьшилось с 256 до 16. Как при этом изменится объем видеопамяти, занимаемой изображением?

Дано:

N₁=256 цветов;

N₂=16 цветов;

Решение:

Используем формулы

V1=K*i1; N1=2ⁱ¹; V2=K*i2; N2=2ⁱ²;

N₁=256=2⁸; & i₁=8 бит/пиксель N₂=16=2⁴; & i₂=4 бит/пиксель V₁=K*8; V₂=K*4;

• 2/V1=4/8=1/2

Ответ: объём графического изображения уменьшится в два раза.

З-5. Сканируется цветное изображение стандартного размера А4 (21*29,7 см). Разрешающая способность сканера 1200dpi и глубина цвета 24 бита. Какой информационный объём будет иметь полученный графический файл?

9

Дано:

i=24 бита на пиксель;

S= 21см*29,7 см

D=1200dpi (точек на один дюйм)

Решение:

Используем формулы V=K*i;

1дюйм=2,54 см

S=(21/2,54)*(29,7/2,54)=8,3дюймов* 11,7дюймов K=1200*8,3*1200*11,7=139210118 пикселей

V=139210118*24=3341042842бита=417630355байт=407842Кб=398Мб

Ответ: объём сканированного графического изображения равен 398 Мегабайт

З-6. На шахматной доске в одной из клеток произвольным образом поставлена фигура. Априори все положения фигуры на доске одинаково вероятны. Определить информацию, получаемую от сообщения, в какой именно клетке находится фигура.

Решение: Энтропия системы Xс n равновероятными состояниями равна log n; в данном случае

I_X=H(X)=log64=6

Ответ: Сообщение содержит 6 двоичных единиц информации. Так как все состояния системы равновероятны, то ту же информацию несет и любое конкретное сообщение типа: фигура находится в квадрате e .

З-7. В условиях задачи 6 определить частную информацию от сообщения, что фигура находится в одной из угловых клеток доски.

Решение: Априорная вероятность состояния, о котором сообщается,

равна

_ ⁴ _ ¹

^Р ~ 64 “ 16 .

Ответ: Частная информация равна

З-8. Определить частную информацию, содержащуюся в сообщении впервые встреченного лица A: «сегодня мой день рождения».

Решение: Априори все дни в году с одинаковой вероятностью могут

быть днями рождения лица А Вероятность полученного сообщения 365 .

Ответ: Частная информация от данного сообщения равна примерно 8 бит информации.

З-9. В условиях примера 3 определить полную информацию от сообщения, выясняющего, является ли сегодняшний день днем рождения впервые встреченного лица Л-.

10

Решение: Система, состояние которой выясняется, имеет два возможных состояния: х\ - день рождения и х2 - не день рождения. 1 Pi = ^77 Р2 364 Вероятности ЭТИХ СОСТОЯНИЙ ’ * 365 ; 365 . Ответ: Полная информация равна примерно 0,063 бит информации. З-10. По цели может быть произведено n независимых выстрелов; вероятность поражения цели при каждом выстреле равна p. После k-го выстрела (1<=k<n) производится разведка, сообщающая, поражена или не поражена цель; если она поражена, стрельба по ней прекращается. Определить к из того условия, чтобы количество информации, доставляемое разведкой, было максимально. Решение: Рассмотрим физическую систему Хк - цель после к-го выстрела. Возможные состояния системы Хк будут х1 - цель поражена; х2 - цель не поражена. *	ч	ч
д		(1 -rt

Очевидно, информация, доставляемая выяснением состояния системы Хк, будет максимальна, когда оба состояния Л'| и jc₂ равновероятны:

откуда

где ^log - знак двоичного логарифма.

Например, при р=0,2 получаем (округляя до ближайшего целого числа)

к = —-— я 3

1. 3219 _

З-11. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Кбайта.

Решение: Информационный объем сообщения переведем в биты:

1= 1,25 Кбайт = 10 240 бит

Определим количество бит, приходящееся на один символ сообщения:

10240/2048 = 5 бит

Определим количество символов в алфавите:

N = 2¹ = 2⁵ = 32

Ответ: В алфавите 32 символа.

Если информация выражена в двоичных единицах, то ей можно дать довольно наглядное истолкование, а именно: измеряя информацию в двоичных единицах, мы условно характеризуем ее числом ответов «да» или

11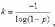

*	*1	ч
д	й	Р2