LEKTsIYa_7

ЛЕКЦИЯ 7

ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

Если задана произвольная функция, то ее производная является функцией того же аргумента х. Поэтому можно ставить вопрос об отыскании производной от производной. Производная от производной – это производная второго порядка.

- первая производная

- вторая производная

Первая производная – это скорость движения

,

Вторая производная

Аналогично:

Примеры:

1.

2. ,

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Запишем связь между приращением всякой дифференцируемой функции и приращением ее аргумента

(1)

Величина , входящая в правую часть этой формулы, является б.м. величиной, т.е. стремится к нулю одновременно с :

Или . В силу этого, слагаемое будет произведение бесконечно малых величин, т.е. будет бесконечно малой более высокого порядка малости по сравнению с . В тоже время - бесконечно малая того же порядка малости, что и (если ). Поэтомубудет называться главной частью приращения функции и, причем, она пропорциональна приращению . Эту главную часть приращения функции, пропорциональной приращению аргумента мы и будем называть дифференциалом :

подставим в (1), получим

Таким образом

1. Дифференциал функции равен произведению ее производной на дифференциал аргумента (независимой переменной).

2. Разность между приращением функции и ее дифференциалом есть величина б.м. более высокого порядка малости по сравнению с .

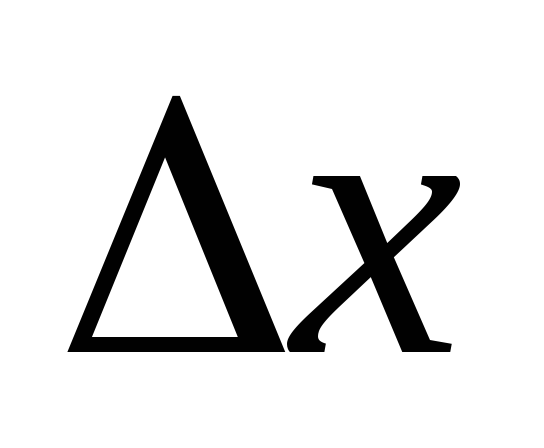3. В силу этого последнего свойства при 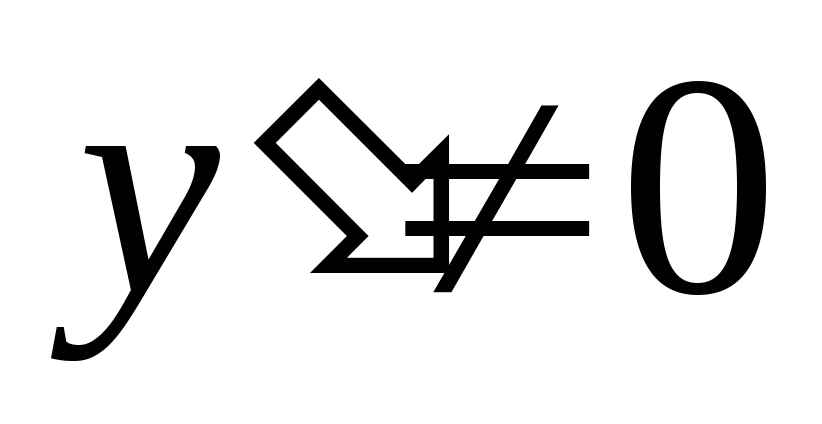приращение функции м ее дифференциал будут при б.м. 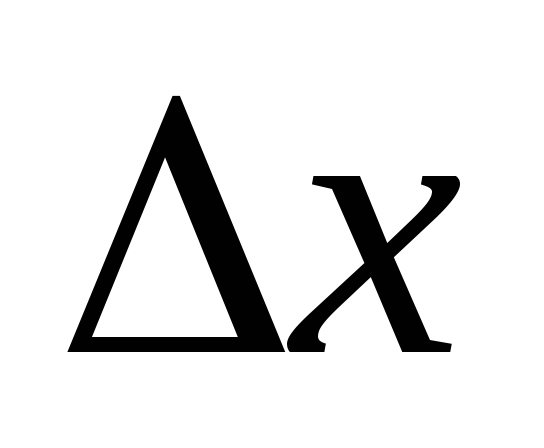равносильными величинами, т.е.

Дифференциал функции имеет простой геометрический смысл. Значение дифференциала функции при данном значении аргумента х и данном приращении равно приращению ординаты касательной, проведенной в точке с абсциссой х графика этой функции, при переходе от точки касания х соседней точке .

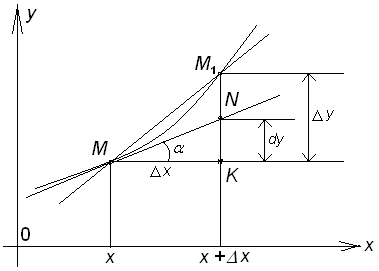
Приращение - катет М₁K, треугольника MМ₁K. Второй катет MK=. Угол между касательной в т.х и осью ох – угол , причем ;

ДИФФЕРЕНЦИАЛ СЛОЖНОЙ ФУНКЦИИ

Дифференциал сложной функции равен производной этой функции по промежуточному аргументу на дифференциал этого аргумента.

Пусть

По правилу дифференцирования сложной функции, имеем

умножим на

Таким образом, дифференциал обладает свойством инвариантности, т.е. свойством неизменности формы записи дифференциала, как для случая простой, так и сложной функции.

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ, ЗАПИСАННЫЕ В ДИФФЕРЕНЦИАЛАХ

1.

2.

3.

4.

5.

ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ, ЗАПИСАННЫЕ В ДИФФЕРЕНЦИАЛАХ

2.

3.

4.

5.

6.

7.

ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Дифференциалом второго порядка от функции называется дифференциал ее дифференциала

Дифференциал п-ого порядка

ПРАВИЛО БЕРНУЛЛИ-ЛОПИТАЛЯ

Раскрытием неопределенности в мат.анализе называется отыскание предела , когда функция непрерывна вблизи точки х=а, приводят к выражениям вида:

Основными видами неопределенности являются:

Пусть и непрерывны вблизи т.а, но неопределенна в самой точке, тогда:

. Это же правило сохраняется, если

Примеры:

1.

2.

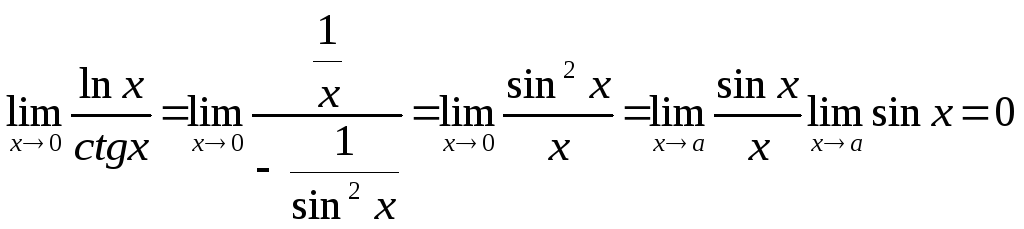
Если вблизи т.а существуют производные и и причем и если существует конечный или бесконечный предел

, то правило Лопиталя дает:

Примеры:

3.

4. Функции представляют собой произведение или разность бесконечно больших и бесконечно малых величин.

сводятся к .

4.

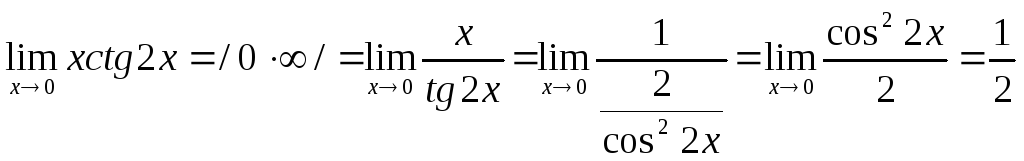
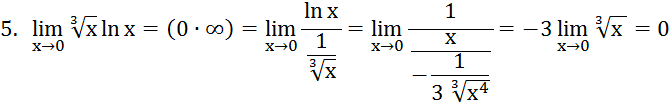
6.

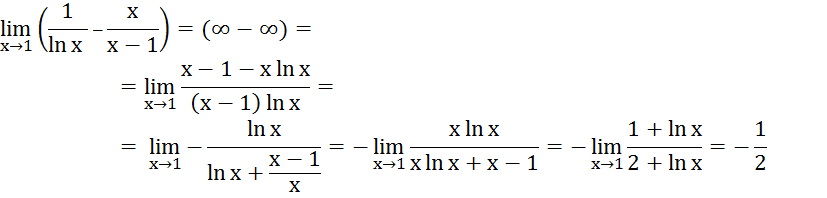
Если неопределенности следующего типа: , функции представляют собой степень в основании которого 1, ∞, 0, а в показателе ∞, 0.Эти неопределенности сводится к неопределенностям вида: к которым применимо правило Лопиталя.

?

обозначим и прологарифмируем

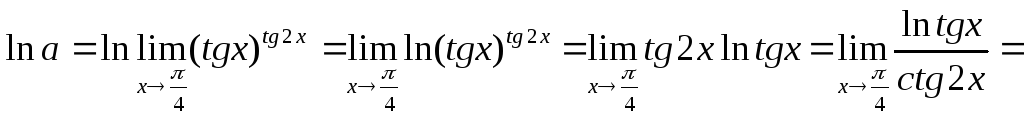
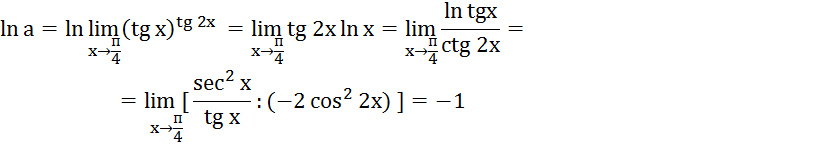
8. обозначим

прологарифмируем

9.обозначим

прологарифмируем