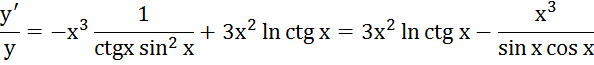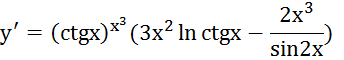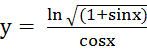LEKTsIYa_6

ЛЕКЦИЯ 6

ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

1) Показательная функция

придадим приращение и найдем .

делим на .

при

Более подробно. Покажем, что

Перейдем к пределу

поэтому

В частности,

2) Логарифмическая функция

, т.к. - б.м., а по второму замечательному пределу , то имеем

В виду непрерывности логарифмической функции

Если

3) Производная от степенной функции

, т – целое положительное число

Разложим по биному Ньютона

при все слагаемые, кроме первого стремятся к нулю.

4) Производные тригонометрических функций

;

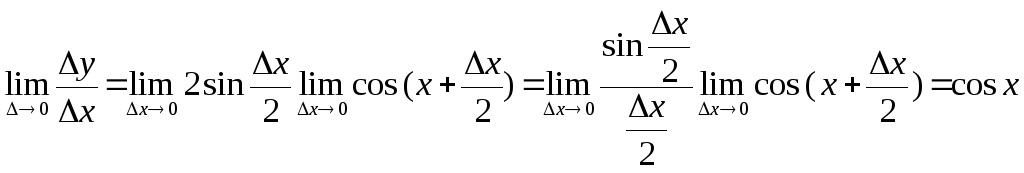
5).

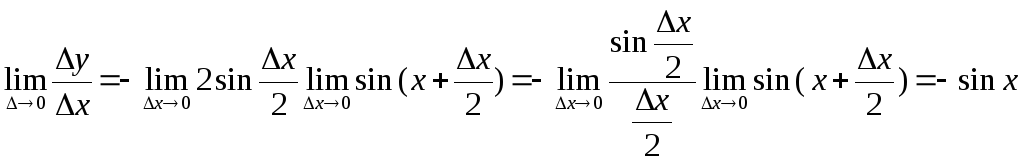
6). , или - возьмем производную частного

7).

Производная сложной функции

Пусть заданы функции , каждая из которых дифференцируема по своему аргументу. При наличии общей области определения можно записать у как сложную функцию аргумента х.

.

Докажем, что

Доказательство:

В силу дифференцируемости функции у имеем

здесь б.м., одновременно с , т.е.

. Аналогично, для , - б.м.

Подставляем

при перейдем к пределу

Правило дифференцирования сложной функции без труда распространяется на сложную функцию при любом количестве промежуточных аргументов.

Примеры:

1.

2.

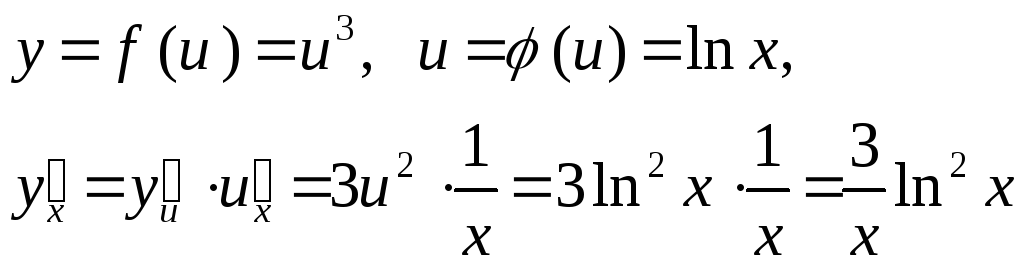
3.

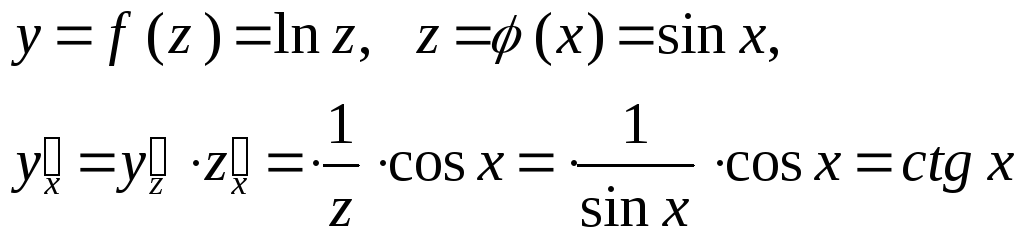
Правила дифференцирования

1.

2.

3.

4.

5.

6.

7.

8.

Формулы дифференцирования

1.

2.

3.

4.

5.

6.

7.

Таблица дифференцирования сложных функций

1.

2.

3.

4.

5.

6.

7.

Примеры на отыскания производной

1.

2.

3.

4.

5.

6.

,

7. 

7. 

7. 

7. 

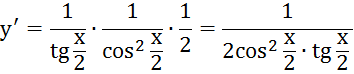
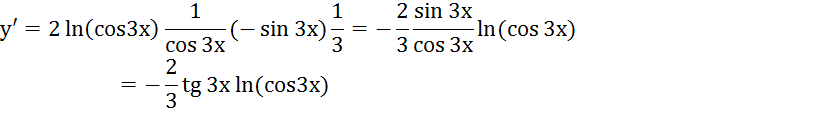
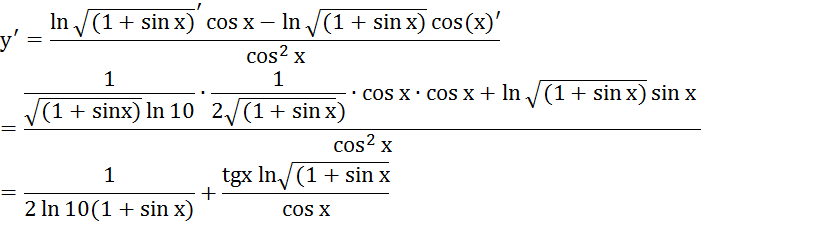
или, воспользуемся свойствами логарифмов, имеем , тогда производная упрощается:

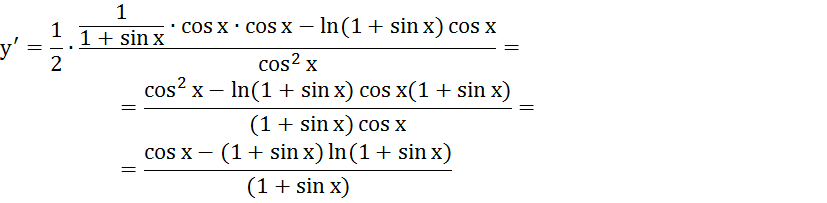
Дифференцирование функций, заданных неявно

Пусть зависимость между аргументом х и функцией у задана уравнением, неразрешенным относительно у. Такая зависимость называется неявной.

Например:

Тогда, для отыскания производной неявной функции, надо продифференцировать уравнение по простой переменной х, рассматривая при этом у как функцию от х.

Примеры:

1.

2.

3. 

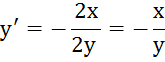
Дифференцирование функций, заданных параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически при помощи функций

Будем предполагать, что дифференцируемые функции параметра t, причем. Как всякие дифференцируемые функции, будут непрерывны. В силу этого при одновременно стремятся к нулю и и .

Найдем .

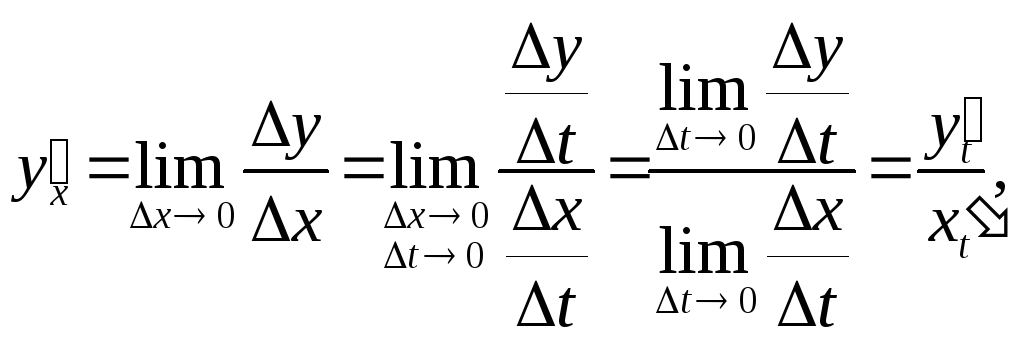т.о., если , то

Примеры.

1.

дифференцируем по t:

, тогда

.

2.

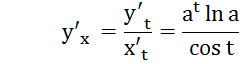
Логарифмическое дифференцирование

Метод логарифмического дифференцирования заключается в том, что от заданной функции у предварительно находится натуральный логарифм, а затем функция дифференцируется.

Найдем производную от показательной функции

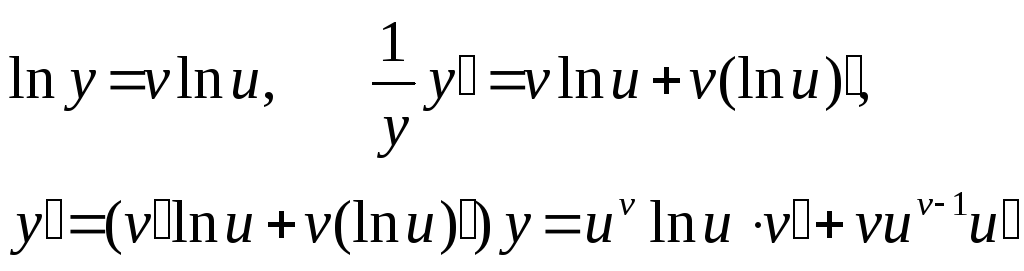
Примеры:

1.

Прологарифмируем:

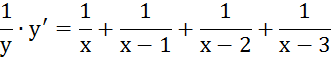
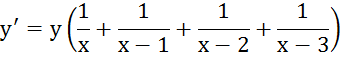
2.

Прологарифмируем:

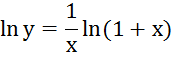
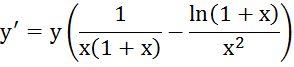
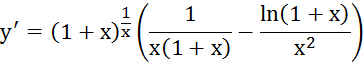
3.

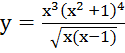
Прологарифмируем:

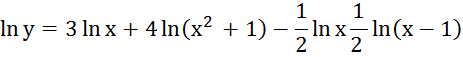
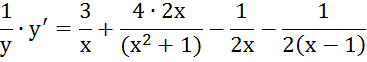
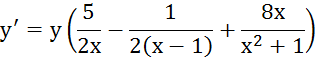
4.

Прологарифмируем: