
Лабораторные работы по программированию на языке С++
.pdfАлексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
4 |
Содержание |
|
Лабораторная работа №1. |
|
Тема: «Программирование линейных вычислительных процессов» .................................. |
5 |
Лабораторная работа №2. |
|
Тема «Программирование разветвляющихся вычислительных процессов» ..................... |
7 |
Лабораторная работа №3. |
|
Тема «Условный оператор в С++. Вычисление значения функции, проверка попадания |
|
точки в область на плоскости» ................................................................................................ |
9 |
Лабораторная работа №4. |
|
Тема «Программирование циклических вычислительных процессов с варьируемым |
|
параметром цикла» ................................................................................................................ |
13 |
Варианты заданий .................................................................................................................. |
19 |
Лабораторная работа №7. |
|
Тема «Применение функций для решения нелинейных уравнений» ............................... |
22 |
Лабораторная работа № 8. |
|
Тема «Обработка одномерных массивов» .......................................................................... |
23 |
Лабораторная работа № 9 |
|
Тема «Указатели и динамические массивы. Использование указателей в качестве |
|
аргументов функций» ............................................................................................................. |
25 |
Лабораторная работа № 10. |
|
Тема «Обработка двумерных массивов» ............................................................................. |
28 |
Лабораторная работа № 11. |
|
Тема «Программирование задач линейной алгебры» ........................................................ |
31 |
Лабораторная работа № 12 . |
|
Тема «Структуры в С++» ....................................................................................................... |
35 |
Лабораторная работа № 13 . |
|
Тема «Текстовые и двоичные файлы в С++» ...................................................................... |
37 |
Лабораторная работа № 14 . |
|
Тема «Динамические структуры в С++. Текстовые и двоичные файлы» ......................... |
39 |
Лабораторная работа №15. |
|
Тема «Программирование на С++ с использованием классов. Перегрузка операторов» |
|
.................................................................................................................................................. |
45 |
Лабораторная работа №16. |
|
Тема «Программирование на С++ с использованием классов. Массивы объектов . |
|
Наследование» ....................................................................................................................... |
55 |
Список литературы ................................................................................................................. |
61 |
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
5 |
Лабораторная работа №1.
Тема: «Программирование линейных вычислительных процессов»
Цель работы : Изучить структуру программы на языке С++ [1, с. 10-33, с. 47-48]. Ознакомиться с операторами ввода и вывода [1, с. 49-52]. Ознакомиться с программированием математических формул [1, с. 47].
Задание: Написать две программы на языке С++ для расчета значений переменных y и z по заданным формулам (табл. 1.1). В первой программе использовать для ввода функцию scanf, для вывода – функцию printf. Во второй программе использовать операторы потокового ввода-вывода cin и cout. Определить разность между значениями y и z. В программе предусмотреть ввод исходных данных с экрана дисплея. Предварительно вычислите ожидаемые значения y и z с помощью калькулятора. Убедитесь, что значения, вычисленные с помощью калькулятора, совпадают с результатами, которые получаются в результате работы программы.
Таблица 1.1. Варианты заданий к лабораторной работе №1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вариант 1 |
|
|
|
|
|
|
|
Вариант 2 |
|
|
|
|
|
|
||||||||||||
|
sin 2π 3α |
|
|
|
|
|
|
y=cos α sin α cos3α sin3α |
||||||||||||||||||
|
|
|
|
5 |
3 |
|
z=2 |
|
cosα sin |
|
π |
2α |
|
|||||||||||||
|
|
|
|
|
2 |
|||||||||||||||||||||
y=1 −sin 3α−π ; z |
=ctg 4 |
π 2 |
α |
4 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Вариант 3 |
|
|
|
|
|
|
|
Вариант 4 |
|
|
|
|
|
|
||||||||||||
y=sin 2α sin 5α−sin 3α |
|
|
y=sin 2α sin 5α−sin 3α |
|
||||||||||||||||||||||
|
cos α 1 −2 sin2 2α |
|
|
|
cos α−cos3α cos5α |
|
||||||||||||||||||||
z=2sinα |
|
|
|
|
|
|
|
|
z=tg 3α |
|
|
|
|
|
|
|
||||||||||
Вариант 5 |
|
|
|
|
|
|
|
Вариант 6 |
|
|
|
|
|
|
||||||||||||
y=1 −1 sin2 2α cos2α |
|
|
y=cos α cos2α cos6α cos 7α |
|||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
α |
5 |
|
|
|
|
|
|||||||
z=cos2 α cos4 α |
|
|
|
|
|
z=4cos 2 |
cos 2 α cos 4α |
|
||||||||||||||||||
Вариант 7 |
|
|
|
|
|
|
|
Вариант 8 |
|
|
|
|
|
|
||||||||||||
2 |
|
3 |
α |
|
2 |
11 |
α |
|
y=2 sin2 3π−2α cos2 5π 2α |
|||||||||||||||||
y=cos |
8 |
π−4 |
−cos |
8 π 4 |
|
1 |
1 |
|
|
5 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=4 |
−4 sin 2 π−8α |
|
|
|
||||||||
z= |
2 |
sin α |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариант 9 |
|
|
|
|
|
|
|
Вариант 10 |
|
|
1 |
|
|
|
||||||||||||
y= cos α−cos β 2− sin α−sin β 2 |
|
|
4 |
|
|
2 |
|
|
2 |
|
|
|||||||||||||||
z=−4 sin |
2 α− β |
cos α β |
|
|
y=cos |
a sin |
b 4 sin |
2a−1 |
||||||||||||||||||
2 |
|
|
|
z=sin b a sin b−a |
|
|
||||||||||||||||||||
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
|
6 |
|||||||||||||||||||||||||||||||
Продолжение табл.1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вариант 11 |
Вариант 12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 −2sin2 α |
y= |
sin 4α |
|
cos2α |
|
|
|
|
|
|
|||||||||||||||||||||
y=1 sin3α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 cos 4α |
1 cos 2α |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 −tg α |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z=1 tg α |
z=ctg 2 π−α |
|
|
|
|
|
|
||||||||||||||||||||||||||
Вариант 13 |
Вариант 14 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y=sin α cos 2β−α |
y=1 |
sin α β−γ −sin β γ−α |
|
|
|||||||||||||||||||||||||||||
|
|
cos α−sin 2β−α |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 sin 2β |
sin γ α− β −sin α β γ |
|
|
|
||||||||||||||||||||||||||||
z=cos2β |
z=sin α cos β cosγ |
|
|
|
|
|
|
||||||||||||||||||||||||||
Вариант 15 |
Вариант 16 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2x−3 x 1 |
x2−9 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
y= |
2b 2 b −4 |
|
y= |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
b −4 b 2 |
|
|
|
2x−3 x−1 x |
−9 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
z= |
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
b 2 |
|
|
|
|
|
|
|
|
x−3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вариант 17 |
Вариант 18 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
3 tg α−tg3 α |
|
|
|
|
|
|
|||||||||||||||
y=4 [ cos α β−γ cos β γ−α |
y=1 −3 tg2 α |
|
|
|
|
|
|
||||||||||||||||||||||||||
cos γ α−β cos α β γ ] |
z=tg 3α |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
z=cos α cos β cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Вариант 19 |
Вариант 20 |
|
|
|
|
|
|
|
|
−1 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 −cos α |
|
|
|
|
1 a a2 |
|
1 −a a2 |
|
|
2 |
|
||||||||||||||||
y= 1 cosα |
y= 2a a2 |
2 −2a−a2 |
|
|
5 −2a |
|
|
||||||||||||||||||||||||||
z= |
1 −cosα |
z=4 −a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вариант 21 |
Вариант 22 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 tg α−4 tg3 α |
|
|
|
|
|
|
|||||||||||||
y=8 cos4α 4 cos2α 3 |
y= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 −6 tg2 α tg4 α |
|
|
|
|
|
|
|||||||||||||||||||||||||||
z=cos4 α |
z=tg 4α |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Вариант 23 |
Вариант 24 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y=1 cos4α−4 cos2α 3 |
y=cos α sin α |
|
|
|
|
|
|
||||||||||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
cos α−sin α |
|
|
|
|
|
|
||||||||||||||
z=sin4 α |
z=tg 2α sec2α |
|
|
|
|
|
|
||||||||||||||||||||||||||
Вариант 25 |
Вариант 26 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y=1 [ sin α β−γ sin β γ−α |
y=1 |
3 sin α−sin3α |
|
|
|
|
|
|
|||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin γ α− β −sin α β γ ] |
z=sin3 α |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
z=sin α sin β sin γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
7 |
Лабораторная работа №2.
Тема «Программирование разветвляющихся вычислительных процессов»
Цель работы : Изучение условного оператора в языке С++[1, с. 59-73]. Задание: Составить алгоритм и написать программу на языке С++ решения
задачи согласно своего варианта.
Варианты заданий
1.Задана точка M с координатами (x,y). Определить месторасположение этой точки в декартовой системе координат (является ли эта точка началом координат, лежит на одной из координатных осей или расположена в одном из координатных углов).
2.Задана квадратичная функция вида y=ax2+bx+c. Вывести сообщения, как направлены ветви параболы, сколько у нее точек пересечения с осью ОХ.
3.Задан параллелограмм со сторонами a, b и углом α между ними. Определить тип параллелограмма (ромб, прямоугольник или квадрат), если это возможно.
4.Известны углы α и β у основания трапеции. Выяснить, если это возможно, тип трапеции (прямоугольная, равнобедренная, прямоугольник).
5.Задан круг с центром в точке О(x0, y0) и радиусом R0 и точка А (x1, y1). Определить месторасположение точки по отношению к кругу (находится внутри круга, вне его или лежит на окружности).
6.Определите, пересекаются ли парабола у=cx2+dx+f и прямая y=ax+b. При положительном ответе найти точки пересечения.
7. Заданы три функции y1=x3, y2=x3+1, |
y3= |
1 |
|
. Определить, являются ли эти |
1 x |
2 |
|||
функции четными или нечетными. |
|
|
|
|
|
|
|
|
8.Выяснить, пересекаются ли параболы у=аx2+bx+с и у=dx2+ex + ¦. При положительном ответе найти точки пересечения.
9.Выяснить, пересекаются ли кривые у=аx3+bx2+сx+d и y=ex3+fx2+gx+h. При положительном ответе найти точки пересечения.
10.Определите, пересекаются ли кривая у=аx3+bx2+сx+d и прямая y=fx+g. При положительном ответе найти точки пересечения.
11.Задана окружность с центром в точке О(x0,y0) и радиусом R0 и прямая y=ax+b. Определить, пересекаются ли прямая и окружность. При положительном ответе найти точки пересечения.
12.Заданы две окружности: с центром в точке О(x0, y0) и радиусом R0 и с центром в точке О(x1, y1) и радиусом R1. Определите, во скольких точках пересекаются окружности.
13.Заданы три точки на плоскости: M с координатами (x1,y1), L с координатами (x2,y2) и H с координатами (x3,y3). Определите, лежат ли они на одной прямой. При отрицательном ответе найти площадь и периметр треугольника MLH.
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
8 |
14.Заданы три точки А(a1,a2,a3), В(b1,b2,b3) и С(c1,c2,c3). Определить, между какими точками расстояние будет наименьшим.
15.Задан треугольник с углами α, β и γ. Определить тип треугольника — остроугольный, прямоугольный или тупоугольный.
16.Заданы точки А(a1,a2) и В(b1,b2). Определить, лежат ли они на прямой y=ax+b.
17.Известны уравнения двух прямых y=a1x+b1 и y=a2x+b2. Определить, являются ли эти прямые параллельными или перпендикулярными, если нет, то найти угол между ними.
18.Задан треугольник со сторонами a, b и с. Определить, является ли этот треугольник равносторонним, равнобедренным, если нет, вычислить площадь треугольника.
19.Даны уравнения двух прямых y=a1x+b1 и y=a2x+b2. Определить, пересекаются ли эти прямые, совпадают или параллельны.
20.Даны 3 дроби |
a1 |
, |
a2 |
, |
a3 |
. Найти, какая из трех дробей наибольшая. |
|
b1 |
b2 |
b3 |
|||||
|
|
|
|
21.Определить, имеет ли решение система {dxax eyby==cf . Если решение есть, найти
значение x и y.
22.Определить, при каких значениях х и y векторы A=a1i+a2j+xk и B=yi+b2j+b3k коллинеарны и какой из векторов короче.
23.Проверить коллинеарность векторов A=(a1, a2, a3) и B=(b1, b2, b3). Установить, какой из них длиннее и во сколько раз.
24.Даны координаты вершин двух треугольников ABC и DFG: A(a1,a2), B(b1,b2), C(c1,c2), D(d1,d2), F(f1,f2), G(g1,g2). Определить, периметр какого треугольника больше.
25.Даны две прямые y=a1×x+c1 и y=a2×x+c2. Определить условие
перпендикулярности прямых, и если оно не выполнятся, найти угол между ними.
26.Задана показательная функция y=ax. Проверить, является ли функция возрастающей ( при a>1)или убывающей (при 0 £ a £ 1). Задана функция
обратной пропорциональности y= kx . Определить, в каких координатных углах расположены ветви гиперболы.
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
9 |
||||||
|
|
|
Лабораторная работа №3. |
|
|
||
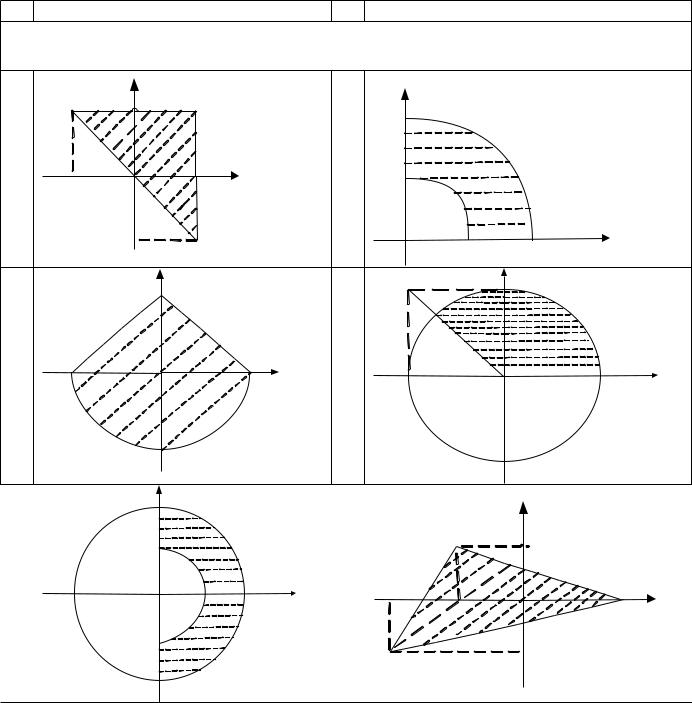
Тема «Условный оператор в С++. Вычисление значения функции, проверка |
|||||||
|
попадания точки в область на плоскости» |
|
|||||
Цель работы : Изучение условного оператора в языке С++[1, с. 59-73]. |
|
||||||
Задание. Составить алгоритм и написать программу для решения задачи |
|||||||
согласно своему варианту (табл. 3.1). |
|
|
|
|
|||
Таблица 3.1. Варианты заданий к лабораторной работе №3 |
|
||||||
№ |
Условие задачи |
№ |
Условие задачи |
|
|||
Даны вещественные числа x и y. Определить принадлежит ли точка с координатами |
|||||||
(x; y) заштрихованной части плоскости. |
|
|
|
|
|||
1 |
Y |
|
|
2 |
Y |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
1 |
X |
0.5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
X |
|
|
|
|
|
0 |
0.5 |
1 |
|
3 |
Y |
|
|
4 |
Y |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
X |
-1 |
|
1 |
X |
-1 |
|
|
|
|
|||
|
|
1 |
|
|
0 |
|
|
|
-1 |
|
|
|
|
|
|
5 |
Y 2 |
|
|
6 |
|
Y |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
0 |
1 |
X |
-2 |
-1 |
|
X |
|
2 |
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
-1 |
|
|
-2 |
|
|
|
|
|
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
10 |
|||||||
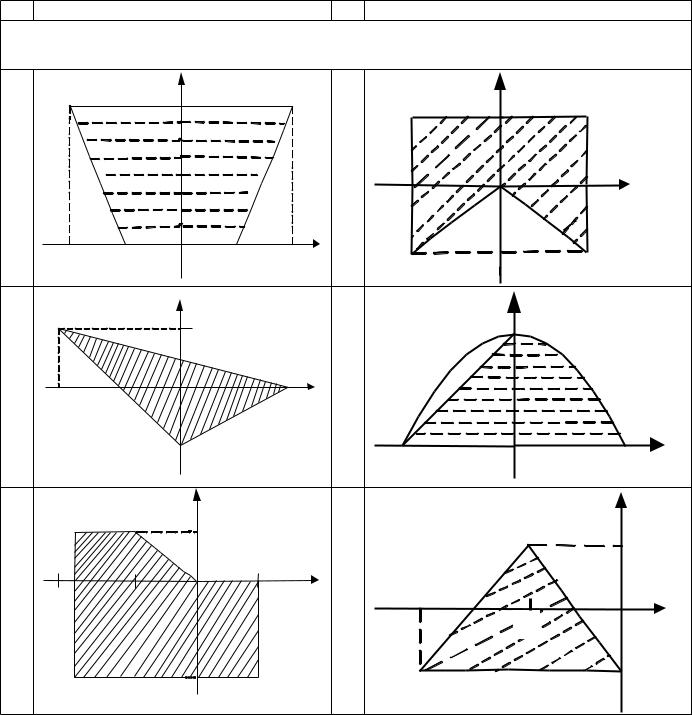
Продолжение табл. 3.1. |
|
|
|
|
|
|
||
№ |
Условие задачи |
№ |
Условие задачи |
|
||||
Даны вещественные числа x и y. Определить принадлежит ли точка с координатами |
||||||||
(x; y) заштрихованной части плоскости. |
|
|
|
|
||||
7 |
Y |
2 |
|
8 |
Y |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
1 |
X |
|
|
|
|
X |
|
|
|
|
-2 |
-1 |
0 |
1 |
2 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
Y |
|
10 |
Y |
1 |
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
y=1-x2 |
|||
|
|
|
|
|
|
|
||
|
|
|
|
X |
|
|
|
|
-2 |
|
0 |
|
2 |
|
|
|
|
|
|
-1 |
|
-1 |
|
0 |
|
1 |
|
|
|
|
|
|
X |
||
|
|
|
|
|
|
|
||
11 |
|
Y |
|
12 |
|
|
Y |
|
|
|
1 |
|
|
|
|
|
1 |
-2 |
-1 |
|
1 |
X |
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-1 |
|
X |
|
|
-2 |
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
|
11 |
||||||||
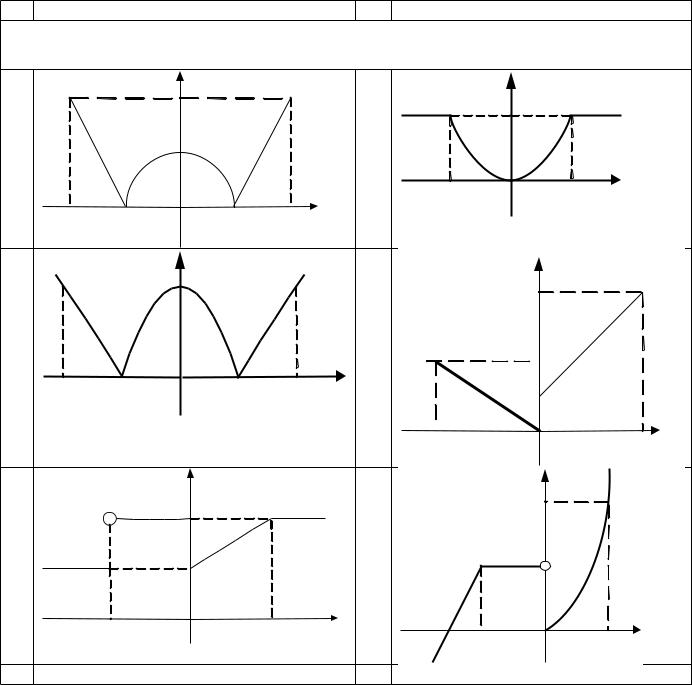
Продолжение табл. 3.1. |
|
|
|
|
|
|
|
|
||
№ |
Условие задачи |
|
№ |
Условие задачи |
|
|
||||
Дано вещественное число а. Для функции y=f(x), график которой приведен ниже |
|
|||||||||
вычислить f(а). |
|
|
|
|
|
|
|
|
|
|
13 |
Y |
|
|
|
14 |
Y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x2+y2=4 |
|
|
y=x2 |
X |
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X |
-1 |
0 |
|
1 |
|
|
-5 |
-2 |
0 |
2 |
5 |
|
|
|
|
|
|
15 |
Y |
1 |
|
|
16 |
Y |
4 |
|
|
|
|
y=1-x2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
2 |
|
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
-3 |
|
0 |
|
3 |
X |
|
|
|
|
|
|
|
|
|||
17 |
|
Y |
|
|
18 |
Y |
4 |
2 |
|
|
|
2 |
|
|
y=x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
X |
|
|
-1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
-3 |
-2 |
0 |
1 |
2 |
|
|||
|
|
|
|
|
|
|||||
19 |
|
|
|
|
20 |
|
|
|
|
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
12 |
|||||||
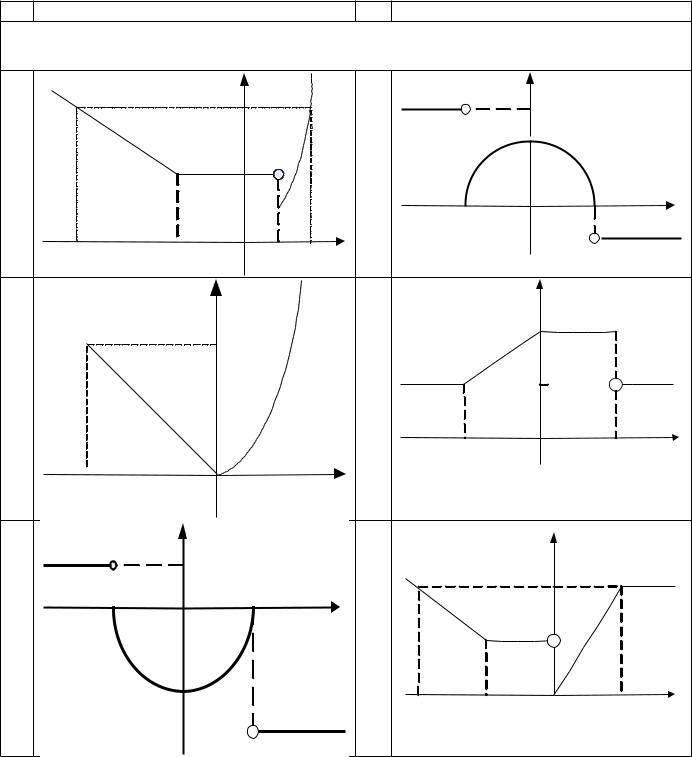
Продолжение табл. 3.1. |
|
|
|
|
|
|
|
|
№ |
Условие задачи |
|
|
№ |
Условие задачи |
|
||
Дано вещественное число а. Для функции y=f(x), график которой приведен ниже |
||||||||
вычислить f(а). |
|
|
|
|
|
|
|
|
21 |
Y |
4 |
|
2 |
22 |
|
Y |
|
|
y=x |
|
|
|
||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
X |
|
|
|
|
X |
-2 |
|
2 |
|
-5 |
|
|
|
|
|
-1 |
|
|
-2 |
0 |
1 |
2 |
|
|
|
||
|
|
|
|
|||||
23 |
Y |
|
|
|
24 |
|
Y |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=x2 |
|
|
1 |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
X |
-1 |
|
0 |
1 |
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
||
-3 |
|
|
|
|
|
|
|
|
25 |
Y |
|
|
|
26 |
|
Y |
|
|
1 |
|
X |
|
|
|
2 |
|
|
0 |
|
|
|
|
|
||
-2 |
2 |
|
|
|
|
|
||
-1 |
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
-2 |
-1 |
0 |
1 |
|
-3 |
|
|
|
|
|
|
|
Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Лабораторные работы «Программирование на С++» |
13 |
Лабораторная работа №4. |
|
Тема «Программирование циклических вычислительных процессов с |
|
варьируемым параметром цикла» |
|
Цель работы : Изучение операторов цикла в языке С++ [1, с. 77-82].
Задание. Составить алгоритм решения задачи согласно своему варианту. В отчете предоставить три программы с разными операторами цикла (do ...while, while, for). В алгоритме и программе массивов не использовать.
Варианты заданий
1. Вычислить значения у, соответствующие каждому значению х ( xn≤x≤xk ,
шаг изменения x равен dx) по формуле у= 3 a−x2 ln 2 a2 x4 . 2
Вычислить всех сумму, произведение ненулевых и количество отрицательных значений у. На экран выводить каждую третью пару значений x и y Контрольный расчёт провести при a=2.17, xn=-1.5, xk=0.5, dx=0.2..
2. Вычислить значения z, соответствующие каждому значению х ( xn≤x≤xk ,
шаг изменения x равен dx) по формуле z= |
3 x4 ax |
. Определить |
|
sin 13,2 x |
|||
|
|
среднее арифметическое вычисленных z. Найти количество z>a. На экран выводить каждую четвертую пару значений x и z. Контрольный расчёт провести при a=5.27, xn=1, xk=10, dx=1.
3. Вычислить значения t, соответствующие каждому значению х ( xn≤x≤xk ,
шаг изменения x равен dx) по формуле |
t= |
a−b 3 x |
. Определить |
cos b sin a −12 |
F =∏∑tt . На экран выводить каждую вторую пару значений x и t.
Контрольный расчёт провести при a=3.5, b=6.8, xn=-3, xk=3, dx=0.5
4. Вычислить значения t, соответствующие каждому значению х ( xn≤x≤xk ,
шаг изменения x равен dx) по формуле t= |
3 ax |
. Вычислить сумму |
5 cos a ex |
положительных значений t, произведение отрицательных t, количество всех значений t. На экран выводить каждую вторую пару значений x и t. Контрольный расчёт провести при a=1.23, xn=-0.5, xk=0.5, dx=0.1.
5. Вычислить значения z, соответствующие каждому значению х ( xn≤x≤xk ,
|
3 |
1 |
|
|
|
шаг изменения x равен dx) по формуле z= |
|
|
|
|
. Вычислить |
7 x2 |
|
||||
|
|
2 |
3 |
||
|
14,5 log a |
||||
