3.2. Методы определения ошибки устройства, вызванной действием одной первичной ошибки

Ошибка устройства вызывается действием целого ряда погрешностей, которые связаны с ограниченной точностью изготовления и функционирования элементов устройства, в том числе и преобразователей информации (ПИ). Такие погрешности называются первичными ошибками.

В идеальном устройстве связь между выходной и входной величинами является заданной математической зависимостью. В качестве входных величин могут выступать параметры элементов устройства.

Различают три основные варианта зависимостей, реализуемых в вычислительных устройствах.

1. Зависимость выходной координаты от входной координатыможет быть задана в конечной форме. Например, для инвертирующего усилителя.

2. Эта зависимость может быть дифференциальной и иметь вид . Например, для интегратора эта зависимость имеет вид

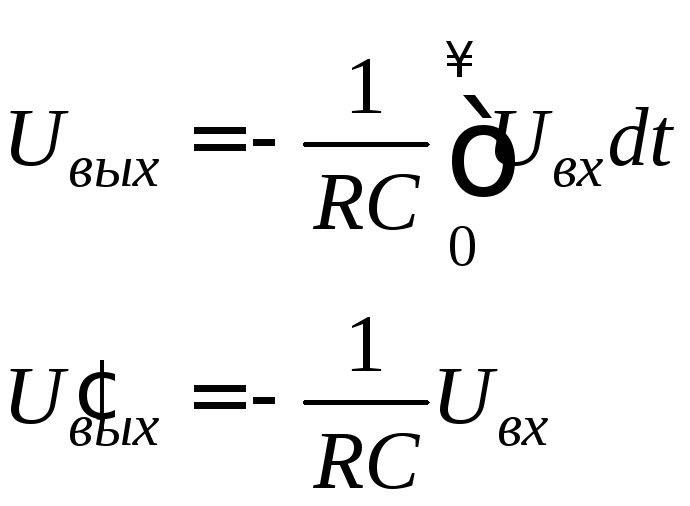
3. Зависимость выходной координаты от входной может быть задана с помощью некоторого дифференциального уравнения или же системы дифференциальных уравнений .

В действительности устройств, воспроизводящих с абсолютной точностью указанные зависимости, не существует, т.к. в любом устройстве присутствуют первичные ошибки.

Для преобразователей информации чаще всего осуществляется связь между входной и выходной координатой в виде конечной формы. Согласно определению, ошибка в этом случае равна , где– реальная выходная величина,– идеальная выходная величина.

Величины, характеризующие элементы реального устройства имеют значения, отличные от расчетных значений и равны.

представляют собой первичные ошибки устройства. Как правило, они малы. Тогда выражение для можно записать так:

.

Разложив правую часть выражения для в ряд по степениполучающегося из формулы Тэйлора

и отбросив слагаемые, содержащие эти величины в степени выше первой (из-за малости ), т.е. линеаризуем правую часть выражение дляпо величинамполучим

.

Это слагаемое представляет собой ошибку устройства, вызванную действием одной первичной ошибки, и носит название абсолютной функции чувствительности.

Относительная функция чувствительности определяется выражением

.

3.3. Методы суммирования случайных ошибок

С точностью до малых величин второго порядка малости ошибка устройства, возникающая от совместного действия нескольких первичных ошибок, есть линейная функция отдельных ошибок , каждая из которых вызывается только одной первичной ошибкой

.

Принцип независимости действия первичных ошибок применим, если все первичные ошибки малы, и можно пренебречь малыми величинами второго порядка малости.

Он применим также, если при разложении в степенной ряд по величинамвсе смешанные частые производные равны нулю.

Частные производные еще называют коэффициентами чувствительности по данному параметру.

Если первичные ошибки не зависят одна от другой, то полная погрешность на выходе устройства является результатом действия (функцией) первичных ошибок. Существуют следующие методы расчета суммарных (накопленных) ошибок:

- максимума-минимума;

- квадратичного суммирования:

- статического суммирования (теоретико-вероятностный метод).

По методу максимума-минимума полную ошибку находят арифметическим суммированием предельных значений всех ошибок:

,

при этом все положительные оценки складываются отдельно, все отрицательные – отдельно.

Этот метод дает завышенные значения суммарных ошибок (за счет действия случайных ошибок).

По методу квадратичного сложения значения всех ошибок суммируются квадратично, т.е. квадратный корень из суммы их квадратов. Результат расчетов по этому методу при наличии систематических ошибок дает заниженное значение.

По теоретико-вероятностному методу осуществляется:

а) алгебраическое суммирование математических ожиданий случайных и систематических составляющих ошибок:

,

.

б) квадратичное суммирование среднеквадратических значений случайных ошибок :

,

где – ошибка на выходе устройства, вызванная действием одной первичной ошибки. При этом предполагается, что первичные случайные ошибки взаимонезависимы.

в) закон распределения погрешности равен композиции законов составляющих погрешностей.

Теоретико-вероятностный метод дает наиболее точные результаты.

Преобразователь имеет инструментальную ошибку, которая, как правило, определяется нормальным законом распределения, т.к. содержит большое число составляющих погрешностей. Эти погрешности, при правильной технологии, дают нормальный закон (нет доминирующих погрешностей), и ошибку квантования – с равновероятностным законом распределения (см. рис. 3.2).

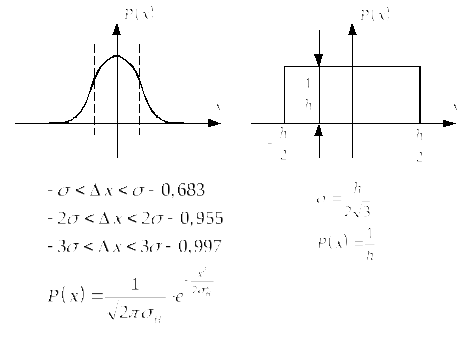
Рис. 3.2. Нормальный и равновероятный закон распределения.

Литература:

1. Д.А. Браславский, В.В. Петров, «Точность измерительных устройств», Москва, Машиностроение, 1976г.

2. Э.И. Соренков, А.И. Телегина, А.С. Шаталов, «Точность измерительных устройств», Москва, Машиностроение.

3. А.С. Бруевич, Б.Г. Постухов «Основы счетно-решающих устройств», 1964г.

4. http://www.eltech.spb.ru/pdf/A_D/2.pdf