2.1.2. Определение частоты квантования с помощью интерполяционного многочлена Лагранжа

Для медленно меняющихся монотонных функций нашёл широкое распространение метод определения частоты квантования и восстановления с помощью интерполяционного многочлена Лагранжа.

На практике нашли применение полиномы нулевого, первого и второго порядка (ступенчатая, линейная и параболическая аппроксимации).

Сущность метода интерполирования сводится к следующему: требуется построить полином степени, который вданных точках (не совпадающих друг с другом)принимал бы соответствующие известные значения:

.

Задача состоит в определении коэффициентов полинома

.

В результате получается система из линейных уравнений снеизвестным.

Решение её может быть найдено в форме Лагранжа (интерполяционная формула Лагранжа)

.

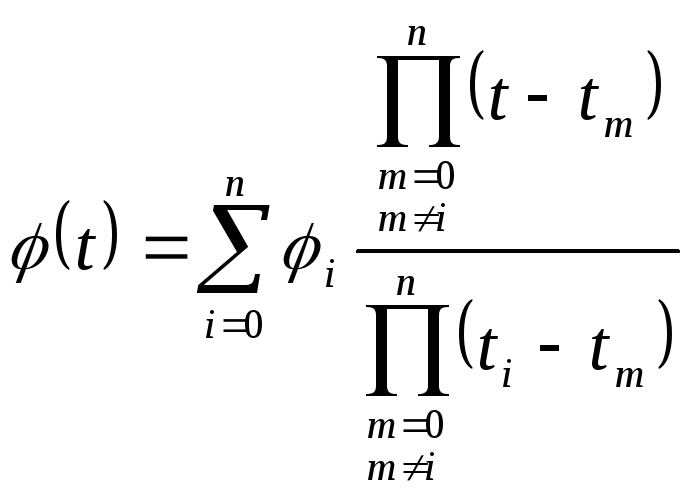Если обозначить , то погрешность аппроксимации запишется в виде остаточного члена интерполяционной формулы

.

В частности при линейной интерполяции выражение для погрешности можно определить исходя из рис. 2.4.

При ,.

Введём обозначение , тогда

.

Подставим значение и А в формулу для:

.

Рис. 2.4. Определение погрешности при линейной интерполяции.

Для определения предельной (максимальной) погрешности , необходимо определить интервал, где ошибка максимальна, для чего необходимо взять производнуюи приравнять её к нулю, т.е. получим

,

.

Следовательно

.

Подставим полученное значение в формулу остаточного члена ряда получим

.

Данное выражение позволяет определить величину интервала квантования по времени , при которой погрешность аппроксимации не будет превышать допустимой величины

.

Для примера выбора частоты квантования для медленно меняющейся функции , гдев таблице 2.1 представлены выбранные частоты квантования по теореме Котельникова и по интерполяционному многочлену Лагранжа с заданной величиной погрешности.

Таблица 2.1. Частоты квантования.

Заданная погрешность		5	1	0.5	0.1	0.05
По Котельникову	Гц	80.9	2021.6	8077.8	195405	705979
По Лагранжу при	Гц	1.59	3.55	5	11.2	15.9

Анализ таблицы показывает, что для медленно меняющихся функций некорректное применение теоремы Котельникова приводит к завышению частоты квантования при точности 0,05% примерно в 37000 раз.

2.2. Квантование по уровню

Квантование по уровню сводится к представлению текущих значений непрерывно изменяющегося сигнала конечным числом уровней.

При квантовании по уровню сигнал представляется приближенными значениями, т.е. непрерывно изменяющаяся величина представляется ступенчатой функцией(см. рис. 2.5).

Рис. 2.5. Квантованная по уровню функция .

Интервал между соседними уровнями квантования называется шагом квантования , где– единица младшего разряда (ЕМР – в русскоязычной литературе,LSB – в иностранной). Если , то квантование называется равномерным.

Амплитудная характеристика устройства, осуществляющего равномерное квантование, имеет вид, представленный на рис. 2.6.

Рис. 2.6. Амплитудная характеристика квантователя

при равномерном квантовании.

Шаг квантования по уровню, в сущности, определяет разрешающую способность преобразователя.

При равномерном квантовании непрерывной величины весь диапазон ее измененияразбивают наравных частей. При этом шаг квантования определяется следующим соотношением

.

Для квантованного сигнала характерно наличие скачков на величинув момент, когда непрерывный сигналпроходит уровень срабатывания квантователя. Ошибка квантования по уровню имеет вид –.

Ошибка квантования имеет разные значения при смещенном и несмещенном квантовании по уровню одной и той же функции (см. рис. 2.7).

При несмещенном квантовании, максимальная ошибка квантования определяется разностью между и, и нигде не превышает ±.

.

Рис. 2.7. Ошибка квантования по уровню

при смещенном и несмещенном квантовании.

При смещенном квантовании ошибка будет определяться следующим образом:

Найдем среднеквадратическую ошибку, обусловленную квантованием сигнала по уровню.

Отметим, что для того, чтобы шум квантования был не коррелирован с исходным сигналом, необходимо выбрать h порядка среднеквадратического значения исходного сигнала, тогда плотность вероятности шума квантования является равномерной в пределах шага квантования h.

Так как , то даже небольшое изменениеоказывается соизмеримым с. Поэтому полагают, что в момент отсчета величинас равной вероятностью может принимать любое значение в пределахвблизи одного из уровней квантования. Это означает, что для ошибкив точке отсчета можно принять равновероятный закон распределения вероятности (см. рис. 2.8).

Т.к. площадь подынтегральной кривой равна 1, то вероятность определяется следующим выражением

.

Дисперсия ошибки квантования по уровню определяется по формуле

.

Рис. 2.8. Равновероятный закон распределения вероятности

ошибки квантования по уровню.

С учетом выражения для равновероятного закона распределения

.

Отсюда

.

Среднеквадратическая погрешность квантования в раз меньше предельной ошибки квантования.

Литература:

1. О.Н. Новосеров, А.Ф. Фомин «Основы теории и расчёта информационно измерительных систем».

2. П.И. Пенин «Системы передачи цифровой информации» Сов.радио, М. 1976.

3. http://www.eltech.spb.ru/pdf/A_D/2.pdf