2.1.1. Определение частоты квантования по теореме Котельникова

Теорема Котельникова (в иностранной литературе – теорема отсчётов или теорема Найквиста) формулируется следующим образом.

1-ая теорема.

Любую функцию , имеющую ограниченный спектр частот от нуля дои наблюдаемую бесконечное времяможно представить в виде

,

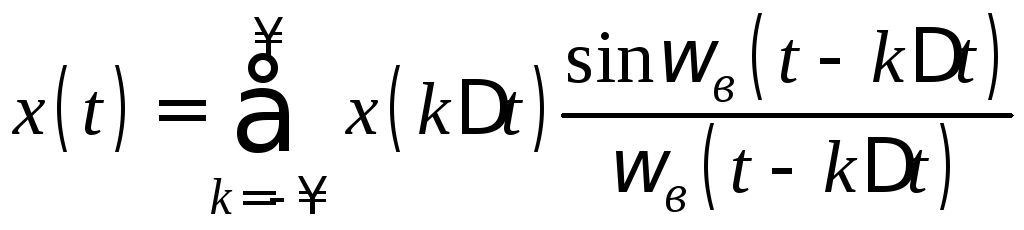где – целое число,– значение функции вмомент времени,.

2-ая теорема.

Любую функцию , имеющую ограниченный спектр частот от нуля дои наблюдаемую бесконечное времяможно представить с любой степенью точностипри помощи чисел, следующих друг за другом через равные интервалы времени.

Из первой теоремы следует, что функция , имеющая ограниченный спектр частот, может быть представлена в виде бесконечной суммы, каждое слагаемое которой выражается функцией видаи отличается от остальных слагаемых значениями амплитуди временным сдвигом.

Функция

называется функцией Котельникова или функцией отсчётов.

Функция отсчётов в моменты отсчёта, то естьпринимает максимальное значение, равное единице и имеет вид, представленный на рис. 2.1.

Функция , в соответствии с 1-й теоремой, в каждый момент времениопределяется только одним-ым слагаемым, так как все остальные слагаемые в этот момент времени обращаются в нуль (см. рис.2.2).

Для полного восстановления непрерывной функции по значениям её отсчётов необходимо просуммировать бесконечное множество членов ряда.

Рис. 2.1. Функция отсчётов .

Рис. 2.2. Функция , в соответствии с 1-й теоремой.

На практике все исследуемые процессы обычно ограничены во времени и как следствие из этого не могут иметь ограниченный спектр, при этом при применении теоремы Котельникова возникают погрешности представления реальных сигналов (две составляющих).

Первая составляющая.

Если у сообщения длительностью ограничить спектр на частоте, то в соответствии с теоремой Котельникова можно образовать число отсчетов, равное

.

В этом случае будет содержать конечное число членов и, следовательно, представление непрерывной функции таким рядом будет неточным:

Оценим качественно погрешность .

Поскольку функция вида обращается в нуль во всех точках отсчётов, кроме точки, то в-ой точке значенияибудут совпадать, то есть.

Рис. 2.3. График погрешности .

Погрешность достигает наибольшей величины где-то в середине интервала между отсчётами. Кроме того, поскольку в образовании значений функции в середине интервалаучаствует большее число слагаемых, то величина погрешностивозрастает к концам интервала(см. рис. 2.3).

Среднеквадратическую ошибку, вызванную указанной погрешностью можно определить соотношением:

,

где - полная энергия,- та часть энергии сигнала, которая не учитывается за счёт конечного числа членов суммирования.

Вторая составляющая.

Среднеквадратическая ошибка, связанная с ограничениями энергетического спектра стационарного случайного процесса граничной частотой , определяется выражением:

.

–энергетический спектр, равный , где– модуль амплитудного спектра, усреднённый по множеству реализаций.

Общая среднеквадратическая ошибка при дискретизации непрерывного сообщения конечной длительности, с учетом того, что , может быть определена выражением

.

Восстановление непрерывного сообщения по его отсчётам должно выполняться в соответствии с теоремой 1. Эта процедура может быть выполнена двумя способами:

- фильтрационным, с применением аналогового фильтра;

- с помощью специальных интерполяторов или универсальных ЭЦВМ.

Восстановление фильтрационным способом физически не реализуемо.

Восстановление интерполяционным способом, требует большого объёма памяти машины, и получить на выходе исходную функцию можно только после прохождения всего процесса , то есть имеет задержку на, что не даёт возможности работы в реальном масштабе времени.

Для стационарных сигналов с равномерным спектром, для которых приемлемо определять интервал квантования по теореме Котельникова, восстановить функцию можно, применив ступенчатую, линейную или параболическую интерполяцию. Тогда при заданной ошибке нужно увеличить частоту квантования или уменьшать интервал квантования согласно следующим выражениям:

- при ступенчатой интерполяции ;

- при линейной интерполяции ;

- при параболической интерполяции ;

где ,– допустимая относительная погрешность равномерного приближения

,

причём

.

Методика инженерного расчёта необходимого интервала дискретизации при выбранном виде интерполяции для сообщений с быстро спадающим спектром следующая:

- по требуемой точности дискретизации илии выражениюдля энергетического спектра случайного процесса, описывающего рассматриваемый класс непрерывных сообщений, определяют верхнюю граничную частоту спектра;

- по частоте находят предельный интервал дискретизации, соответствующий 2-й теореме Котельникова;

- для выбранного вида интерполяции рассчитывают необходимый интервал дискретизации, используя приведенные выше формулы.

В инженерном приложении можно приять, что спектр является медленно спадающим, если уменьшение спектральной плотности происходит медленнее, чем изменяется величина .