7.3. Циклический преобразователь с промежуточным преобразованием в фазу и временной интервал

В общем виде гониометрический фазовращатель (ФВ) представляет собой систему из N элементов, модулирующих по закону, близком к гармоническому -систему из-фазных напряжений -.

Система модулирующих элементов построена таким образом, что фазовый сдвиг модуляции двух соседних элементов отличается на .

Другими словами происходит перемножение -фазных напряжений изаконов модуляции.

После суммирования результатов этих операций получаем напряжение, модуль которого постоянен и фаза завит от угла поворота входного вала.

Запишем условие получение фазового сдвига:

где – число фаз,– глубина модуляции (амплитудной),– угол поворота вала датчика.

При выполнении операции суммирования следует иметь ввиду, что сумма равных по амплитуде векторов, образующих замкнутую систему по фазе от 0 до , равна нулю.

Проделав несложные тригонометрические преобразования, получим

,

,

.

Последние выражения отражают формирование фазового сдвига при идеальных условиях, т.е. при гармоническом законе огибающей в функции и гармонических сигналах с расщепленной фазой.

На практике гармонический закон модуляции как правило не имеет места, а фазорасщепленным сигналам часть придают прямоугольную форму.

Модулирующие элементы могут быть самой физической природы – СКВТ, индуктивные, оптические, емкостные фазовращатели.

Несмотря на многообразие фазовращателей, метод обработки информации во всех преобразователях примерно одинаков.

7.4. Фазовращатель на основе вращающихся трансформаторов (вт, сквт)

В многочисленных схемах построения фазовращателя (ФВ) на ВТ или СКВТ используются два основных принципа:

а) создание потока возбуждения в виде вращающегося кругового магнитного поля

б) суммирование выходных напряжений СКВТ с помощью фазосдвигающих -цепочек, система с пульсирующем полем.

Первые из них получили название ФА с вращающимся полем, а вторые – фазовращатели с пульсирующим полем.

7.4.1. Схема фазовращателя с вращающимся полем

Статорные катушки питаются двухфазным током

.

Токи, протекающие по катушкам статора создают взаимно-перпендикулярные магнитные поля, пересекающие витки роторной катушки. ЭДС, индуцируема в роторной обмотке равна сумме ЭДС от двух статорных обмоток

,

где

–

коэффициенты взаимоиндукции между роторной и статорной обмотками.

Рис. 7.6. Фазовращатель с вращающимся полем.

Таким образом получим

или

Из последнего выражения следует, что при изменении угла поворота роторной катушки соответственно изменяется фаза ЭДС в пределах. Амплитуда ЭДСне зависит от сдвига фазы.

Следует также отметить, что вращающиеся трансформаторы в режиме питания вращающим полем имеют низкоомное выходное сопротивление.

Основным источником погрешности такого фазовращателя является неортогональность и неравенство амплитуд токов питания, т.е. погрешность квадратурного питания.

Если - отклонение питающих напряжений от квадратуры,угол поворота ротора СКВТ,- различие в амплитудах питающих токов, то ошибка по фазе от неортогональности питающих напряжений приближенно может быть определена

и имеет график

Неравенство амплитуд питающих токов приводит к погрешности по фазе

и ее график имеет вид

Существенно уменьшить влияние ошибок от неортогональности и неравенства модулей векторов питающих напряжений на величинуможно, применив фильтр обратной последовательности.

Суть метода состоит в следующем. Анализ погрешностей электрических машин при использовании вращающегося магнитного поля удобно производить методом симметричных составляющих, разбивающем замкнутую искаженную систему векторов на ряд идеальных систем, параметры которых зависят от степени отклонения исходной системы от идеальной. Определив характеристики новых систем, можно рассматривать их влияние на электрическую машину раздельно, используя метод наложения.

Согласно методу симметричных составляющих два вектора и, в общем случае неравные и неортогональные, можно заменить двумя системами равных по модулю и ортогональных векторови.

Для этого должны быть выдержаны следующие соотношения.

Из этих соотношений определяем зависимости векторов новой системы от векторов исходной:

Используем разложение системы векторов по методу симметричных составляющих:

Обратим внимание на то, что система с индексом 1 имеет следование фаз такое же, как и исходная, а с индексом 2 – обратное следование.

С помощью этого метода можно провести анализ работы ФВ на ВТ с квадратурным питающим напряжением.

Исходя из относительного неравенства амплитуд и отклонения от ортогональностипитающих напряжений, определим прямую и обратную системы напряжений.

Идеальный выходной сигнал фазовращателя представим как вырабатываемый системой с прямой последовательностью, система с обратной последовательностью возбуждает на выходе фазовращателя сигнал, обуславливающий погрешность.

Сумма от выходных сигналов обоих систем даёт реальный сигнал от исходной системы векторов.

Действие системы обратной последовательности можно в значительной степени компенсировать при использовании так называемого фильтра обратной последовательности (ФОП), который состоит из фазосдвигающей цепи, сдвигающий выходное напряжение ВТ на .

Схема представлена на рис. 7.7.

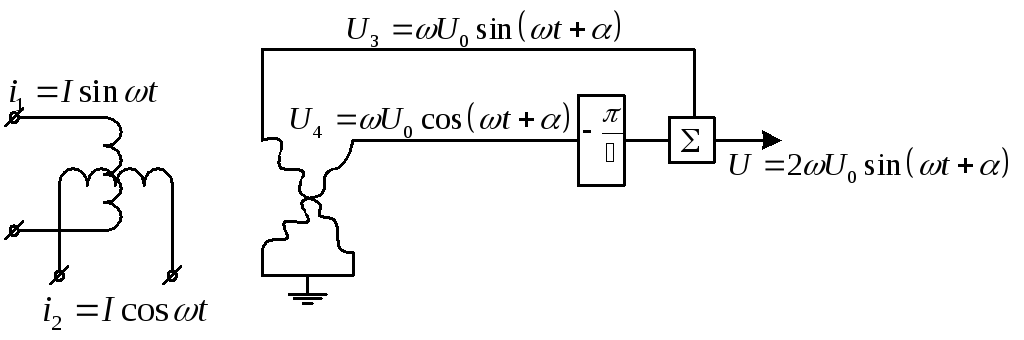
Рис. 7.7. Фазовращатель с ФОП.

В выходном сигнале отсутствуют составляющие от системы обратной последовательности, так как они компенсируют друг друга.

При применении ФОП устраняется и значительная часть погрешностей самого ВТ – неидеальность магнитной системы, несинусоидальность коэффициента взаимной индукции и т.п.

Точность увеличивается от 2 до 10 раз.